5 Équitabilité

L’équitabilité mesure l’écart entre la distribution observée et une distribution uniforme.

L’indice de Pielou est la mesure d’équitabilité la plus connue. Il a été généralisé pour permettre de pondérer plus ou moins les espèces rares, de la même façon que l’entropie HCDT.

La régularité d’une distribution est une notion intuitivement assez simple : la faiblesse de l’écart entre la distribution réelle et une distribution parfaitement régulière (Lloyd et Ghelardi 1964), vérifiant \(p_s={1}/{S}\). Des difficultés apparaissent quand il s’agit de comparer l’équitabilité de communautés de richesses différentes. L’approche axiomatique est présentée, puis les différents indices de la littérature et enfin la généralisation de l’indice de Pielou, en cohérence avec l’entropie HCDT.

5.1 Approche axiomatique

Une approche axiomatique a été développée par la littérature, revue par Jost (2010b) ou Tuomisto (2012) Les propriétés fondamentales sont les critères de Dalton (1920) :

• L’équitabilité augmente quand un individu est transféré d’une espèce fréquente à une espèce rare ;
• L’équitabilité diminue quand une espèce rare est ajoutée ;
• Invariance d’échelle : l’équitabilité ne dépend que des fréquences, pas des abondances absolues.

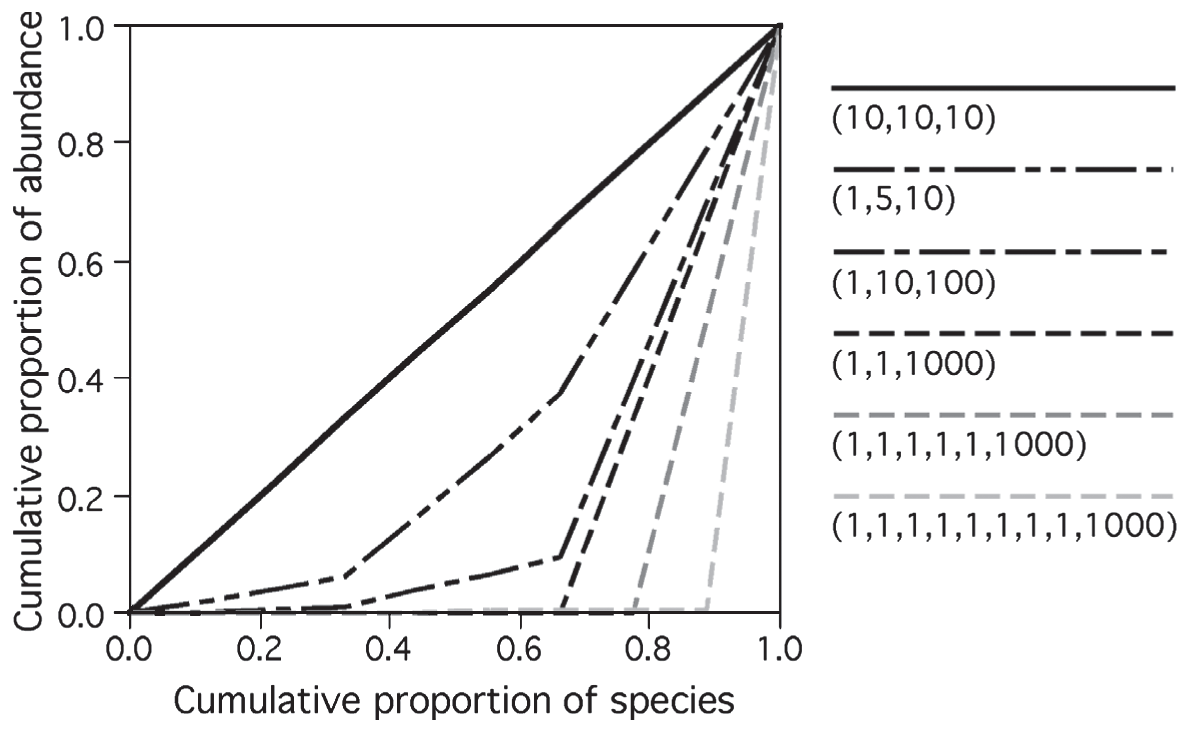
Figure 5.1: Tuomisto2012

Un critère supplémentaire établi par B. Smith et Wilson (1996), complété par Gosselin (2001) est la compatibilité avec la courbe de Lorenz (1905), construite en classant les espèces de la moins fréquente à la plus fréquente, et en traçant le cumul des fréquences en fonction du rang (figure 5.1, Tuomisto 2012) : une communauté parfaitement équitable est représentée par la bissectrice. La surface entre la courbe réelle et la bissectrice est très utilisée en économie pour mesurer l’inégalité sous le nom d’“indice de Gini” (Gini 1912; Ceriani et Verme 2012) :

• Compatibilité avec la courbe de Lorenz : l’équitabilité augmente pour une communauté si sa courbe de Lorenz est plus proche de la bissectrice. Si les courbes de deux communautés se croisent, l’ordre de leurs équitabilités est imprévisible.

Ce critère est remis en cause par Ricotta (2004b) : il est incompatible (Routledge 1983) avec le critère de continuité retenu pour les mesures de diversité : l’introduction d’une espèce supplémentaire avec une probabilité infinitésimale peut modifier considérablement l’équitabilité.

L’invariance par réplication est une propriété nécessaire (mais pas suffisante) à la compatibilité avec la courbe de Lorenz (Ricotta 2004b) :

• Invariance par réplication : l’équitabilité ne change pas si chaque espèce est remplacée par plusieurs nouvelles espèces ayant la même abondance.

Cette propriété est retenue par Tuomisto mais rejetée par Jost comme par Ricotta et d’autres. L’argumentation de Jost est la plus convaincante : une communauté d’une richesse donnée dans laquelle tous les individus (à l’exception d’un nombre négligeable) sont concentrés dans une seule espèce atteint le niveau minimum d’équitabilité. Si elle est dupliquée, les individus seront répartis dans deux espèces et non une : la nouvelle communauté n’atteindra pas le niveau minimum d’équitabilité, il est donc souhaitable que la mesure d’équitabilité augmente.

5.2 Indice classiques

5.2.1 Indice de Bulla

L’indice d’équitabilité de Bulla (1994) respecte les critères de Smith et Wilson : \[\begin{equation} \tag{5.1} O = \sum_s{\min(p_s,\frac{1}{S})}. \end{equation}\]

Il mesure l’écart entre la distribution réelle et une distribution parfaitement équitable. Bulla le normalise pour qu’il soit compris entre 0 et 1 : \[\begin{equation} \tag{5.2} E_O = \frac{O - \min{O}}{1 - \min{O}}. \end{equation}\]

La valeur minimale de \(O\) est \({1}/{S}\). Bulla considère que ce n’est pas le cas si les effectifs sont entiers et fournit une valeur exacte dépendant du nombre d’espèces.

5.2.2 Indice de Gini

L’indice de Gini est le double de la surface comprise entre la courbe de Lorenz et la bissectrice (figure 5.1).

5.2.3 Rapports de moyennes

Taillie (1979) propose le rapport de la moyenne géométrique ou de la moyenne harmonique à la moyenne arithmétique des probabilités.

5.2.4 Ratios de Hill

Hill (1973) utilise les rapports entre nombres effectifs d’espèces d’ordres différents comme mesure d’équitabilité. \(E_{1,0} = {^{1}\!D}/{^{0}\!D}\) avait déjà été proposé par Sheldon (1969). Peet (1974) le normalise en retirant au numérateur et au dénominateur leur valeur minimale, c’est-à-dire 1.

La version normalisée de \(E_{2,1}\) est recommandée par Alatalo (1981).

5.2.5 Synthèse

Ricotta et al. (2001) testent ces indices sur 65 jeux de données différents pour observer leurs corrélations. Tous sont compatibles avec la courbe de Lorenz. Ils concluent que les indices se répartissent en deux groupes : la plupart sont sensibles aux abondances relatives des espèces rares. \(E_{\infty,0}\) et, dans une moindre mesure, \(E_{2,0}\) sont plus sensibles aux espèces fréquentes.

5.3 Indice alternatifs

5.3.1 Variance de la rareté

Engen (1977) définit comme mesure d’équitabilité la variance de la rareté (la fonction d’information) de l’entropie de Shannon (\(-\ln p\)) : \[\begin{equation} \tag{5.3} E_\mathit{VS} = \sum_{s}{p_s(\ln p_s)^2}-(\sum_s{p_s \ln p_s})^2. \end{equation}\]

Sa valeur est nulle si les espèces sont équiprobables.

Ricotta (2003) généralise cette mesure aux autres fonctions d’information. Toutes peuvent être utilisées :

\[\begin{equation} \tag{5.4} E_\mathit{VR} = \sum_{s}{p_s I(p_s)^2}-[\sum_s{p_s I(p_s)}]^2. \end{equation}\]

Ces mesures ne sont pas invariantes par réplication mais sont continues par rapport aux probabilités.

5.3.2 Non-spécificité

Ricotta (2004b) propose un indice fondé sur les ensembles flous, utilisant les mesures de spécificité (Yager 1992). Les espèces sont classées par probabilité décroissante. La mesure de non-spécificité utilisable comme mesure d’équitabilité est

\[\begin{equation} \tag{5.5} E_\mathit{NSp} = \sum_{s=1}^{S-1}{\frac{p_s-p_{s+1}}{s}}. \end{equation}\]

Cet indice n’est pas invariant par réplication mais est continu par rapport aux probabilités.

5.4 Indice de Pielou

Une expression de l’équitabilité est souvent donnée à partir de l’indice de Shannon (Lloyd et Ghelardi 1964; Sheldon 1969; Pielou 1966b, 1975). La valeur maximale de l’indice de Shannon est obtenue quand la distribution est parfaitement régulière. Alors : \(H_{\max}=\ln S\). On a donc défini l’indice, souvent appelé “indice de Pielou” :

\[\begin{equation} \tag{5.6} J = \frac{H}{H_{\max}} = \frac{H}{\ln S}. \end{equation}\]

\(J\) est compris entre 0 (une seule espèce a une probabilité de 1) et 1 (toutes les espèces ont la même probabilité).

5.5 Généralisation de l’indice de Pielou

5.5.1 Mendes et al. 

Mendes et al. (2008) généralisent l’indice de Pielou en remplaçant l’indice de Shannon par l’entropie de Tsallis. Ils définissent

\[\begin{equation} \tag{5.7} ^{q}\!J^{*} = \frac{^{q}\!H}{^{q}H_{\max}} = \frac{^{q}\!H}{\ln_q{S}} \end{equation}\]

et tracent des profils d’équitabilité, c’est-à-dire la valeur de \(^{q}\!J^{*}\) en fonction de \(q\). Ils observent que l’équitabilité est minimale pour une valeur particulière de \(q\) qu’ils notent \(q^*\) et montrent sur des exemples simulés que \(q^*\) diminue avec la richesse de la communauté, mais sans en explorer complètement les propriétés.

\(^{2}\!J^{*}\) est l’indice d’équitabilité dérivé de l’indice de diversité de Simpson par Hurlbert (1971).

5.5.2 Tuomisto

Tuomisto argumente en faveur d’une définition stricte de l’équitabilité (evenness en anglais, equitability pouvant être utilisé dans un sens plus large) en tant que ratio de Hill :

\[\begin{equation} \tag{5.8} ^{q}\!E = E_{q,0} = \frac{^{q}\!D}{^{0}\!D} = \frac{^{q}\!D}{S}. \end{equation}\]

L’équitabilité d’ordre \(q\) est le rapport de la diversité d’ordre \(q\) sur la richesse.

L’idée fondamentale de la notion d’équitabilité est que la mesure de la diversité doit pouvoir être partitionnée en deux composantes indépendantes : la richesse et l’équitabilité (B. Smith et Wilson 1996).

5.5.3 Jost

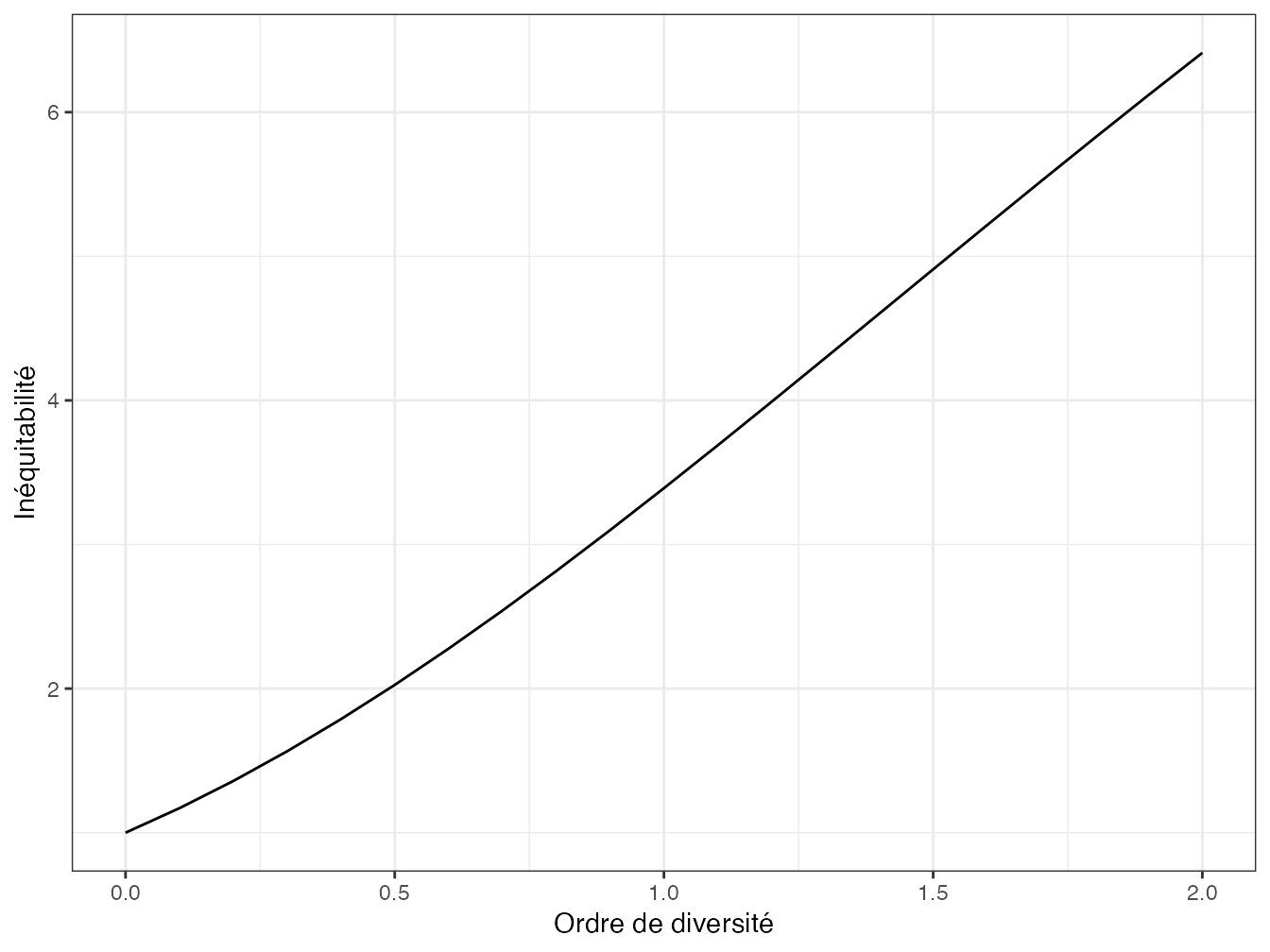
Figure 5.2: Profil d’inéquitabilité de BCI : L’inéquitabilité augmente quand on néglige de plus en plus les espèces rares. Pour q=2, la forêt de BCI est aussi inéquitable qu’une communauté de 6 espèces dans laquelle une seule serait représentée au-delà d’un nombre négligeable d’individus.

Jost (2010b) montre que l’indépendance est impossible dans le cadre de la décomposition multiplicative : si \(^{q}\!E={^{q}\!D/{S}}\), sa valeur minimale est contrainte par le nombre d’espèces, une communauté pauvre ne peut pas être aussi inéquitable qu’une communauté riche (propriété déjà montrée par Sheldon (1969) ou Alatalo (1981)). En revanche, la richesse peut être partitionnée de façon indépendante en diversité et inéquitabilité : \(S={^{q}\!D}/{^{q}\!E}\).

L’inéquitabilité \(1/{^{q}\!E}\) (figure 5.2) est un nombre effectif d’espèces : c’est la richesse d’une communauté du même niveau d’équitabilité que la communauté réelle dans laquelle tous les individus (sauf un nombre négligeable) appartiendraient à une seule espèce.

Code R pour la figure 5.2 :

# Estimation du nombre d'espèces
Ns <- colSums(BCI)
UBNs <- jackknife(AbdFreqCount(Ns), k = 1)$Nhat
# Profil
Inq <- DivPrf <- CommunityProfile(Diversity, Ns)
Inq$y <- UBNs/DivPrf$y
autoplot(Inq, xlab = "Ordre de diversité", ylab = "Inéquitabilité")

5.5.4 Synthèse

L’indice de Pielou est le plus utilisé (Tuomisto 2012) mais n’est pas invariant par réplication parce qu’il ne normalise pas une diversité mais une entropie. Il est rejeté pour cette raison (B. Smith et Wilson 1996; Tuomisto 2012) par une partie de la littérature. Jost (2010b) argumente au contraire en sa faveur : \(^{q}\!E\) dépend de la richesse et ne peut donc pas être comparé entre communautés de richesse différente. Le logarithme de \(^{q}\!E\) normalisé est une meilleure généralisation de l’indice de Pielou que celle de Mendes et al. :

\[\begin{equation} \tag{5.9} ^{q}\!J = \frac{\ln\left({^{q}\!D}\right)}{\ln S} = \frac{^{q}\!R}{\ln S}. \end{equation}\]

\(^{q}\!J\) varie entre 0 et 1 et est une transformation monotone de \(^{q}\!E\) contrairement au \(^{q}\!J^{*}\) de Mendes et al.  Il est égal au rapport de l’entropie de Rényi sur le logarithme du nombre d’espèces.

L’estimation de l’équitabilité repose lourdement sur l’estimation du nombre d’espèces, quelle que soit la valeur du paramètre \(q\). La solution la plus évidente consiste à corriger le mieux possible le biais d’estimation du nombre d’espèces et celui de l’entropie d’ordre \(q\) :

\[\begin{equation} \tag{5.10} ^q\!{\tilde{J}}= \frac{\ln\left(e_q^{^q{\tilde{H}}} \right)}{\ln\tilde{S}}. \end{equation}\]

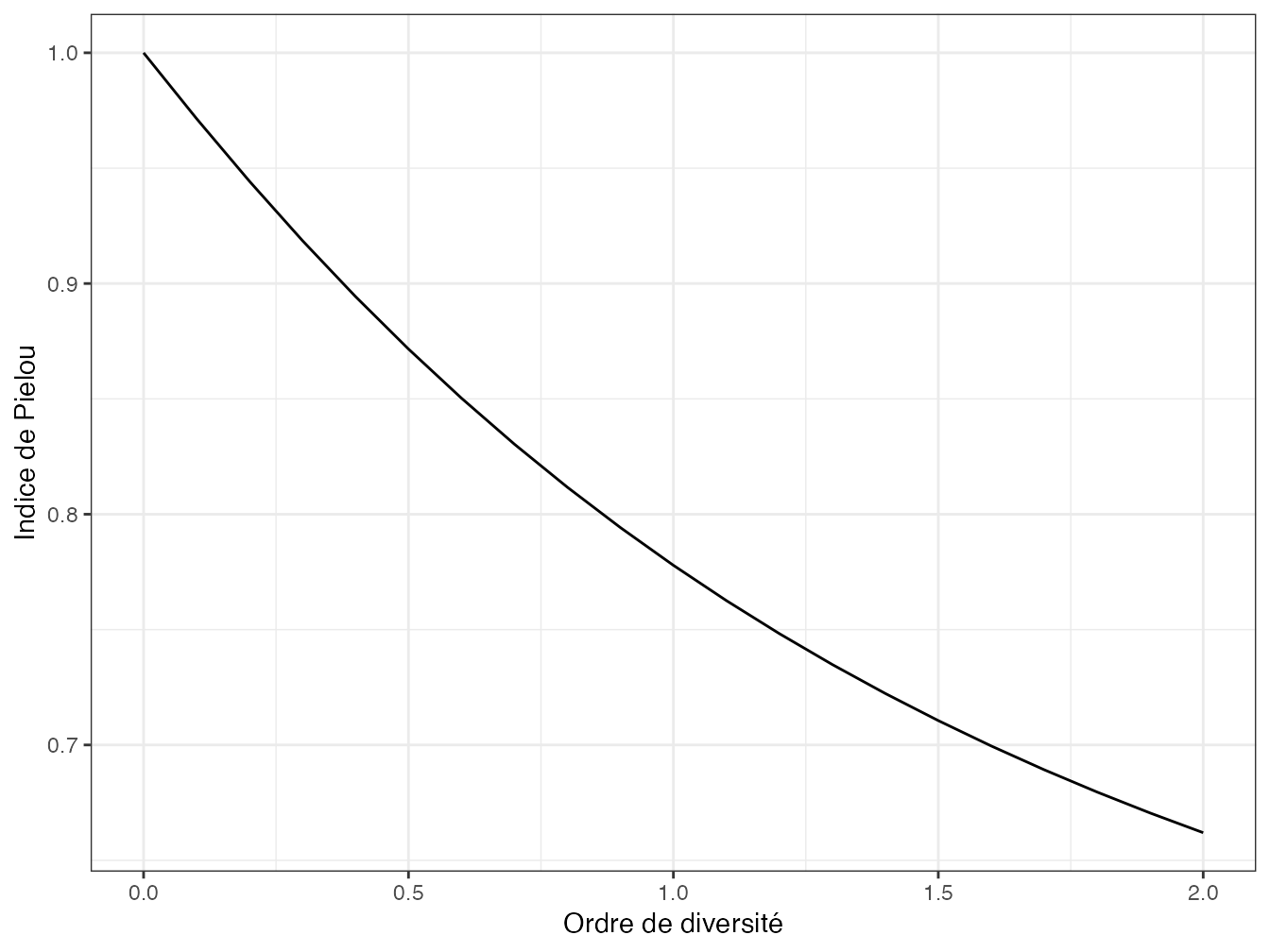
Figure 5.3: Profil d’équitabilité de BCI. L’équitabilité est ici normalisée selon Jost.

Un profil d’équitabilité calculé de cette façon est présenté en figure 5.3, représentation alternative de la figure 5.2.

Code R supplémentaire :

Inq$y <- log(DivPrf$y)/log(UBNs)
autoplot(Inq, xlab = "Ordre de diversité", ylab = "Indice de Pielou")

5.6 Relations empiriques entre richesse et équitabilité

Au-delà de la question des contraintes mathématiques entre richesse et équtabilité traitées précédemment, il s’agit ici des relations entre les deux aspects de la diversité dans des communautés réelles.

Wilsey et al. (2005) passent en revue l’argument selon lequel richesse et équitabilité seraient toujours positivement corrélés. S’il est valide, la richesse peut être considérée comme une mesure suffisante de la diversité. À partir d’inventaires de prairies, ils montrent la très faible relation entre les deux valeurs. Le suivi temporel de communautés de papillons (MacDonald, Nielsen, et Acorn 2017) met en évidence une relation négative. Les auteurs de l’étude critiquent un peu naïvement l’utilisation des nombres de Hill pour mesurer la diversité parce qu’ils confondent les effets de la richesse et de l’équitabilité : c’est justement leur but.

D’un point de vue plus théorique, DeBenedictis (1973) étudie les contraintes numériques sur l’intervalle des valeurs possibles de l’entropie de Shannon et de l’équitabilité en fonction de la richesse. Il ne prouve pas de corrélation entre ces valeurs pour des communautés réelles mais simplement un lien positif quand les échantillons sont de petite taille et l’effectif minimum de chaque espèce égal à 1 : ces contraintes se relâchent si les donnnées sont des probabilités, pouvant tendre vers 0 pour les espèces rares, ou des abondances dans de grands échantillons. Cette approche est similaire à celle de Jost (2010b), plus aboutie.

May (1975) montre que dans le cadre d’une distribution log-normale, la richesse, l’entropie de Simpson et l’équitabilité de Pielou sont positivement corrélées. Ce résultat a été étendu par G. Stirling et Wilsey (2001) aux distributions en log-séries et testé dans des communautés réelles avec des conclusions contrastées, notamment des corrélations négatives ntre richesse et équitabilité dans des communautés très riches.

Des simulations permettent de comprendre les corrélations dans des cas simples.

La figure 5.4 montre que l’entropie et l’équitabilité sont corrélées positivement à la richesse dans des communautés log-normales de même variance.

Figure 5.4: Relations entre l’entropie de Shannon (a), l’indice d’équitabilité de Pielou (b), l’entropie de Simpson (c), l’équitabilité de Hurlbert (d) et la richesse de communautés log-normales similaires (même écart-type des probabilités, seule la richesse varie).

Code R pour réaliser les figures :

# Communautés de 30 à 300 espèces
S <- 30:300
# Tirage de communautés log-normales de 10000 individus
rcl <- lapply(S, function(S) rCommunity(1, 10000, S=S))
# Richesse et Shannon
Sobs <- sapply(rcl, Richness)
H <- sapply(rcl, Shannon)
ggH <- ggplot(data.frame(S, H), aes(S, H)) +
  geom_point() + scale_x_log10() + 
  labs(x="S (échelle logarithmique)") +
  labs(tag = "a")
# Equitabilité de Pielou
J <- H/log(S)
ggJ <- ggplot(data.frame(S, J), aes(S, J)) +
  geom_point() + labs(tag = "b")
E <- sapply(rcl, Simpson)
ggE <- ggplot(data.frame(S, E), aes(S, E)) +
  geom_point() + labs(tag = "c")
J2 <- E/(1-1/S)
ggJ2 <- ggplot(data.frame(S, J2), aes(S, J2)) +
  geom_point() + labs(tag = "d")
grid.arrange(ggH, ggJ, ggE , ggJ2, ncol = 2, nrow = 2)

En revanche, dans une communauté log-normale de richesse fixe mais insuffisamment échantillonnée, les corrélations sont négatives (figure 5.5). Le sous-échantillonnage a un effet plus sévère sur la richesse que sur les entropies d’ordres supérieurs. La non observation des espèces les plus rares augmente aussi l’équitabilité.

Figure 5.5: Relations entre l’entropie de Shannon (a), l’indice d’équitabilité de Pielou (b), l’entropie de Simpson (c), l’équitabilité de Hurlbert (d) et la richesse d’échantillons de taille variable d’une même communauté log-normale.

Code R pour réaliser les figures :

# Communautés de taille 10 à 1000 individus; 300 sp.
rmc <- MetaCommunity(sapply(10:1000, function(n) rCommunity(1, n)))
# Richesse et Shannon
S <- apply(rmc$Psi, 2, Richness)
H <- apply(rmc$Psi, 2, Shannon)
ggH <- ggplot(data.frame(S, H), aes(S, H)) +
  geom_point() + scale_x_log10() + 
  labs(x="S (échelle logarithmique)") +
  labs(tag = "a")
# Equitabilité de Pielou
J <- H/log(S)
ggJ <- ggplot(data.frame(S, J), aes(S, J)) +
  geom_point() + labs(tag = "b")
E <- apply(rmc$Psi, 2, Simpson)
ggE <- ggplot(data.frame(S, E), aes(S, E)) +
  geom_point() + labs(tag = "c")
J2 <- E/(1-1/S)
ggJ2 <- ggplot(data.frame(S, J2), aes(S, J2)) +
  geom_point() + labs(tag = "d")
grid.arrange(ggH, ggJ, ggE , ggJ2, ncol = 2, nrow = 2)

La corrélation entre richesse et équitabilité est donc positive si la richesse varie entre communautés, mais négative si ce n’est qu’un effet de l’échantillonnage. Les résultats sont similaires avec des communautés en log-séries : la corrélation est positive quand \(\alpha\) varie, négative quand l’échantillonnage varie.