12 Décomposition de l’entropie HCDT

L’entropie HCDT \(\gamma\) peut être décomposée en somme de l’entropie \(\alpha\) et la moyenne de la divergence entre la distribution de chaque communauté et celle de la méta-communauté. L’entropie \(\beta\) est donc interprétable comme le gain d’information apporté par la connaissance de la distribution détaillée des communautés en plus de celle, aggrégée, de la méta-communauté. L’entropie \(\beta\) va de pair avec le nombre effectif de communautés, c’est-à-dire le nombre de communautés de même poids, sans aucune espèce commune, qui fourniraient la même valeur d’entropie \(\beta\) que les communautés réelles. La diversité \(\gamma\) se décompose donc en produit du nombre effectif d’espèces de la diversité \(\alpha\) et du nombre effectif de communautés.

Ce chapitre traite de la diversité proportionnelle, qui mesure à quel point les communautés diffèrent de leur assemblage. Dans la littérature, la diversité \(\beta\) est généralement une mesure dérivée (Ellison 2010), c’est-à-dire calculée à partir des diversités \(\alpha\) et \(\gamma\), d’où un abondant débat sur l’indépendance souhaitée mais pas toujours observée entre les valeurs de diversité \(\alpha\) et \(\beta\) (Baselga 2010a; Jost 2010a; Veech et Crist 2010). Un forum a été consacré à la question dans la revue Ecology, conclu par Chao, Chiu, et Hsieh (2012), et une revue a été faite par Tuomisto (2010a, 2010b).

La décomposition de l’entropie HCDT constitue un cadre cohérent dans lequel la diversité \(\beta\) est non seulement une mesure dérivée, mais également une mesure de la divergence entre les distributions des communautés et celle de la méta-communauté.

12.1 Décomposition de l’indice de Shannon

Table 12.1: Table 12.2: Définition explicite de la diversité de Shannon en tant que divergence entre une distribution observée et une distribution attendue. Les indices \(H_\alpha\) et \(H_\gamma\) sont les compléments au logarithme du nombre d’espèces de cette divergence.

Indice	Distribution observée	Distribution attendue	Formule
\(H_\alpha\)	Fréquence des espèces dans la communauté	Fréquences égales, hors formule	\(_{i}H_\alpha = \sum_s{p_{s|i}\ln{p_{s|i}}}\). \(H_\alpha = \sum_i{w_i\,_{i}H_\alpha}\)
\(H_\beta\)	Fréquence des espèces dans la communauté	Fréquence totale des espèces	\(_{i}H_\beta = \sum_s{p_{s|i}\ln{p_{s|i}/p_{s}}}\). \(H_\beta = \sum_i{w_i\,_{i}{H}_\beta}\)
\(H_\gamma\)	Fréquence des espèces dans la méta-communauté	Fréquences égales, hors formule	\(H_\gamma = \sum_s{p_{s}\ln{p_{s}}}\)

12.1.1 Définition

La décomposition explicite (tableau 12.1) est due à Marcon et al. (2012) mais avait été établie plus ou moins clairement plusieurs fois dans la littérature, notamment par Rao et Nayak (1985) : la diversité \(\beta\) est la divergence de Kullback-Leibler entre la distribution des espèces dans chaque parcelle et la distribution moyenne, appelée divergence de Jensen-Shannon (Lin 1991). Les diversités \(\alpha\) et \(\gamma\) sont les compléments à \(\ln{S}\) des indices de dissimilarité de Theil (4.1), divergences de Kullback-Leibler entre les distributions des espèces et leur équiprobabilité.

Lewontin (1972), dans son célèbre article sur la diversité génétique humaine, définit la diversité de Shannon inter-groupe comme la différence entre la diversité totale et la diversité moyenne intra-groupe, mais ne cherche pas à explorer ses propriétés.

La forme de \(H_{\beta}\) a été établie par Ricotta et Avena (2003a), sans la relier à celle de \(H_{\alpha}\) et \(H_{\gamma}\). Enfin, l’idée de la décomposition de la divergence de Kullback-Leibler, mais avec une approche différente, sans rapprochement avec l’indice de Shannon, a été publiée par Ludovisi et Taticchi (2006).

Les méta-communautés peuvent à leur tour être regroupées à un niveau supérieur, la diversité \(\gamma\) du niveau inférieur devenant diversité \(\alpha\) pour le niveau supérieur. La décomposition ou le regroupement peuvent être effectués sur un nombre quelconque de niveaux.

Calcul sous R : La fonction BetaEntropy calcule l’entropie \(\beta\) de la méta-communauté (l’argument \(q=1\) permet de choisir l’entropie de Shannon).

# Pas de correction du biais d'estimation
summary(BetaEntropy(Paracou618.MC, q = 1, Correction = "None"))

## Neutral beta entropy of order 1 of metaCommunity 
## Paracou618.MC with correction: None 
## 
## Entropy of communities: 
##      P006      P018 
## 0.3499358 0.5771645 
## Average entropy of the communities: 
## [1] 0.4471751

12.1.2 Biais d’estimation

L’estimateur du taux de couverture de la communauté \(i\) est noté \(\hat{C}_i\), le taux de couverture total \(\hat{C}\). L’estimateur corrigé de \(_iH_{\beta}\) est

\[\begin{equation} \tag{12.1} _{i}\tilde{H}_{\beta} = \sum^{s_{\ne 0}}_{i=1}{\frac{{\hat{C}}_i{\hat{p}}_{s|i} \ln\frac{{\hat{C}}_i{\hat{p}}_{s|i}}{\hat{C}{\hat{p}}_s}}{1-{\left(1-{\hat{C}}_i{\hat{p}}_{s|i}\right)}^n}}. \end{equation}\]

Calcul sous R : BetaEntropy applique cette correction :

summary(BetaEntropy(Paracou618.MC, q = 1, Correction = "ChaoShen"))

## Neutral beta entropy of order 1 of metaCommunity 
## Paracou618.MC with correction: ChaoShen 
## 
## Entropy of communities: 
##      P006      P018 
## 0.2949188 0.4514132 
## Average entropy of the communities: 
## [1] 0.3618884

Chao, Wang, et Jost (2013) utilisent une approche différente pour corriger le biais d’estimation : l’information mutuelle. Les données sont organisées comme dans le tableau 10.1, mais les probabilités qu’un individu appartienne à la communauté \(i\) et à l’espèce \(s\) sont calculées pour que leur somme soit égale à 1 sur l’ensemble du tableau : \(\sum_s{\sum_i{p_{s,i}}}=1\) (au lieu de \(\sum_i{p_{s|i}}=1\)).

L’information mutuelle est la divergence de Kullback-Leibler entre la distribution de \(\{p_{s,i}\}\) et celle du produit des distributions marginales \(\{p_s\}\) et \(\{p_i\}\). Si les distributions marginales sont indépendantes, la probabilité \(p_{s,i}\) qu’un individu appartienne à l’espèce \(s\) et se trouve dans la communauté \(i\) est donnée par le produit des probabilités marginales \(p_s\) et \(p_i\), et l’information mutuelle est nulle.

L’information mutuelle se calcule comme la différence entre l’entropie de Shannon calculée sur l’ensemble du tableau \(H(\{p_{s,i}\})\) et les entropies marginales \(H(\{p_s\})\) et \(H(\{p_i\})\). \(H(\{p_s\})\) est l’entropie \(\gamma\) de la méta-communauté. Si on choisit de pondérer les communautés par leurs effectifs (\(w_i=p_i\)), alors \(H(\{p_{s,i}\})-H(\{p_i\})\) est l’entropie \(\alpha\) de la méta-communauté, c’est-à-dire la moyenne pondérée des entropies \(\alpha\) des communautés. Dans ce cas, l’entropie \(\beta\) est égale à l’opposée de l’information mutuelle. Comme chaque terme du calcul est une entropie \(\alpha\), il peut être corrigé selon l’équation (3.41) pour obtenir un estimateur moins biaisé de \(H_{\beta}\).

Calcul sous R :

Shannon(Paracou618.MC$Ns) + Shannon(colSums(Paracou618.MC$Nsi)) -
    Shannon(Paracou618.MC$Nsi)

##   UnveilJ 
## 0.3439827

Cet estimateur est le moins biaisé à ce jour, mais n’est applicable qu’à l’entropie de Shannon, sous la condition que la pondération des communautés soit donnée par les effectifs.

Z. Zhang et Grabchak (2014) proposent un estimateur de la divergence de Kullback-Leibler avec un biais réduit selon la même méthode que pour l’estimation de l’entropie HCDT ou de l’entropie de Shannon :

\[\begin{align} \tag{12.2} _{i}\tilde{H}_{\beta} &= \sum^{s_{\ne 0}}_{s=1}{\frac{n_{s,i}}{n} }\\ &\left\{ \sum^{n-n_s}_{v=1}{\frac{1}{v} \prod^v_{j=1}{ \left( 1-\frac{n_s}{n-j+1} \right) }} - \sum^{n_i-n_{s,i}}_{v=1}{\frac{1}{v} \prod^v_{j=1}{\left( 1-\frac{n_{s,i}-1}{n_i-j} \right) }} \right\}. \end{align}\]

Cette correction est incluse dans la fonction ShannonBeta de entropart :

# Divergence de Kullback-Leibler entre chaque communauté de
# Paracou618.MC et la métacommunauté
(Beta <- apply(Paracou618.MC$Nsi, 2, ShannonBeta, Nexp = Paracou618.MC$Ns,
    Correction = "ZhangGrabchak"))

##      P006      P018 
## 0.1442318 0.2994995

# Entropie beta
sum(Paracou618.MC$Wi * Beta)

## [1] 0.2106764

La correction de Zhang et Grabchak réduit beaucoup plus fortement l’estimation que celle de Chao et Shen. Le meilleur estimateur peut être évalué à partir de la différence entre les entropies \(\gamma\) et \(\alpha\), corrigées par le meilleur estimateur disponible (celui de Chao, Wang et Jost, voir section 3.3.2) :

# Entropie alpha de chaque communauté de Paracou618.MC
(Alpha <- apply(Paracou618.MC$Nsi, 2, Shannon, CheckArguments = FALSE))

##     P006     P018 
## 4.427559 4.772981

# Entropie beta estimée par différence
bcShannon(Paracou618.MC$Ns) - sum(Paracou618.MC$Wi * Alpha)

##   UnveilJ 
## 0.3526572

L’estimateur de Chao et Shen est apparemment le meilleur, la correction de celui de Zhang et Grabchak est trop forte.

12.2 Décomposition de l’entropie généralisée

La décomposition additive de l’entropie selon Lande (1996) doit être la suivante :

\[\begin{equation} \tag{12.3} ^{q}\!H_{\gamma} = {^{q}\!H_{\alpha}} + {^{q}\!H_{\beta}}. \end{equation}\]

Bourguignon (1979) comme Lande (1996) définissent une mesure d’inégalité décomposable comme respectant les propriétés suivantes :

• La population totale étant partitionnée, chaque partition recevant un poids \(w_i\), la composante intra-groupe de la mesure \(H_{\alpha}\) est égale à la somme pondérée des mesures dans chaque-groupe \(H_{\alpha}=\sum_i{w_i {_{i}\!H_{\alpha}}}\) ;
• La composante intergroupe \(H_{\beta}\) est la mesure d’inégalité entre les groupes ;
• La mesure totale \(H_{\gamma}\) est la somme des mesures intra et intergroupes.

En passant par les nombres de Hill, Jost (2007) montre que l’indice de Shannon est le seul pouvant être décomposé de cette façon.

La démonstration de Jost repose sur le postulat que la transformation de l’entropie en nombre de Hill, définie pour la diversité \(\alpha\), doit avoir la même forme pour la diversité \(\beta\). La remise en cause de ce postulat (Marcon et al. 2014) permet de décomposer la diversité d’ordre quelconque quel que soit le poids des communautés.

La décomposition de l’entropie est faite en écrivant le logarithme d’ordre \(q\) de la décomposition de la diversité, équation (10.1) :

\[\begin{equation} \tag{12.4} ^{q}\!H_{\gamma} = {^{q}\!H_{\alpha}}+\ln_q{^{q}\!D_{\beta}}-\left(q-1\right){^{q}\!H_{\alpha}}\ln_q{^{q}\!D_{\beta}}. \end{equation}\]

Ceci est la décomposition de Jost (2007). Jost désigne sous le nom de “composante \(\beta\) de l’entropie” le logarithme d’ordre \(q\) de la diversité, qu’il note \(H_B\). La décomposition n’est pas additive, mais \(H_B\) est indépendant de l’entropie \(\alpha\).

Les deux derniers termes peuvent être regroupés et réarrangés pour obtenir \(^{q}\!H_{\beta}\) conformément à la décomposition additive de l’équation (12.3) :

\[\begin{equation} \tag{12.5} ^{q}\!H_{\beta} = \sum_i{w_i\sum_s{p^q_{s|i}\ln_q\frac{p_{s|i}}{p_s}}}. \end{equation}\]

L’entropie \(\beta\) est la somme pondérée par \(w_i\) (et pas autrement) des contributions de chaque communauté :

\[\begin{equation} \tag{12.6} ^{q}_{i}\!H_{\beta}=\sum_s{p^q_{s|i}\ln_q\frac{p_{s|i}}{p_s}}. \end{equation}\]

\(^{q}_{i}\!H_{\beta}\) est une divergence de Kullback-Leibler généralisée (Borland, Plastino, et Tsallis 1998; Tsallis, Mendes, et Plastino 1998). \(^{q}\!H_{\beta}\) en est la moyenne sur l’ensemble des communautés, c’est donc une généralisation de la divergence de Jensen-Shannon (Marcon et al. 2014). \(^{q}\!H_{\gamma}\) peut s’écrire sous la forme \(^{q}\!H_{\gamma} = -\sum_s{p^q_s}\ln_q{p_s}\) : la formalisation de la décomposition est une généralisation de la décomposition de l’entropie de Shannon, résumée dans le tableau 12.3.

Il est intéressant d’écrire \(^{q}_{i}\!H_{\beta}\) et \(^{q}\!H_{\gamma}\) sous la forme d’entropies, pour faire apparaître leur fonction d’information. Pour \(q\) différent de 1, l’entropie \(\gamma\) est

\[\begin{equation} \tag{12.7} ^{q}\!H_{\gamma} = \sum_s{p_s\frac{1-p^{q-1}_s}{q-1}} = \sum_s{p_s\ln_q\frac{1}{p_s}}. \end{equation}\]

Sa fonction d’information a été tracée figure 4.1.

L’entropie \(\beta\) est

\[\begin{equation} \tag{12.8} ^{q}_{i}\!H_{\beta} = \sum_s{p_{s|i}\frac{p^{q-1}_{s|i}-p^{q-1}_s}{q-1}} = \sum_s{p_{s|i}\left(\ln_q\frac{1}{p_s}-\ln_q\frac{1}{p_{s|i}}\right)}. \end{equation}\]

La forme de l’entropie \(\beta\) évoque la divergence de puissance (N. Cressie et Read 1984) qui est une statistique qui mesure la divergence entre deux distributions dont les propriétés asymptotiques sont connues. La divergence de puissance peut être écrite sous la forme \(I_q= \frac{-2}{q} \sum_s{p_{s|i} \ln_q\frac{p_{s}}{p_{s|i}}}\). Elle est égale à (deux fois) la divergence de Kullback-Leibler pour \(q=1\), mais diffère de l’entropie \(\beta\) pour les autres valeurs de \(q\). La divergence non-logarithmique de Jensen-Shannon (Lamberti et Majtey 2003) est identique à une normalisation près : \(K_q= -\sum_s{p_{s|i} \ln_q\frac{p_{s}}{p_{s|i}}}\). Elle mesure l’écart entre la diversité \(\alpha\) et la valeur de \(\sum_s{w_i p^q_{s|i} \ln_q{p_s}^q}\), qui n’est pas la diversité \(\gamma\) (Marcon et al. 2014).

Calcul sous R : La fonction DivPart calcule entropie et diversité en même temps :

DivPart(q = 1, Paracou618.MC, Biased = FALSE)

## $MetaCommunity
## [1] "Paracou618.MC"
## 
## $Order
## [1] 1
## 
## $Biased
## [1] FALSE
## 
## $Correction
## [1] "UnveilJ"
## 
## $Normalized
## [1] TRUE
## 
## $TotalAlphaDiversity
## [1] 97.06467
## 
## $TotalBetaDiversity
##  UnveilJ 
## 1.422843 
## 
## $GammaDiversity
##  UnveilJ 
## 138.1078 
## 
## $CommunityAlphaDiversities
##     P006     P018 
##  83.7268 118.2713 
## 
## $TotalAlphaEntropy
## [1] 4.575378
## 
## $TotalBetaEntropy
##   UnveilJ 
## 0.3526572 
## 
## $GammaEntropy
##  UnveilJ 
## 4.928035 
## 
## $CommunityAlphaEntropies
##     P006     P018 
## 4.427559 4.772981 
## 
## $CommunityBetaEntropies
## [1] NA
## 
## $Method
## [1] "HCDT"
## 
## attr(,"class")
## [1] "DivPart"

12.3 Décomposition du nombre d’espèces

Les résultats généraux se simplifient pour \(q=0\). L’entropie \(\gamma\) est le nombre d’espèces de la méta-communauté moins un (\(^{0}\!H_{\gamma}=S-1\)), l’entropie \(\alpha\) est la moyenne pondérée du nombre d’espèces des communautés moins un (\(^{0}\!H_{\alpha}=\bar{S}-1\)), l’entropie \(\beta\) est la différence : \(^{0}\!H_{\beta}=S-\bar{S}\).

En termes de diversité,

\[\begin{equation} \tag{12.9} ^{0}\!D_{\beta}=\frac{S}{\bar{S}}. \end{equation}\]

\(^{0}\!D_{\beta}\) peut être supérieur au nombre de communautés (Chao, Chiu, et Hsieh 2012) si les poids sont très inégaux, ce qui complique son interprétation. La pondération de Jost donne pour le nombre d’espèces le même poids à toutes les communautés et garantit \(^{0}\!D_{\beta}\le I\), ce qui constitue pour Chao et al. un argument en faveur de son utilisation. Un contre-argumentaire est fourni par Marcon et al. (2014). Quel que soit la distribution des poids des communautés, il est toujours possible de ramener les données à un ensemble de communautés de poids identiques, dont certaines sont répétées. La communauté dont le poids \(w_{min}\) est le plus faible est représentée une seule fois, les autres \({w_i}/{w_{min}}\) fois. L’indépendance entre les diversités \(\alpha\) et \(\beta\) est donc bien vérifiée. Le diversité \(\beta\) maximale théorique est \({1}/{w_{min}}\) (et non \(I\)). Elle n’est pas atteinte parce que plusieurs communautés sont identiques.

La définition de la diversité \(\beta\) par Whittaker (1960) s’appliquait aux données de présence-absence. La diversité \(\beta\) était le rapport entre le nombre d’espèces total de l’assemblage des communautés (diversité \(\gamma\)) et le nombre moyen d’espèces dans chaque communauté (diversité \(\alpha\)). C’est précisément la définition de \(^{0}\!D_{\beta}\) (12.9).

12.4 Décomposition de l’indice de Gini-Simpson

L’entropie de Simpson peut aussi être décomposée comme une variance. La probabilité qu’un individu appartienne à l’espèce \(s\) est \(p_s\). Elle suit une loi de Bernoulli, dont la variance est \(p_s\left(1-p_s\right)\). Cette variance peut être décomposée entre les communautés, où la probabilité est \(p_{s|i}\). La décomposition entre variance intra et inter-communautés est

\[\begin{equation} \tag{12.10} p_s\left(1-p_s\right)=\sum_i{w_i\left[p_{s|i}\left(1-p_{s|i}\right)+{\left(p_{s|i}-p_s\right)}^2\right]}. \end{equation}\]

Cette égalité peut être sommée sur toutes les espèces pour donner

\[\begin{equation} \tag{12.11} E_{\gamma}=\sum_i{w_i E_{\alpha,i}}+\sum_i{w_i\sum_s{{\left(p_{s|i}-p_s\right)}^2}}=E_{\alpha}+E_{\beta}. \end{equation}\]

L’entropie \(\gamma\) de Simpson peut être décomposée en sa diversité \(\alpha\), somme pondérée des entropies \(\alpha\) des communautés, et son entropie \(\beta\), égale à la somme pondérée des distances \(l^2\) entre la distribution des fréquences dans chaque communauté et celle de l’ensemble de la communauté.

En génétique, l’égalité s’écrit(Nei 1973) \(H_t=H_s+D_{s,t}\). \(H_t\) est l’hétérozygotie totale, décomposée en \(H_s\), l’hétérozygotie moyenne des populations et \(D_{s,t}\) la différenciation absolue entre populations. \(G_{s,t}={D_{s,t}}/{H_t}\) est la différenciation relative.

L’entropie \(E_{\beta}\) calculée de cette manière est égale à \(^{2}\!H_{\beta}\) calculée à l’équation (12.8) pour le cas général, mais la contribution de chaque communauté est différente : la décomposition de la variance est une façon alternative de décomposer l’entropie, valable uniquement pour l’entropie de Simpson.

Cette décomposition est remise en cause par Jost (Jost 2007, 2008) qui a généré le débat (Heller et Siegismund 2009; Ryman et Leimar 2009; Jost 2009a; Whitlock 2011). \(E_{\gamma}\) étant inférieure ou égale à 1, \(E_{\beta}\) n’est pas indépendante de \(E_{\alpha}\) : seule la décomposition multiplicative permet l’indépendance, et Jost propose d’utiliser une transformation de \(^{2}\!D_{\beta}\) comme mesure de différenciation (voir section 12.7.2). Gregorius (2014) montre que ce problème n’est pas limité à l’entropie de Simpson mais s’applique à toutes les entropies HCDT d’ordre supérieur à 1.

Jost postule que la diversité \(\beta\) de Simpson a la même relation à \(E_{\beta}\) que les diversités \(\alpha\) et \(\gamma\),

\[\begin{equation} \tag{12.12} ^{q}\!D_{\gamma} = {^{q}\!D_{\alpha}}{^{q}\!D_{\beta}} \Leftrightarrow \frac{1}{1-E_{\gamma}}=\frac{1}{1-E_{\alpha}}\frac{1}{1-E_{\beta}}, \end{equation}\]

d’où une décomposition additive différente, qui correspond à sa décomposition générale (12.4) :

\[\begin{equation} \tag{12.13} E_{\gamma}=E_{\alpha}+E_{\beta}-{E_{\alpha}}{E_{\beta}}. \end{equation}\]

Il n’y a en réalité aucune raison pour que le nombre équivalent de la diversité \(\beta\) ait la même forme que celle de la diversité \(\alpha\) : les deux diversités sont par nature très différentes, et Hill ne traitait pas la diversité \(\beta\). La diversité de Shannon est exceptionnelle parce que, pour des raisons différentes, son nombre de Hill est l’exponentielle de l’entropie, et l’exponentielle de la décomposition additive (12.3) est la décomposition multiplicative (10.1).

Table 12.3: Table 12.4: Entropie, diversité et décomposition. L’entropie \(\alpha\) de chaque communauté se calcule comme l’entropie \(\gamma\)

Mesure de diversité	Entropie généralisée	Shannon
Entropie \(\gamma\)	\(^{q}\!H_{\gamma}=-\sum_s{p^q_s}\ln_q{p_s}\)	\(^{1}\!H_{\gamma}=-\sum_s{p_s}\ln{p_s}\)
Entropie \(\beta\)	\(^{q}\!H_{\beta}=\sum_i{w_i\sum_s{p_{s|i}\left(\ln_q\frac{1}{p_s}-\ln_q\frac{1}{p_{s|i}}\right)}}\)	\(^{1}\!H_{\beta}=\sum_i{w_i\sum_s{p_{s|i}\ln\frac{p_{s|i}}{p_s}}}\)
Diversité \(\gamma\) (nombre de Hill)	\(^{q}\!D_{\gamma}=e^{^q\!H_{\gamma}}_q\)	\(^{1}\!D_{\gamma}=e^{^1\!H_\gamma}\)
Diversité \(\beta\) (nombre équivalent	\(^{q}\!D_{\beta}=e^{\frac{^{q}\!H_{\beta}}{1-(q-1)^{q}\!H_{\alpha}}}_q\)	\(^{1}\!D_{\beta}=e^{^{1}\!H_{\beta}}\)

Le nombre équivalent de communautés a une forme légèrement différente d’un nombre de Hill (tableau 12.3).

12.5 Décomposition de l’indice de Rao

Les notations sont celles de la présentation de l’indice de Rao, section 7.6.

La diversité de la méta-communauté, peut être décomposée en une somme (pondérée) de diversités intra et une diversité inter (Pavoine, Dufour, et Chessel 2004) en définissant une dissimilarité entre les communautés \(i\) et \(j\) :

\[\begin{equation} \tag{12.14} D_{H_{\Delta }}\left(\mathbf{p}_i,\mathbf{p}_j\right) = 2 H_{\Delta}\left(\frac{\mathbf{p}_{i}+\mathbf{p}_j}{2}\right) -H_{\Delta}\left(\mathbf{p}_i\right)-H_{\Delta}\left(\mathbf{p}_j\right). \end{equation}\]

Elle est définie par Rao comme la différence entre l’entropie quadratique du mélange des deux communautés et celles des deux communautés prises individuellement. Elle peut être utilisée pour calculer un indice de diversité entre communautés, de la même façon qu’on calcule la diversité entre espèces d’une communauté :

\[\begin{equation} \tag{12.15} H_{\Delta }\left(\mathbf{p}\right) = \sum_i{w_i H_{\Delta }\left({\mathbf{p}}_i\right)}+\sum_i{\sum_j{w_i w_j D_{H_{\Delta }}\left({\mathbf{p}}_i,{\mathbf{p}}_j\right)}}. \end{equation}\]

Le deuxième terme de la somme est la diversité inter-communautés. C’est un indice de Rao : les poids des communautés sont équivalents aux tableaux de fréquences et les dissimilarités entre communautés sont équivalentes aux dissimilarités entre espèces de l’équation (7.20). La divergence entre communautés est construite à partir des entropies de chacune : l’entropie \(\beta\) est définie comme la différence entre les entropies \(\gamma\) et \(\alpha\).

L’exemple suivant utilise les communautés du fichier rao.effectifs.csv :

# Vecteur contenant 8 espèces...
(read.csv2("data/rao.effectifs.csv", row.names = 1, header = T) ->
    effectifs)

##     P1 P2 P3 P4
## Ess 97 36 34 61
## Me  62 24 49  4
## S1   4  6  6 75
## Sr  71 78 99 36
## Vm  76 29 34  2
## Bg  58 49 47 19
## Ef   9 34 91 35
## Dg  98 14 95 14

# Lecture des données : traits pour 34 espèces
read.csv2("data/rao.traits.csv", row.names = 1, header = T) ->
    traits
# ACP sur les traits foliaires
pcaf <- dudi.pca(traits, scale = T, scannf = FALSE, nf = 2)
# CAH Ward des traits foliaires
hf <- hclust(dist(pcaf$tab), "ward.D")
# Transformation de l'arbre du format hclust au format
# phylog
phyf <- hclust2phylog(hf)

Il contient 4 communautés.

Pour obtenir tous les éléments de l’équation (12.15) :

• \(H_{\Delta }\left(\mathbf{p}\right)\) : diversité totale. Calculer \(\mathbf{p}\) en sommant les communautés. Calculer ensuite l’entropie quadratique avec divc :

(tabF <- apply(effectifs[names(phyf$leaves), ], MARGIN = 1, sum))

##  Sr Ess  Me  S1  Bg  Ef  Vm  Dg 
## 284 228 139  91 173 169 141 221

divc(as.data.frame(tabF), phyf$Wdist)

##      diversity
## tabF  5.870667

• \(H_{\Delta}\left({\mathbf{p}}_i\right)\) : diversité de chaque communauté, fournie par divc :

divc(effectifs[names(phyf$leaves), ], phyf$Wdist)

##    diversity
## P1  5.816719
## P2  5.897210
## P3  5.744483
## P4  4.790586

• La variabilité inter-communautés peut être calculée par divc en utilisant la distance fournie par disc, en définissant la matrice des poids (égale aux effectifs) :

divc(as.data.frame(colSums(effectifs)), disc(effectifs[names(phyf$leaves),
    ], phyf$Wdist))

##                    diversity
## colSums(effectifs) 0.2362187

La fonction disc calcule \(\sqrt{2D_{H_{\Delta}}\left({\mathbf{p}}_i,{\mathbf{p}}_j\right)}\) :

disc(effectifs[names(phyf$leaves), ], phyf$Wdist)

##           P1        P2        P3
## P2 0.4698121                    
## P3 0.4888729 0.6487916          
## P4 1.0018983 0.8776582 1.3157902

Une interprétation géométrique de la décomposition est la suivante (Pavoine, Dufour, et Chessel 2004). Les espèces peuvent être placées dans un espace multidimensionnel construit par une Analyse en Coordonnées Principales (Gower 1966) de la matrice de dissimilarité \(\mathbf{D}\) telle que \(\mathbf{\Delta}={\mathbf{D}^{\circ2}}/{2}\) (les distances dans l’espace multidimensionnel sont \(\sqrt{2\delta_{s's''}}\) ; autrement dit : la dissimilarité entre deux espèces est la moitié du carré de la distance entre elles dans la représentation géométrique). Chaque communauté se trouve au centre de gravité des espèces qu’elle contient, pondérées par leur fréquence. La moitié du carré de la distance entre deux communautés dans ce même espace est le coefficient de dissimilarité entre communautés de Rao. La distance entre communautés est donc interprétable directement comme une mesure de diversité \(\beta\) (Ricotta et al. 2015), dans la tradition de l’utilisation de la dissimilarité entre paires de communautés (chapitre 11).

Cette partition suppose que les poids des communautés sont proportionnels à leur nombre d’individus (Rao 1982; Villéger et Mouillot 2008). O. J. Hardy et Senterre (2007) décomposent (par différence entre \(\gamma\) et \(\alpha\)) l’indice de Rao de communautés de poids égaux. O. J. Hardy et Jost (2008) montrent que les deux pondérations sont valides mais l’absence de cadre général assurant que la diversité \(\gamma\) de Rao est supérieure à la diversité \(\alpha\) (de Bello et al. 2010) motive Guiasu et Guiasu (2011) à proposer une alternative à l’indice de Rao, l’indice de Gini-Simpson quadratique pondéré (7.24), dont la concavité est démontrée (ce qui implique que \(\gamma\ge \alpha\)). La pondération peut en fait être quelconque tant que la matrice dont les éléments sont la racine carré des éléments de la matrice de dissimilarité est euclidienne (Champely et Chessel 2002). Ce résultat a été obtenu pour les arbres ultramétriques dans le cadre plus général de la décomposition de l’entropie phylogénétique (voir chapitre 12.

La partition peut être faite avec la fonction DivPart :

# Création d'une méta-communauté, poids égaux aux effectifs
MC <- MetaCommunity(effectifs, colSums(effectifs))
summary(DivPart(q = 2, MC, Tree = phyf, Normalize = FALSE))

## HCDT diversity partitioning of order 2 of metaCommunity MC
## 
## Phylogenetic or functional diversity was calculated
## according to the tree 
## phyf 
## 
## Diversity is not normalized 
## 
## Alpha diversity of communities: 
##       P1       P2       P3       P4 
## 24.19203 24.70000 23.75363 19.16686 
## Total alpha diversity of the communities: 
##        9 
## 23.11553 
## Beta diversity of the communities: 
##        9 
## 1.061198 
## Gamma diversity of the metacommunity: 
##        9 
## 24.53015

La décomposition de la diversité (et non seulement de l’entropie) de Rao a été établie par Ricotta et Szeidl (2009).

12.6 Synthèse

La diversité mesurée par l’entropie généralisée peut être décomposée dans tous les cas de figure, y compris lorsque les poids des communautés ne sont pas égaux. Les formules d’entropie et de diversité sont résumées dans le tableau 12.3. L’entropie \(\beta\) est une mesure de divergence entre la distribution de chaque communauté et celle de la méta-communauté, comme l’avaient suggéré Ricotta et Burrascano (2009).

L’entropie de Shannon est un cas particulier dans lequel toutes les controverses disparaissent : l’entropie \(\beta\) est indépendante de l’entropie \(\alpha\), et la pondération de Jost se confond avec celle de Routledge.

L’entropie de Simpson peut être décomposée de deux façons : comme une variance quand les poids des communautés sont donnés par leurs effectifs, ou selon le cas général. Les deux décompositions produisent les mêmes valeurs d’entropie \(\beta\), mais la contribution de chaque communauté n’est pas la même.

L’entropie peut être décomposée hiérarchiquement sur plusieurs niveaux (Crist et al. 2003; Marcon et al. 2012).

Les probabilités d’occurrence des espèces ne sont pas connues mais estimées à partir des données. Les diversités \(\alpha\) et \(\gamma\) sont sous-estimées et la diversité \(\beta\) surestimée (Marcon et al. 2012; J. Beck, Holloway, et Schwanghart 2013), d’autant plus que l’ordre de diversité est faible (le biais est négligeable au-delà de l’indice de Simpson). Des méthodes de correction existent, mais pas pour l’entropie \(\beta\) à l’exception de Shannon. La méthode générale consiste donc à corriger les entropies \(\alpha\) et \(\gamma\), calculer l’entropie \(\beta\) par différence et transformer les résultats en nombres équivalents (Marcon et al. 2014; Marcon, Zhang, et Hérault 2014).

12.7 Normalisation

La mesure de diversité \(^{q}\!D_{\beta}\) est le nombre équivalent de communautés totalement distinctes qui fourniraient ce niveau de diversité.

12.7.1 Nécessité de normaliser la diversité \(\beta\)

Selon une première approche, cette mesure n’a de sens que comparée à nombre de communautés. La diversité entre un hectare de forêt tropicale et un hectare de forêt tempérée (de même poids, sans espèce commune) est égale à 2 quel que soit \(q\). La diversité entre un nombre suffisant d’échantillons de forêt tropicale relativement homogène (avec de nombreuses espèces communes) peut facilement dépasser 2 : c’est le cas des 50 carrés de BCI pour \(q=0\). Pour ne pas conclure de façon erronée que les carrés de BCI sont plus différents entre eux que BCI et la forêt de Fontainebleau, Jost (2007) suggère de diviser la diversité \(\beta\) par le nombre de communautés pour la normaliser. Ce raisonnement a un sens quand la diversité maximale envisageable est effectivement égale au nombre de communautés, par exemple si les communautés sont choisies dans des habitats différents : la diversité \(\beta\) mesure cette différence.

Un autre cas est envisageable : les communautés peuvent être des échantillons d’une méta-communauté clairement définie. La diversité \(\beta\) mesure alors la variabilité de l’échantillonnage à l’intérieur de la méta-communauté à une échelle donnée. Pour une taille d’échantillon fixée (par exemple un hectare de forêt), la diversité \(\beta\) ne dépend pas du nombre de communautés : l’entropie \(\beta\) est l’espérance (estimée par la moyenne, équation (12.5) de la divergence de Jensen-Shannon entre la distribution des espèces d’une communauté et celle de la méta-communauté, fixe. Cette variabilité dépend de l’échelle de l’échantillonnage dans le sens où elle diminue si les échantillons sont de taille plus grande : l’entropie \(\alpha\) de deux hectares de forêts est la diversité \(\alpha\) moyenne de chacun des deux hectares plus l’entropie \(\beta\) entre eux. L’entropie \(\beta\) entre les échantillons de deux hectares est donc diminuée de cette entropie \(\beta\) “intra” qui est absorbée par la nouvelle entropie \(\alpha\) quand la taille des échantillons augmente.

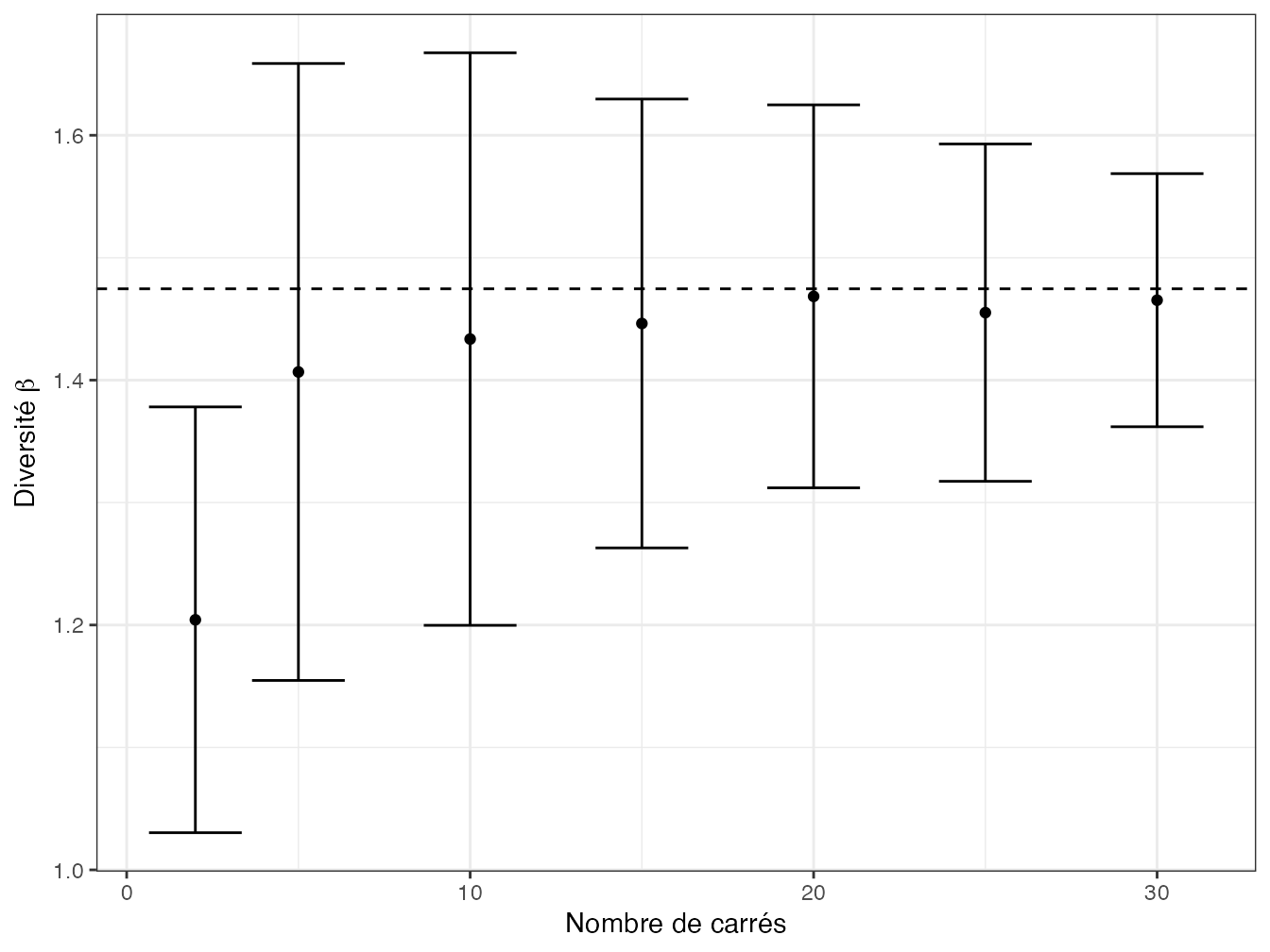
Figure 12.1: Estimation de la diversité \(\beta\) entre carrés de BCI. La diversité est calculée à partir du nombre de carrés en abscisse, de 2 à 30, tirés aléatoirement. La valeur en ordonnée est la diversité d’ordre 2 moyenne sur 100 tirages, les barres représentent l’écart-type. Aux erreurs d’estimation près et dès 5 carrés (nécessaires pour représenter l’ensemble du dispositif), la valeur de la diversité \(\beta\) ne dépend pas du nombre de carrés. La ligne horizontale représente la diversité \(\beta\) entre tous les carrés.

La figure 12.1 présente les valeurs estimées de diversité neutre \(\beta\) entre carrés de BCI tirés aléatoirement, en fonction du nombre de carrés.

Code pour réaliser la figure :

# Metacommunauté de BCI
MC <- MetaCommunity(as.data.frame(t(BCI)))

# Création d'une méta-communauté à partir de n carrés de BCI 
SamplePlots <- function (n, q) {
  Plots <- sample(1:50, n)
  Nsi <- MC$Nsi[, Plots]; MCsample <- MetaCommunity(Nsi)
  dp <- DivPart(q, MCsample, Biased = FALSE)
  # Retourne la diversité beta
  return(dp$TotalBetaDiversity)
}
# Calcul de la diversité moyenne à partir des simulations
BetaPlots <- function (q, nPlots, nSimulations) {
  buiw <- b <- vector("numeric", length(nPlots)); i <- 1
  for (Size in nPlots) {
    Sims <- replicate(nSimulations, SamplePlots(Size, q))  
    b[i] <- mean(Sims)
    buiw[i] <- sd(Sims)
    i <- i+1
  }
  # Retour d'un dataframe
  return(data.frame(x=nPlots, y=b, ymin=b-buiw, ymax=b+buiw))
}

# Echantillonnage de la diversité beta
BetaD <- BetaPlots(q = 2, nPlots=c(2, 5, 10, 15, 20, 25, 30), 
          nSimulations = 100)
# Diversité beta totale
dpBCI <- DivPart(q = 2, MC, Biased = FALSE)
# Figure
ggplot(BetaD) +
  geom_point(aes(x=x, y=y)) + 
  geom_errorbar(aes(x=x, ymin=ymin, ymax=ymax)) +
  geom_hline(yintercept = dpBCI$TotalBetaDiversity, lty=2) +
  labs(x="Nombre de carrés", 
       y=expression(paste("Diversité ", beta)))

L’estimation de la diversité présente les difficultés classiques dues au biais d’estimation : la diversité \(\gamma\) est sous-estimée si l’échantillonnage est trop faible, la diversité \(\beta\) augmente avec le nombre de communautés comme la diversité \(\gamma\) augmente avec la taille de l’échantillon ; il s’agit d’un problème d’estimation, pas de normalisation.

La diversité \(\beta\) ne doit donc pas être normalisée systématiquement, mais seulement dans le premier cas.

12.7.2 L’indice de chevauchement \(C_{qN}\)

Plutôt qu’une simple normalisation, Chao et al. (2008) définissent un indice de chevauchement, c’est-à-dire la proportion d’espèces partagées en moyenne par une communauté. Si \(N\) communautés (le nombre de communautés est noté \(N\) ici et non \(I\) pour conserver le nom de l’indice établi dans la littérature) de mêmes diversités \(\alpha\) et \(\gamma\) que les données, contenaient chacune \(S\) espèces équifréquentes, dont \(A\) seraient communes à toutes les communautés et les autres représentées dans une seule, \(A/S\) serait cet indice de chevauchement.

Pour \(q\ne 1\),

\[\begin{equation} \tag{12.16} C_{qN} = {\left[{\left(\frac{1}{^{q}\!D_{\beta}}\right)}^{q-1}-{\left(\frac{1}{N}\right)}^{q-1}\right]}/{\left[1-{\left(\frac{1}{N}\right)}^{q-1}\right]} \end{equation}\]

et

\[\begin{equation} \tag{12.17} C_{1N} =\frac{1}{\ln{N}}\sum^S_{s=1}{\sum^N_{i=1}{\frac{p_{s|i}}{N}\ln\left(1+\frac{\sum_{j\ne i}{p_{sj}}}{p_{s|i}}\right)}} =1-\frac{H_{\beta}}{\ln{N}}. \end{equation}\]

\(C_{qN}\) a été défini à l’origine pour \(q\ge 2\). Chao, Chiu, et Hsieh (2012) l’étendent sans précaution à \(q\) quelconque. Sa valeur peut être négative pour \(q<1\), on se limitera donc à \(q \ge 1\).