11 Diversité de différentiation

La diversité \(\beta\) de différentiation mesure la dissimilarité entre communautés, généralement considérées par paires. Les dissimilarités les plus connues sont celles de Jaccard ou de Sørensen. Ces mesures peuvent prendre en compte la seule présence ou absence des espèces, leur abondance ou même la similarité entre les espèces, peuvent être traitées par l’analyse multivariée et être testées contre l’hypothèse de nullité de la dissimilarité.

La littérature des indices de similarité est bien antérieure à celle de la biodiversité. De nombreuses mesures de dissimilarité entre paires de communautés existent donc, et leurs propriétés ont été bien étudiées. Elles seront présentées ici en fonction des types de données qu’elles traitent : présence-absence, abondance ou abondance et similarité des espèces. Enfin, des tests statistiques ont été construits pour rejeter l’hypothèse que les communautés sont issues d’une même méta-communauté par un simple tirage multinomial des espèces.

Une limite importante des mesures de dissimilarité est qu’elles sont très sensibles à la taille des communautés échantillonnées (Wolda 1981).

11.1 Données de présence-absence

11.1.1 Indices de similarité

Les indices les plus simples et probablement les plus connus pour calculer la diversité \(\beta\) sont l’indice de Jaccard (1901) et de Sørensen (Czekanowski 1913; Dice 1945; Sørensen 1948). Ils sont définis pour deux communautés et comptent la proportion d’espèces qu’elles partagent. Plus elle est faible, moins la composition spécifique des communautés est semblable, plus la diversité \(\beta\) est considérée comme grande.

Précisément, notons \(s_{1,1}\) les espèces observées dans les deux communautés, \(s_{1,0}\) celles observées dans la première communauté mais pas la deuxième (et de même \(s_{0,1}\)). L’indice de Jaccard est le rapport entre le nombre d’espèces communes et le nombre d’espèces total :

\[\begin{equation} \tag{11.1} S_3 = \frac{s_{1,1}}{s_{1,1}+s_{1,0}+s_{0,1}}. \end{equation}\]

L’indice de Sørensen vaut deux fois le nombre d’espèces communes divisé par la somme du nombre d’espèces des deux communautés :

\[\begin{equation} \tag{11.2} S_7 = \frac{2s_{1,1}}{2s_{1,1}+s_{1,0}+s_{0,1}}. \end{equation}\]

Les notations \(S_n\) correspondent à celles de l’article de référence de Gower et Legendre (1986) qui fait la revue de ces indices de similarité (13 autres sont traités) et en étudie les propriétés. Certains indices prennent en compte les espèces absentes des deux communautés mais qui auraient pu être observées \(s_{0,0}\).

Deux autres indices sont mentionnés ici, celui de Sokal et Sneath (1963) et celui d’Ochiai (1957) :

\[\begin{equation} \tag{11.3} S_5 = \frac{s_{1,1}}{s_{1,1}+2 \left(s_{1,0}+s_{0,1}\right)}; \end{equation}\] \[\begin{equation} \tag{11.4} S_{12} = \frac{s_{1,1}}{\sqrt{\left(s_{1,1}+s_{1,0}\right)\left(s_{1,1}+s_{0,1}\right)}}. \end{equation}\]

Une propriété importante est la possibilité de comparer plusieurs communautés en calculant la matrice de leurs dissimilarités deux à deux et en en faisant une représentation graphique. Pour cela, la similarité est transformée en dissimilarité \(D_n=1-S_n\) (les similarités sont construites pour être comprises entre 0 et 1). \(D_n\) n’est pas toujours une distance euclidienne, mais \(\sqrt{D_n}\) l’est pour la majorité des indices. On utilisera donc généralement la matrice de distances euclidiennes \(\Delta\) dont chaque élément \(d_{i,j}\) est la racine de la dissimilarité \(\sqrt{D_n}\) calculée entre les communautés \(i\) et \(j\).

Exemple : l’indice de Jaccard peut être calculé pour tous les carrés de BCI comparés deux à deux. La fonction dist.binary du package ade4 calcule \(\sqrt{D_n}\) pour 10 indices de similarité étudiés par Gower et Legendre (voir l’aide de la fonction). Le résultat est une demi-matrice de distances de classe dist.

library("vegan")
data(BCI)
library("ade4")
DistJaccard <- dist.binary(BCI, method = 1)

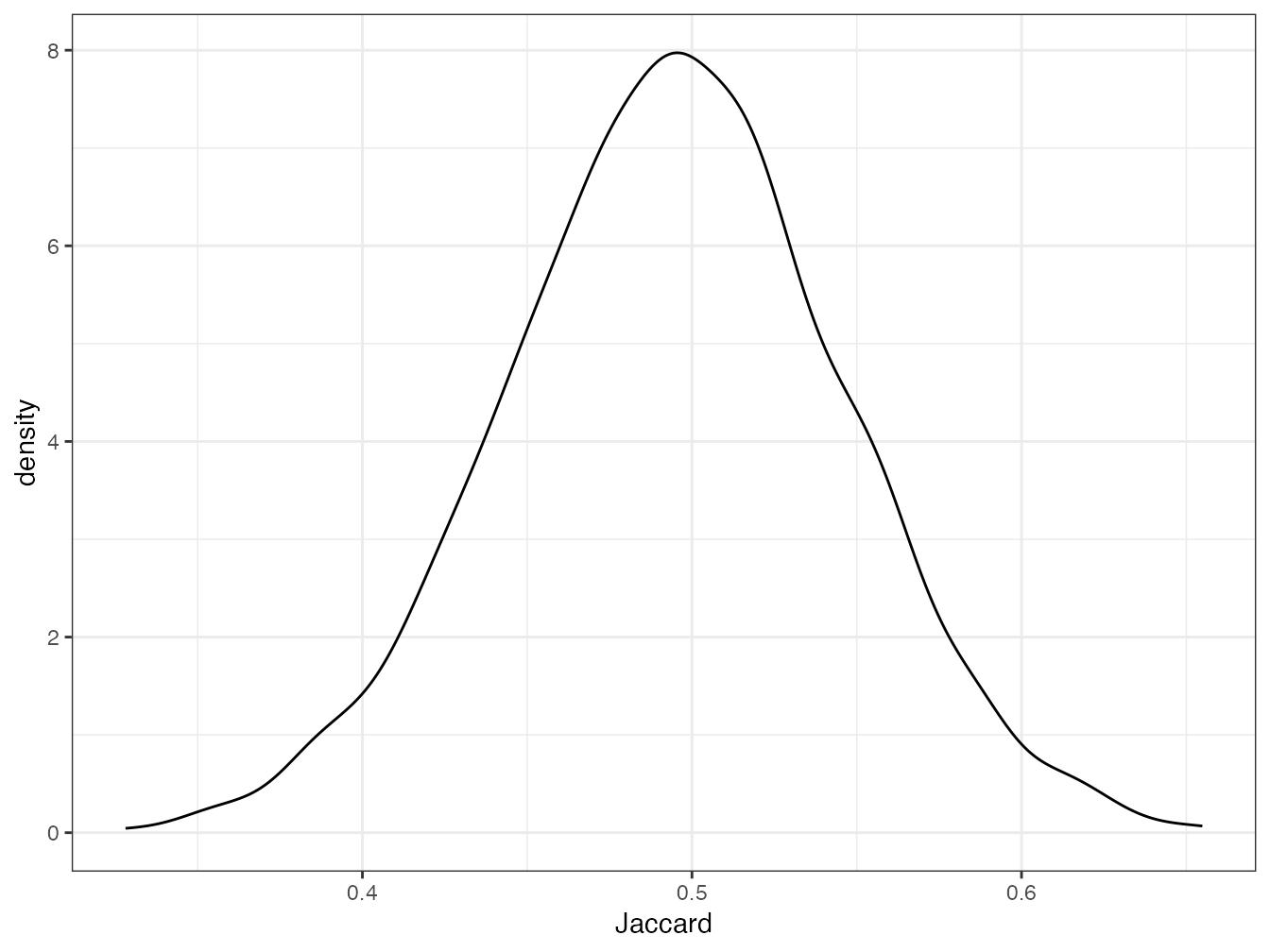
Figure 11.1: Distribution des indices de Jaccard calculés pour les 50 carrés de BCI deux à deux.

La distribution des valeurs de l’indice de Jaccard \(S_3=1-D_3^2\) est en figure 11.1. Le mode est proche de 0,5 : la moitié des espèces sont communes entre deux carrés.

Code R pour la figure :

ggplot(data.frame(Jaccard = as.numeric(1 - DistJaccard^2))) +
    geom_density(aes(x = Jaccard))

Pour afficher l’indice de Jaccard entre les carrés 1 et 2, il faut transformer la demi-matrice des distances en matrice de similarité :

Jaccard <- 1 - (as.matrix(DistJaccard))^2
Jaccard[1, 2]

## [1] 0.5663717

11.1.2 Biais d’estimation

Tous les indices de similarité vus plus haut sont sensibles au biais d’estimation. Chao et al. (2004) fournissent un estimateur de la probabilité qu’un individu de la première communauté appartienne à une espèce commune aux deux communautés :

\[\begin{equation} \tag{11.5} \hat{U} = \sum_{s}^{s_{1,1}}{\frac{n_{s,1}}{n}} + \frac{n_{+2}-1}{n_{+2}} \frac{s_1^{(2)}}{2 s_2^{(2)}} \sum_{s}^{s_{1,1}}{\frac{n_s}{n}{\mathbf 1}\left( n_{s,2}=1 \right)}. \end{equation}\]

Les sommes s’entendent pour toutes les espèces communes, indicées de 1 à \(s_{1,1}\). Le premier terme de la somme est donc la probabilité qu’un individu de la première communauté appartienne à une espèce commune aux deux communautés. \(n_{+2}\) est le nombre d’individus de la deuxième communauté. \(s_1^{(2)}\) et \(s_2^{(2)}\) sont le nombre d’espèces communes qui sont des singletons et doubletons dans la deuxième communauté. L’indicatrice \({\mathbf 1}(n_{s,2}=1)\) vaut 1 si l’espèce \(s\) est un singleton dans la deuxième communauté : la dernière somme est donc la probabilité qu’un individu de la première communauté appartienne à une espèce commune qui soit un singleton dans la deuxième communauté. S’il n’y a pas de doubletons dans la deuxième communauté, leur nombre est remplacé par 1. Enfin, il est possible que l’estimateur soit supérieur à 1, il est alors fixé à 1.

L’estimateur de la probabilité qu’un individu de la deuxième communauté appartienne à une espèce commune est noté \(\hat{V}\) et est calculé de façon symétrique à \(\hat{U}\). Le nombre d’espèces communes \(s_{1,1}\) est estimé par \(\hat{U}\hat{V}\), \(s_{1,0}\) par \((1-\hat{U})\hat{V}\) et \(s_{1,0}\) par \(\hat{U}(1-\hat{V})\). L’estimateur de l’indice de Jaccard est donc

\[\begin{equation} \tag{11.6} \hat{S}_3 = \frac{\hat{U}\hat{V}}{\hat{U}+\hat{V}-\hat{U}\hat{V}}. \end{equation}\]

L’estimateur de l’indice de Sørensen est

\[\begin{equation} \tag{11.7} \hat{S}_7 = \frac{2\hat{U}\hat{V}}{\hat{U}+\hat{V}}. \end{equation}\]

La matrice de dissimilarité corrigée est assez différente de l’originale. L’indice de Jaccard entre les deux premiers carrés devient :

# Calcul de U et V, N2Col est une matrice ou un dataframe
# de deux colonnes contenant les effectifs de chaque
# parcelle
ChaoUV <- function(N2Col) {
    NCommunity <- colSums(N2Col)
    Common <- (N2Col[, 1] > 0) & (N2Col[, 2] > 0)
    Single <- N2Col == 1
    NSingleCommon <- colSums(Common & Single)
    Double <- N2Col == 2
    NDoubleCommon <- colSums(Common & Double)
    NsCommon <- N2Col[Common, ]
    PsCommon <- t(t(NsCommon)/colSums(N2Col))
    U <- sum(PsCommon[, 1]) + (NCommunity[2] - 1)/NCommunity[2] *
        NSingleCommon[2]/2/max(NDoubleCommon[2], 1) * sum(PsCommon[,
        1][(NsCommon == 1)[, 2]])
    V <- sum(PsCommon[, 2]) + (NCommunity[1] - 1)/NCommunity[1] *
        NSingleCommon[1]/2/max(NDoubleCommon[1], 1) * sum(PsCommon[,
        2][(NsCommon == 1)[, 1]])
    return(list(U = U, V = V))
}
# Indice de Jaccard corrigé
bcJaccard <- function(N2Col) {
    ChaoEst <- ChaoUV(N2Col)
    return(min(ChaoEst$U * ChaoEst$V/(ChaoEst$U + ChaoEst$V -
        ChaoEst$U * ChaoEst$V), 1))
}
# Calcul de l'indice entre les carrés i et j de BCI, i<j.
BCIjaccard <- function(i, j) {
    if (i >= j)
        return(NA) else return(bcJaccard(t(BCI[c(i, j), ])))
}
# Calcul de la matrice de dissimilarité entre les 50 carrés
ChaoJaccard <- sapply(1:50, function(i) {
    sapply(1:50, function(j) BCIjaccard(i, j))
})
# Indice de Jaccard, carrés 1 et 2, corrigé
BCIjaccard(1, 2)

## [1] 0.9391222

La distribution des valeurs de l’indice corrigé se trouve en figure 11.2.

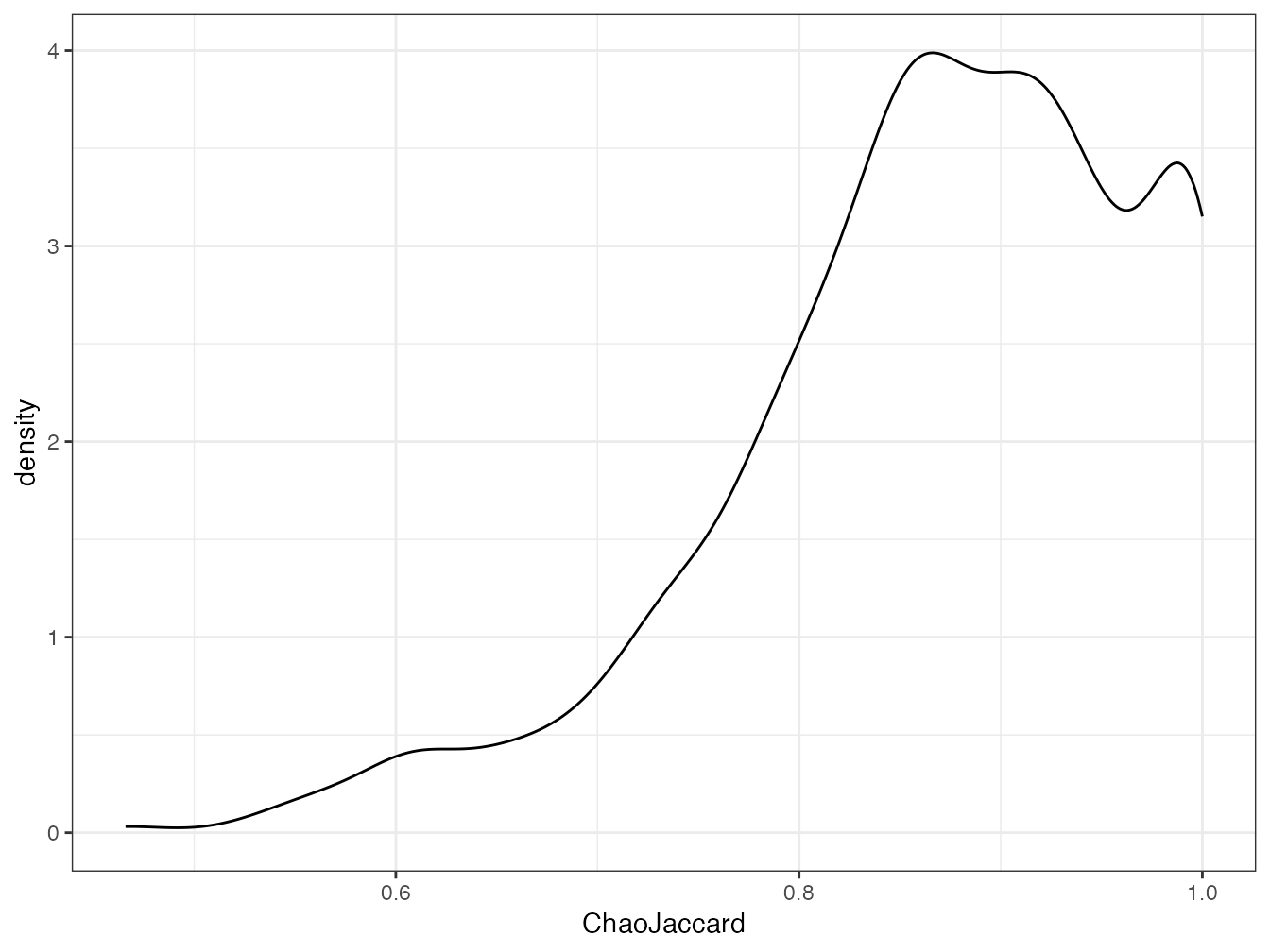
Figure 11.2: Distribution des indices de Jaccard corrigés du biais d’etimation pour les 50 carrés de BCI deux à deux.

La majorité des paires de carrés a une similarité supérieure à 0,8 après correction.

Code R pour la figure :

ggplot(data.frame(ChaoJaccard = as.numeric(ChaoJaccard))) +
  geom_density(aes(x=ChaoJaccard))

Plotkin et Muller-Landau (2002) founissent des estimateurs de la similarité de Sørensen pour les SAD les plus courantes : lognormale, broken-stick, géométrique, log-séries et même gamma, une généralisation de la distibution broken-stick. Ils traitent le cas d’un échantillonnage dans lequel les individus sont indépendants les uns des autres, et le cas de l’agrégation spatiale. Ils montrent que la similarité augmente beaucoup avec la taille des placettes échantillonnées et est nettement plus faible en cas d’agrégation spatiale.

11.1.3 Représentation graphique

La matrice de distances peut être représentée par une analyse en coordonnées principales (PCoA) (Gower 1966) :

DistChaoJaccard <- as.dist(sqrt(1 - ChaoJaccard))
PcoChaoJaccard <- dudi.pco(DistChaoJaccard, scannf = FALSE)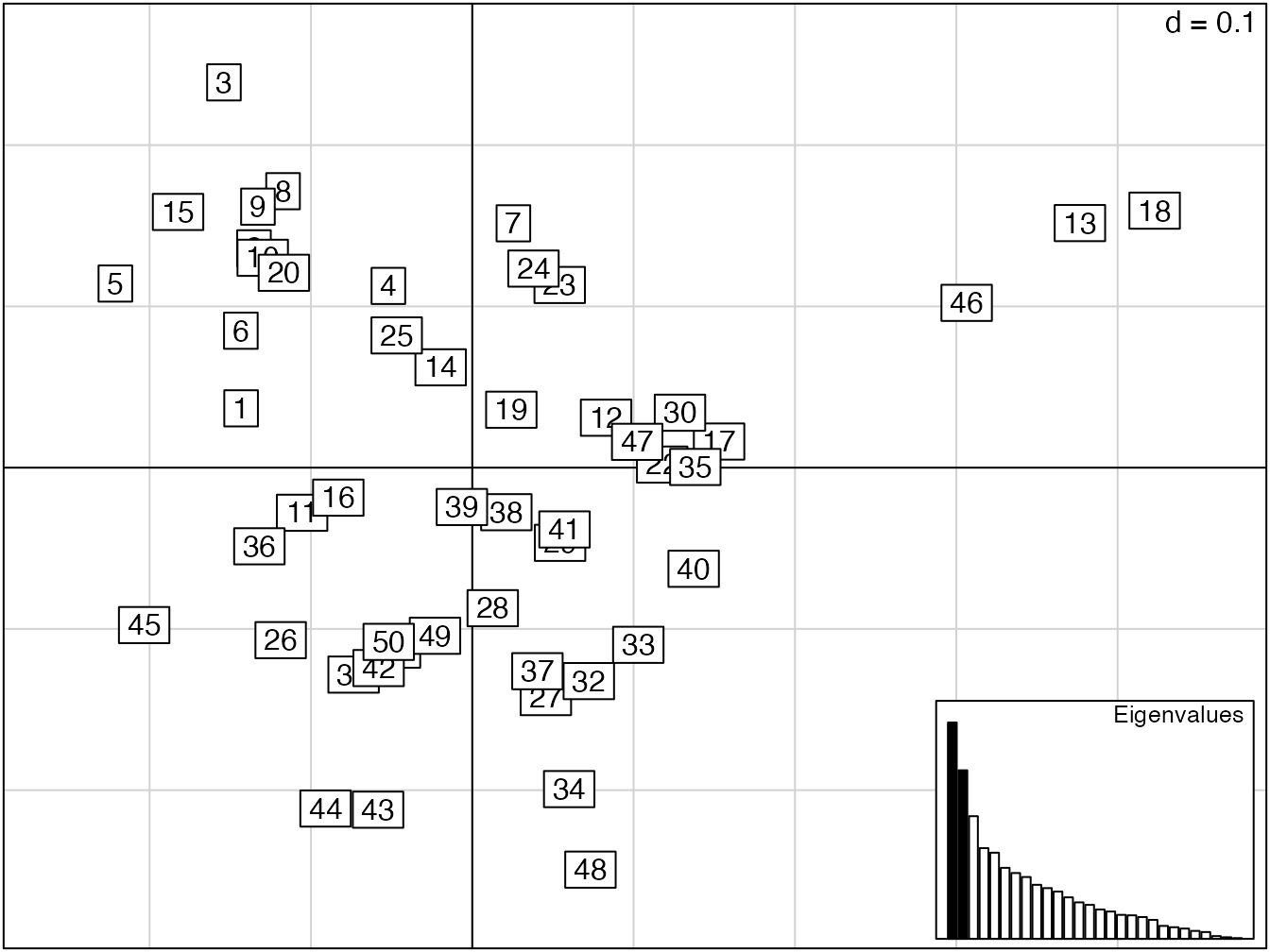

Figure 11.3: Représentation des 50 carrés de BCI dans une analyse en coordonnées principale fondée sur les distances de Jaccard.

La représentation de l’analyse est en figure 11.3. Les 50 carrés de BCI sont représentés sur le plan des deux premiers facteurs. Les valeurs propres sont représentées dans le cartouche en haut à gauche de la figure. Les distances entre les points sont les valeurs de \(\sqrt{D_3}\), projetées sur le plan. La matrice de distances n’est pas euclidienne à cause des approximations de l’estimation mais les conséquences sont faibles sur les premiers axes.

Code R pour la figure :

scatter(PcoChaoJaccard, posieig = "bottomright")

11.2 Données d’abondance

La distance la plus évidente entre communautés quand les effectifs des espèces sont connus est simplement la distance euclidienne, éventuellement normalisée par le nombre d’espèces (Dissimilarité \(D_1\) de Gower et Legendre 1986). Son problème principal est qu’elle est très sensible aux ordres de grandeurs relatifs des variables.

La dissimilarité de Steinhaus (Motyka 1947) est plus connue sous le nom de Bray-Curtis (Odum 1950; Bray et Curtis 1957), voir l’analyse historique de Legendre et Legendre (2012), note de bas de page, eq. 7.58, et pourrait être attribuée à Renkonen (1938). Elle est très utilisée, par défaut dans plusieurs analyses du package vegan par exemple :

\[\begin{equation} \tag{11.8} D_{8} = \frac{\sum_s{\left| n_{s,1}-n_{s,2} \right|}}{\sum_s{\left( n_{s,1}+n_{s,2}. \right)}} \end{equation}\]

\(n_{s,1}\) et \(n_{s,2}\) sont le nombre d’individus de l’espèce \(s\) dans la première et la deuxième communauté. La racine carrée de la dissimilarité de Bray-Curtis est euclidienne.

Gower (1971) propose une extension de la dissimilarité de Bray-Curtis : \[\begin{equation} \tag{11.9} D_{G} = \frac{\sum_s{w_s\left| n_{s,1}-n_{s,2} \right|}}{R_s\sum_s{w_s}}. \end{equation}\]

\(R_s\) est l’étendue ou l’écart-type de l’abondance de l’espèce \(s\), qui permet de ne pas surpondérer l’effet des espèces très abondantes. \(w_s\) est le poids attribué à l’espèce \(s\), qui peut être utilisé pour éliminer les doubles absences (\(w_s=0\) si l’espèce est absente des deux communautés, 1 sinon).

Anderson, Ellingsen, et McArdle (2006) proposent une mesure de dissimilarité (de Gower modifiée) donnant le même poids à une différence d’un ordre de grandeur entre les abondances qu’à la différence entre présence et absence, qui permet donc de se passer de la normalisation par \(R_s\). Les effectifs sont transformés de la façon suivante : \(x_s=\log n_s +1\) si \(n_s \ne 0\), \(x_s=1\) sinon (le logarithme est décimal). La dissimilarité est \[\begin{equation} \tag{11.10} D_{\mathit{MG}} = \frac{\sum_s{w_s\left| x_{s,1}-x_{s,2} \right|}}{\sum_s{w_s}}. \end{equation}\]

Elle n’est pas euclidienne.

Les dissimilarités de Jaccard et de Sørensen se généralisent aux données d’abondance. Le nombre d’espèces communes aux deux sites \(s_{1,1}\) est remplacé par le nombre d’individus de même espèce présents sur les deux sites : \(n_{1,1}=\sum_s{\min(n_{s,1}, n_{s,2})}\) ; le nombre d’espèces seulement présentes sur le premier site \(s_{1,0}\) est remplacé par le nombre d’individus, sommé sur toutes les espèces, présents uniquement sur le site : \(n_{1,0}=\sum_s{\max(0, n_{s,1}-n_{s,2})}\) ; de même, \(s_{0,1}\) est remplacé par \(n_{0,1}=\sum_s{\max(0, n_{s,2}-n_{s,1)}}\).

La dissimilarité de Ružička (1958) généralise celle de Jaccard :

\[\begin{equation} \tag{11.11} D_3 = 1-\frac{n_{1,1}}{n_{1,1}+n_{1,0}+n_{0,1}}. \end{equation}\]

La différence de pourcentage (percentage difference) généralise la dissimilarité de Sørensen :

\[\begin{equation} \tag{11.12} D_7 = 1- \frac{2n_{1,1}}{2n_{1,1}+n_{1,0}+n_{0,1}}. \end{equation}\]

La plupart des dissimilarités sont implémentées par la fonction dist.ldc du package adespatial.

11.3 Emboîtement et substitution

L’indice de Sørensen et les indices similaires prennent en compte deux types de dissimilarité : l’emboîtement des composition spécifiques (nestedness) et la substitution d’espèces (turnover). On parle d’emboîtement quand une communauté diffère d’une autre parce que sa composition est un sous-ensemble des espèces de l’autre. La substitution correspond au remplacement de certaines espèces d’une communauté par de nouvelles espèces. Baselga (2010b) montre que la diversité \(\beta\) de longicornes en Europe du nord est similaire à celle observée en Europe du sud, mais pour des raisons totalement différentes. En Europe du nord, les communautés perdent des espèces avec la latitude : leur dissimilarité est due principalement à l’emboîtement. En Europe du sud, les communautés sont composées d’espèces différentes : la diversité \(\beta\) est due à la substitution des espèces. Baselga décompose l’indice de dissimilarité de Sørensen, \(1-S_7\), en un terme mesurant la substitution et un mesurant l’emboîtement.

Le premier composant est l’indice de dissimilarité de G. G. Simpson (1943) : \[\begin{equation} \tag{11.13} D_{sim} = \frac{\min(s_{1,0},s_{0,1})}{s_{1,1}+\min(s_{1,0},s_{0,1})}. \end{equation}\]

Il vaut 0 quand les communautés sont emboîtées. Son complément \(D_{nes}\) prend en compte la partie de la dissimilarité due à l’emboîtement : \[\begin{equation} \tag{11.14} D_{nes} = \frac{s_{1,0} + s_{0,1}}{2s_{1,1} + s_{1,0} + s_{0,1}} - D_{sim}. \end{equation}\]

Ces mesures de dissimilarité sont généralisées au-delà de deux communautés : les formules sont disponibles dans l’article de Baselga.

Baselga (2012) étend cette décomposition à la dissimilarité de Jaccard :

\[\begin{align} \tag{11.15} D_3 &= D_{sim} + D_{nes} \\ &= \frac{2\min(s_{1,0},s_{0,1})}{s_{1,1}+2\min(s_{1,0},s_{0,1})} + \frac{s_{1,1}}{s_{1,1}+2\min(s_{1,0},s_{0,1})}\frac{|s_{1,0}-s_{0,1}|}{s_{1,1}+s_{1,0}+s_{0,1}}. \end{align}\]

Le premier terme de la somme est le terme lié à la substitution et le second celui lié à l’emboîtement.

Podani et Schmera (2011) défendent un point de vue différent sur la façon de comptabiliser les deux composantes de la décomposition de la dissimilarité de Jaccard. Le terme de substitution comptabilise les espèces présentes sur un seul site, en nombre égal : \(2\min(s_{1,0},s_{0,1})\) plutôt que l’indice de dissimilarité de Simpson. Ainsi, le terme d’emboîtement comptabilise la différence de richesse entre les deux sites : \(|s_{1,0}-s_{0,1}|\).

Après normalisation par le nombre total d’espèce, la décomposition est

\[\begin{equation} \tag{11.16} D_3 = \frac{2\min(s_{1,0},s_{0,1})}{s_{1,1} + s_{1,0} + s_{0,1}} + \frac{|s_{1,0}-s_{0,1}|}{s_{1,1} + s_{1,0} + s_{0,1}}. \end{equation}\]

La controverse entre les deux décompositions perdure (Podani et Schmera 2016).

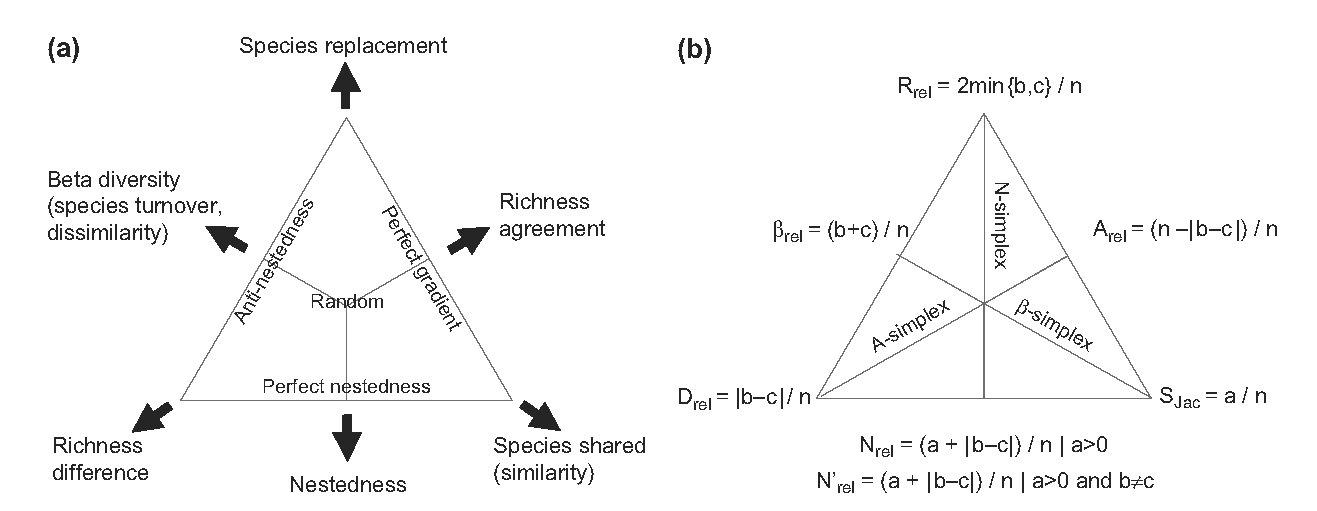
Figure 11.4: Triangle du simplex Similarité-Substitution-Emboîtement. (a) Similarité, emboîtement et substitution somment à 1 donc les trois composantes peuvent être représentées dans un triangle et combinées deux à deux. La dissimilarité est par exemple représentée par la proximité au côté gauche du triangle, somme de l’emboîtement et de la substitution (ses sommets adjacents) et complément à 1 de la dissimilarité (le sommet opposé). (b) Les formules de calcul dont données pour la similarité de Jaccard. Avec ces notations classiques, \(a\) est le nombre d’espèces communes \(s_{1,1}\), \(b\) et \(c\) sont les espèces propres à chaque communauté, \(s_{0,1}\) et \(s_{1,0}\), et \(n\) est le nombre total d’espèces \(a+b+c\).

Comme la dissimilarité est la somme de l’emboîtement et de la substitution et que la dissimilarité est le complément à 1 de la similarité, la somme de la similarité, de l’emboîtement et de la substitution vaut 1. Podani et Schmera (2011) représentent cette égalité dans un triangle dont les sommets correspondent aux trois termes (Figure 11.4).

Podani, Ricotta, et Schmera (2013) étendent cette approche à des mesures de dissimilarité prenant en compte les abondances, particulièrement la dissimilarité de Ružička. La décomposition est identique à celle de l’équation (11.16) après remplacement de chaque terme.

Legendre (2014) considère cette décomposition de la diversité \(\beta\) en emboîtement et substitution comme une décomposition de variance et lui applique des méthodes d’ordination pour la relier aux variables environnementales par exemple.

Les mesures de diversité \(\beta\) fondées sur l’entropie HCDT (chapitre 12) ne permettent pas de distinguer directement emboîtement et substitution. La variabilité des contributions \(^{q}_{i}\!H_{\beta}\) des communautés à l’entropie \(\beta\) augmente avec l’emboîtement, mais cette voie n’a pas été explorée.

11.4 Données d’abondance et similarité des espèces

11.4.1 Dissimilarité minimale moyenne

Ricotta et Bacaro (2010) définissent une mesure de dissimilarité paramétrique entre deux communautés. Une matrice de dissimilarité est définie entre toutes les paires d’espèces. \(\min{d_{s,2}}\) désigne la dissimilarité entre l’espèce \(s\) présente dans la première communauté et l’espèce la plus proche d’elle dans la deuxième communauté. \(\min{d_{t,1}}\) est la même notation pour l’espèce \(t\) de la deuxième communauté et l’espèces la plus proche dans la communauté 1. Ces valeurs sont nulles pour toutes les espèces communes.

\(\pi_{s(n)}\) désigne la contribution de l’espèce \(s\) à l’indice de Hurlbert, déjà vue dans le cadre de l’originalité taxonomique (Section 7.2.2). La contribution des espèces rares augmente avec le paramètre \(n\) (figure 7.3). Pour chaque communauté, la moyenne des dissimilarités minimales entre chaque espèce et l’autre communauté est calculée, pondérée par la contribution de l’espèce à l’indice de Hurlbert.

La dissimilarité pondérée (W pour weighted) entre les deux communautés (C pour community) en est la moyenne entre les deux communautés : \[\begin{equation} \tag{11.17} d_{\mathit{CW}(n)} = \frac{1}{2}\left(\sum_s{\pi_{s(n)} \min{d_{s,2}}} + \sum_t{\pi_{t(n)} \min{d_{t,1}}} \right). \end{equation}\]

Sa version non pondérée (U pour unweighted) par les abondances est (Ricotta et Burrascano 2008) \[\begin{equation} \tag{11.18} d_{\mathit{CU}} = \frac{\sum_s{\min{d_{s,2}}} + \sum_t{\min{d_{t,1}}}}{2s_{1,1}+s_{1,0}+s_{0,1}}. \end{equation}\]

Ces mesures sont des évolutions de mesures plus anciennes, avec des pondérations différentes. Dans l’indice de Clarke et Warwick (1998), la moyenne est calculée dans chaque communauté, sans pondération : \[\begin{equation} \tag{11.19} d_{\mathit{CW}} = \frac{1}{2}\left( \frac{\sum_s{\min{d_{s,2}}}}{s_{1,1}+s_{1,0}} + \frac{\sum_t{\min{d_{t,1}}}}{s_{1,1}+s_{0,1}} \right), \end{equation}\]

mais avec pondération par l’abondance des espèces chez Ricotta et Burrascano (2008) : \[\begin{equation} \tag{11.20} d_{\mathit{RB}} = \frac{1}{2}\left( \sum_s{p_{s|1}\min{d_{s,2}}} + \sum_t{p_{t|2}\min{d_{t,1}}} \right), \end{equation}\]

alors qu’elle l’est globalement dans l’indice de Izsak et Price (2001) : \[\begin{equation} \tag{11.21} d_{\mathit{IP}} = \frac{\sum_s{\min{d_{s,2}}} + \sum_t{\min{d_{t,1}}}}{s_{1,1}+s_{1,0}+s_{1,1}+s_{0,1}}, \end{equation}\]

redécouvert et nommé COMDISTNN par Webb, Ackerly, et Kembel (2008).

11.4.2 Similarité moyenne entre individus

Pavoine et Ricotta (2014) définissent une famille de similarités entre communautés construite à partir de la similarité moyenne entre les paires d’individus de chaque communauté et les paires intercommunautaires. Une matrice de similarité \(\mathbf{Z}\) est définie entre les paires d’espèces : \(z_{s,t}\) est la similarité entre l’espèce \(s\) et l’espèce \(t\), comprise entre 0 et 1 de la même façon que pour le calcul de la diversité \(^q\!D^{\mathbf{Z}}\) (chapitre 9). La matrice \(\mathbf{Z}\) doit de plus être semi-définie positive, ce qui implique que \(\sqrt{1-\mathbf{Z}}\) est euclidienne : de cette façon, les espèces peuvent être représentées graphiquement par une PCoA. Les fréquences des espèces dans les deux communautés sont \(\mathbf{p}\) et \(\mathbf{q}\). La similarité moyenne dans chaque communauté est \(\sum_{s,t}{p_s p_t z_{s,t}}\) et \(\sum_{s,t}{q_s q_t z_{s,t}}\). La similarité moyenne des paires d’individus de communautés différentes est \(\sum_{s,t}{p_s q_t z_{s,t}}\).

La dissimilarité entre communautés de Rao (Section 12.5) peut être normalisée (en la divisant par sa valeur maximale pour qu’elle soit comprise entre 0 et 1) puis transformée en similarité (en prenant son complément à 1) pour obtenir

\[\begin{equation} \tag{11.22} S_{\mathit{Sorensen}} = \frac{\sum_{s,t}{p_s q_t z_{s,t}}}{\frac{1}{2}\sum_{s,t}{p_s p_t z_{s,t}} + \frac{1}{2}\sum_{s,t}{q_s q_t z_{s,t}}}. \end{equation}\]

Les probabilités peuvent être remplacées par n’importe quel vecteur de valeurs positives, par exemple les abondances ou des valeurs 1 et 0 pour des données de présence-absence. Dans ce dernier cas, et si \(\mathbf{Z}\) est la matrice identité \(\mathbf{I}\) (la similarité de deux espèces différentes est nulle et \(z_{s,s}=1\)), \(S_{\mathit{Sorensen}}\) se réduit à l’indice de Sørensen vu plus haut.

La généralisation de l’indice de Jaccard aux données d’abondances est

\[\begin{equation} \tag{11.23} S_{\mathit{Jaccard}} = \frac{\sum_{s,t}{p_s q_t z_{s,t}}}{\sum_{s,t}{p_s p_t z_{s,t}} + \sum_{s,t}{q_s q_t z_{s,t}} - \sum_{s,t}{p_s q_t z_{s,t}}}. \end{equation}\]

Il se réduit à l’indice de Jaccard original pour les données de présence-absence et \(\mathbf{Z} = \mathbf{I}\).

L’indice de Sokal et Sneath se généralise par

\[\begin{equation} \tag{11.24} S_{\mathit{Sokal}} = \frac{\sum_{s,t}{p_s q_t z_{s,t}}}{2 \sum_{s,t}{p_s p_t z_{s,t}} + 2 \sum_{s,t}{q_s q_t z_{s,t}} - 3 \sum_{s,t}{p_s q_t z_{s,t}}}, \end{equation}\]

celui d’Ochiai par :

\[\begin{equation} \tag{11.25} S_{\mathit{Ochiai}} = \frac{\sum_{s,t}{p_s q_t z_{s,t}}}{\sqrt{\sum_{s,t}{p_s p_t z_{s,t}}} \sqrt{\sum_{s,t}{q_s q_t z_{s,t}}}}. \end{equation}\]

Ces quatre similarités permettent une représentation des communautés par PCoA de la même façon que l’indice de Jaccard traité plus haut.

Ricotta, Bacaro, et Pavoine (2014) ont aussi proposé de mesurer la dissimilarité par la somme des différences (en valeur absolue) de banalité des espèces des deux communautés, normalisée par la banalité totale : \[\begin{equation} \tag{11.26} D_{\mathit{RBP}} = \frac{\sum_{s}{|\sum_{t}{(p_s-q_t)z_{s,t}}}|}{\sum_{s}{\sum_{t}{(p_s+q_t)z_{s,t}}}}. \end{equation}\]

D’autres similarités ont été proposées mais ont des propriétés qui empêchent de les utiliser (Ricotta, Bacaro, et Pavoine 2014) : leur valeur n’est pas toujours nulle pour deux communautés identiques. Ce sont l’indice proposé par Rao (1982), \[\begin{equation} \tag{11.27} Q_{\mathit{12}} = \sum_{s,t}{p_s q_t z_{s,t}}, \end{equation}\]

comme les indices de Swenson, Anglada-Cordero, et Barone (2011) : \[\begin{equation} \tag{11.28} d_{\mathit{pw}} = \frac{1}{2}\left( \frac{\sum_s{\bar{d_{s,2}}}}{s_{1,1}+s_{1,0}} + \frac{\sum_t{\bar{d_{t,1}}}}{s_{1,1}+s_{0,1}} \right), \end{equation}\]

et \[\begin{equation} \tag{11.29} d_{\mathit{pw}}' = \frac{1}{2}\left( \sum_s{p_s\bar{d_{s,2}}} + \sum_t{q_t\bar{d_{t,1}}} \right), \end{equation}\]

où \(\bar{d_{s,2}}\) est la dissimilarité moyenne entre l’espèce \(s\) de la communauté 1 et toutes les espèces de la communauté 2.

11.5 Distance entre paires de communautés et diversité \(\beta\) proportionnelle

Dans certains cas présentés ici, la diversité de différentiation est parfaitement conciliable avec la diversité proportionnelle.

11.5.1 Diversité de Simpson

ter Braak (1983) a le premier rapproché l’entropie de Simpson et l’Analyse en Composantes Principales (Pearson 1901). En représentant les communautés dans l’espace des espèces, la norme du vecteur de la communauté \(i\) est \({\sum_s{p_{s|i}^2}}\), c’est-à-dire 1 moins l’entropie de Simpson. La représentation graphique de l’ACP (non centrée, non réduite) montre les communautés les moins diverses (les plus éloignées de l’origine du repère). Ter Braak définit la diversité \(\beta\) comme la distance entre deux communautés (et la moyenne des distances entre paires de communautés si leur nombre est supérieur à 2). Cette “définition” est valide puisque cette distance est la composante inter de la décomposition de l’entropie \(\beta\) de Simpson (12.11).

Figure 11.5: Représentation des deux premiers axes factoriels de l’ACP des 50 carrés de BCI. Les données sont les probabilités des espèce, ni centrées ni réduites pour l’ACP. Les carrés sont représentés avec les espèces. Les carrés 35 et 40 ont une diversité faible et sont associés aux espèces Gustavia superba et Alseis blackiana.

L’ACP non centrée des 50 carrés de BCI est en figure 11.5.

Code R pour la figure :

pcaBCI <- dudi.pca(BCI/rowSums(BCI), scannf = FALSE, nf = 2,
    center = FALSE, scale = FALSE)
scatter(pcaBCI, posieig = "bottomleft")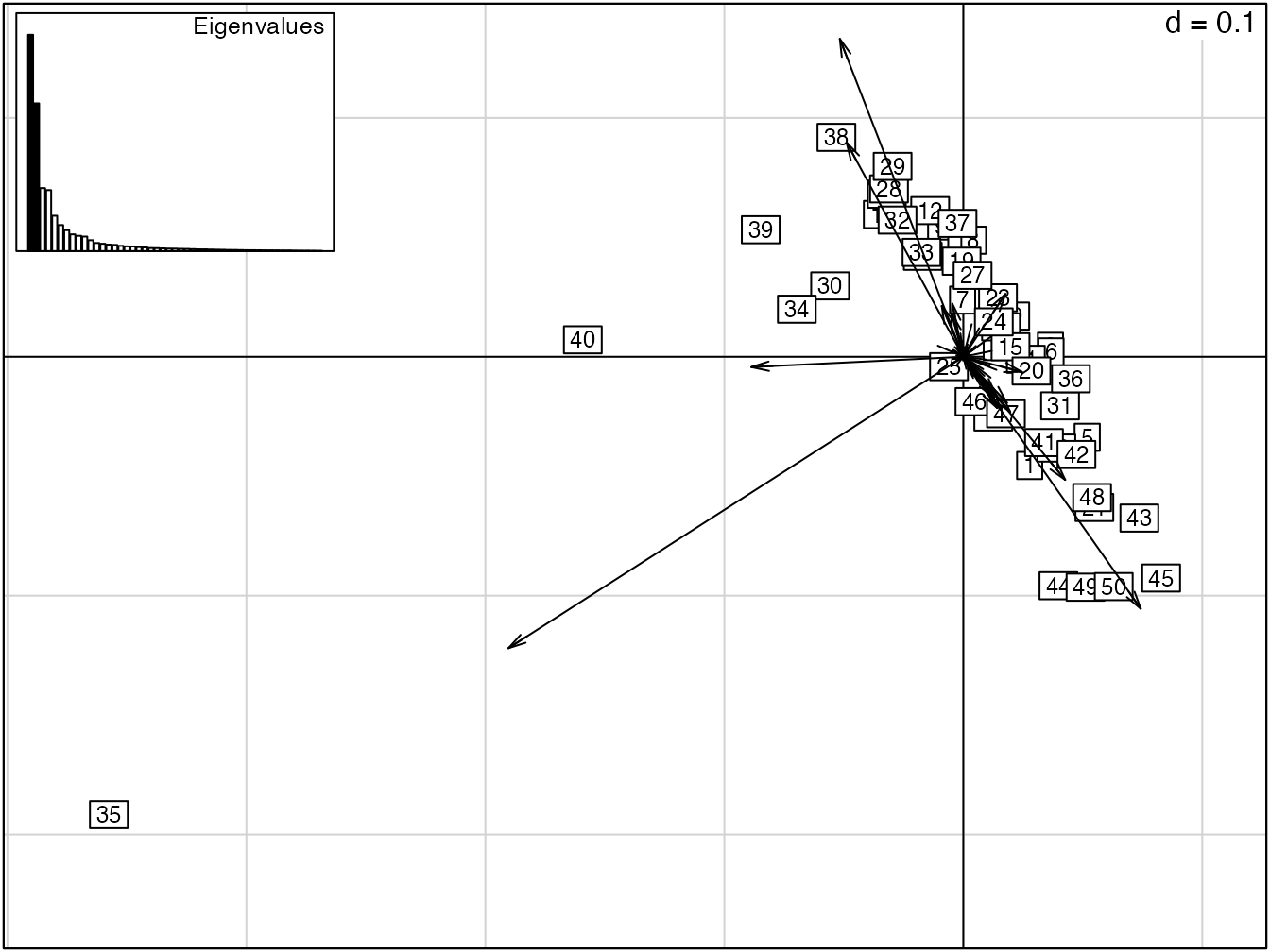

Figure 11.6: ACP centrée des 50 carrés de BCI pour visualiser la diversité \(\beta\).

L’ACP centrée (mais non réduite, figure 11.6) permet de mieux représenter la diversité \(\beta\) : la distance de chaque carré au centre du repère est sa contribution.

Code R :

pcaBCI <- dudi.pca(BCI/rowSums(BCI), scannf = FALSE, nf = 2,
    center = TRUE, scale = FALSE)
scatter(pcaBCI, clab.col = 0)

11.5.2 Généralisation

Legendre et Anderson (1999) ont montré plus largement que si les communautés sont représentées dans l’espace vectoriel des espèces, la moyenne des carrés des distances euclidiennes entre communautés égale la somme des carrés des écarts à la moyenne des distributions des espèces :

\[\begin{equation} \tag{11.30} \frac{1}{I} \sum_{i=1}^{I-1}{\sum_{j=i+1}^{I}{d_{i,j}^2}} = \sum_{s=1}^{S}{\sum_{i=1}^{I}{\left(y_{s|i}-y_s \right)^2}}. \end{equation}\]

\(y_{s|i}\) peut être le nombre d’individus \(n_{s,i}\) ou la probabilité \(p_{s|i}\). Les communautés ont ici le même poids, \(y_s\) est la moyenne des valeurs de l’espèce \(s\) dans chaque communauté. La somme des carrés des écarts est une mesure de diversité \(\beta\). Si \(y_{s|i}\) est la probabilité \(p_{s|i}\), il s’agit de l’entropie \(\beta\) de Simpson.

Ce résultat peut être étendu à toute matrice de distances euclidiennes entre communautés (Legendre, Borcard, et Peres-Neto 2005) : l’argument est qu’il existe une matrice de \(y_{s|i}\), transformation des \(p_{s|i}\), telle que la distance entre les communautés est cette matrice de distances. La moyenne des dissimilarités \(D_n\) ou des compléments à 1 des similarités de Pavoine et Ricotta (qui sont les carrés des distances euclidiennes de la PCoA) est donc une mesure de diversité \(\beta\).

Pour un certain nombre de distances, la transformation de \(p_{s|i}\) en \(y_{s|i}\) est bien connue (Legendre et Gallagher 2001).

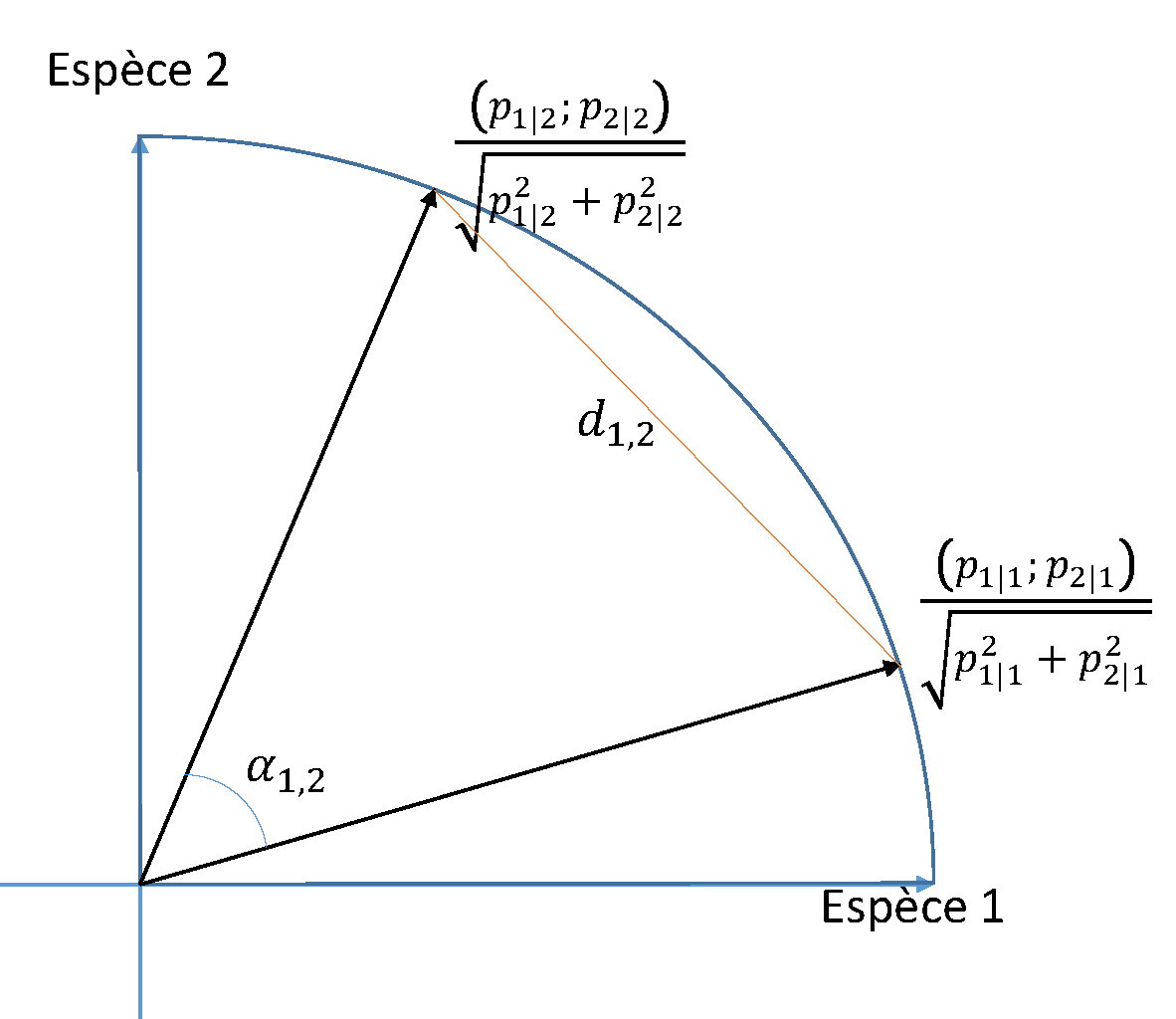
Figure 11.7: Distance de corde entre deux communautés représentées dans l’espace engendré par deux espèces. La distance \(d_{1,2}\) entre les deux communautés est la longueur de la corde qui relie leurs vecteurs de composition normalisés sur le cercle de rayon 1. C’est aussi deux fois le sinus de l’angle \({\alpha_{1,2}}/{2}\) formé par les deux vecteurs de composition des communautés.

La distance de corde (Figure 11.7) est obtenue par la transformation

\[\begin{equation} \tag{11.31} y_{s|i} = \frac{p_{s|i}}{\sqrt{\sum_s{p_{s|i}^2}}}. \end{equation}\]

Les communautés sont représentées dans l’espace des espèces par un vecteur dont les composantes sont proportionnelles aux probabilités des espèces mais dont la norme est 1. La distance entre communautés est donc la longueur de la corde qui relie les extrêmités de leurs vecteurs sur la sphère à \(S\) dimensions de rayon 1.

La distance de Hellinger est obtenue par \[\begin{equation} \tag{11.32} y_{s|i} = \sqrt{p_{s|i}}. \end{equation}\]

La distance euclidienne entre les profils de communautés (\(y_{s|i} = p_{s|i}\)) utilisée par ter Braak (1983) n’est pas optimale parce qu’elle souffre des défauts de l’entropie de Simpson (Jost 2007) qu’elle représente. Legendre et De Cáceres (2013), annexe S3, ont établi une liste de bonnes propriétés que doivent respecter les mesures de distance entre communautés pour analyser la diversité de différentiation. La fonction dist.ldc du package adespatial permet de calculer toutes les distances présentées dans l’article. Les distance de corde et de Hellinger (qui est la distance entre les racines carrées des profils de communautés) les respectent toutes.

La diversité \(\beta\) exprimée de cette façon peut faire l’objet d’analyses par les méthodes d’ordination classiques (RDA : Analyse de Redondance (Rao 1964) ; CCA : Analyse Canonique de Correspondance (ter Braak 1986)) pour la relier à des variables environnementales par exemple(Legendre et De Cáceres 2013).

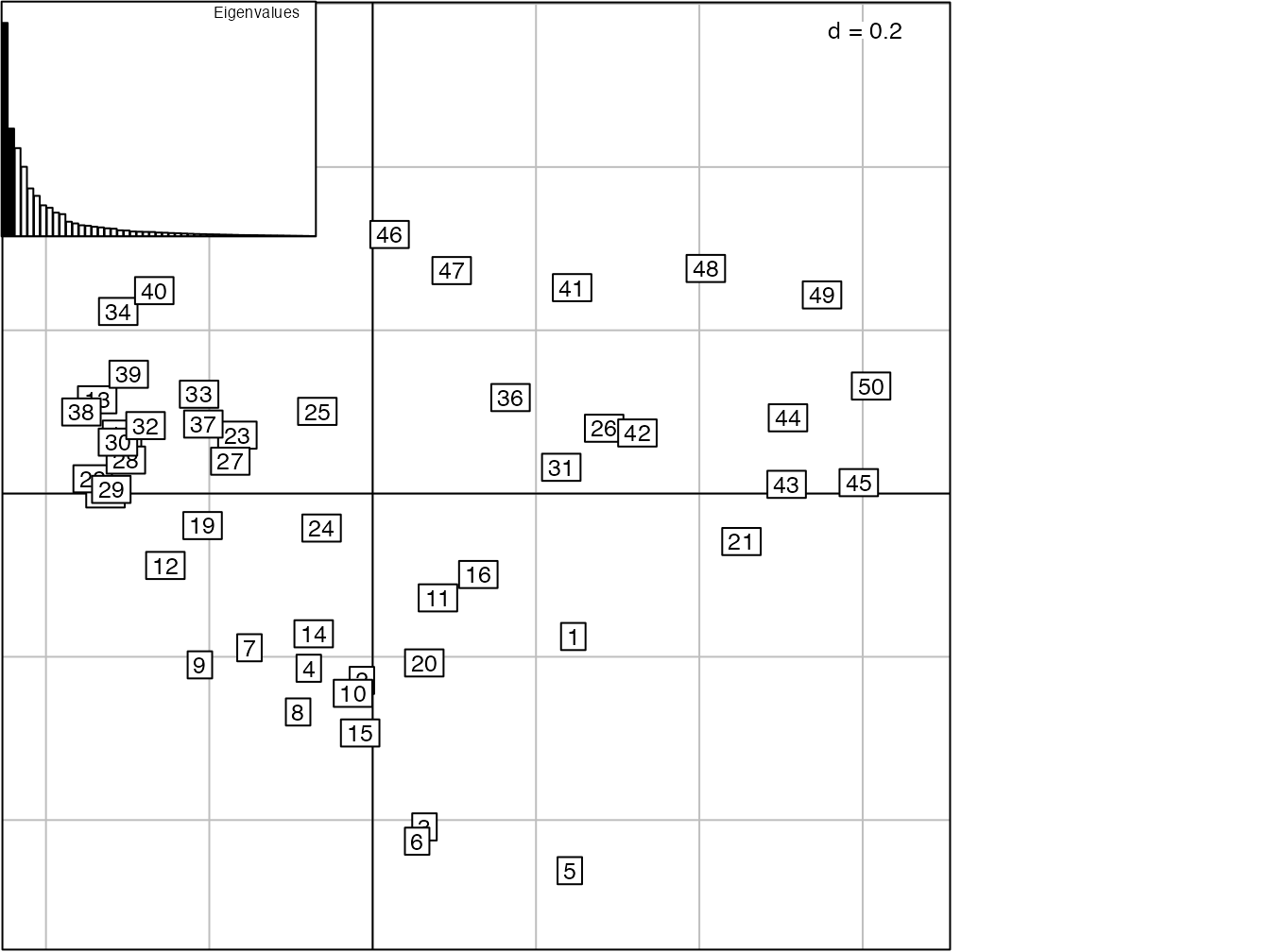
Figure 11.8: PCoA appliquée à la distance de corde des 50 carrés de BCI pour visualiser la diversité \(\beta\).

La diversité \(\beta\) de BCI (figure 11.6) est mieux représentée par une analyse en coordonnées principales appliquée à la distance de corde entre les communautés (figure 11.8). La limite de la méthode est que l’origine du repère ne représente plus ici la méta-communauté : sa position correspond à la moyenne des probabilités des espèces transformées, \(y_{s|i}\), pas à celle des \(p_{s|i}\).

Code R :

library("adespatial")
dCorde <- dist.ldc(BCI, method = "chord")
pcoaBCI <- dudi.pco(dCorde, scannf = FALSE, nf = 2)
scatter(pcoaBCI)

11.6 Tests de significativité

11.6.1 Test de non-nullité

Chase et al. (2011) testent la valeur de diversité \(\beta\) observée contre sa valeur attendue sous l’hypothèse nulle d’une distribution aléatoire des individus dans les communautés.

Leur motivation principale est d’éliminer la dépendance de la diversité \(\beta\) à la diversité \(\alpha\) due à la mesure de diversité qu’ils utilisent : l’indice de Jaccard, appliqué aux données de présence-absence. Des communautés théoriques sont tirées selon le modèle nul (selon une distribution multinomiale correspondant aux probabilités des espèces dans la méta-communauté et la taille de chaque communauté dans le cas le plus courant). La distribution de la diversité \(\beta\) sous l’hypothèse nulle est obtenue en répétant les simulations. La différence entre la diversité \(\beta\) réelle et la moyenne simulée est normalisée par la moyenne simulée pour obtenir une valeur comprise entre -1 et +1 (l’indice de Jaccard est compris entre 0 et 1), comparée à sa distribution sous l’hypothèse nulle pour évaluer sa significativité.

Tucker et al. (2016) étendent cette méthode aux données d’abondance en utilisant la dissimilarité de Bray-Curtis et testent, à partir de communautés simulées, sa capacité à distinguer les mécanismes d’assemblage des communautés : niche contre modèle neutre, et modèles déterministes contre stochastiques (c’est-à-dire dont les paramètres varient aléatoirement). Ces deux oppositions peuvent être traitées indépendamment, pour éviter la confusion entre niche et déterminisme et entre neutralité et stochasticité. Ils concluent qu’une valeur de diversité \(\beta\) significativement différente de celle du modèle nul permet de détecter le mécanisme de niche (alors que le modèle neutre donne une valeur identique à celle de l’hypothèse nulle, 0 étant donné la normalisation). Chase et Myers (2011) interprétait les valeurs significatives comme preuve de déterminisme (par opposition à la stochasticité). Tucker et al. montrent que ce n’est pas le cas : le niveau de stochasticité influe peu sur les résultats quand la diversité est mesurée à partir de données d’abondance. En revanche, la méthode n’est pas fiable quand elle est utilisée avec des données de présence-absence : la stochasticité ne permet alors plus de distinguer les mécanismes.

11.6.2 Analyse de la variabilité

Anderson, Ellingsen, et McArdle (2006) fournissent un test d’égalité de la diversité \(\beta\) entre groupes de communautés. Les communautés sont placées dans un espace euclidien, dans lequel les distances entre elles sont une mesure de dissimilarité présentée dans ce chapitre. Si les dissimilarités ne sont pas euclidiennes, une PCoA permet de les placer dans un espace euclidien dont certains axes sont imaginaires, sans que cette difficulté invalide la méthode.

Dans chaque groupe, la distance entre chaque communauté et le centre de gravité du groupe est calculée. Une Anova est réalisée à partir de ces distances. La statistique F de l’Anova suit une loi de Fisher si la distribution des distances aux centres de gravité est normale. Si ce n’est pas le cas, le test peut être réalisé par permutation des distances entre les groupes. La statistique de test de l’Anova est le rapport de la dispersion des centres de gravité des groupes à celle des dispersion des communautés dans chaque groupe. Elle est comparée à sa distribution obtenue par permutation.

Une alternative consiste à utiliser la distance aux médianes spatiales des groupes. La médiane spatiale est le point qui minimise la somme des distances entre les points et lui (alors que le centre de gravité minimise la somme des carrés de ces distances).

La fonction betadisper du package vegan implémente ce test.

Ricotta et Burrascano (2009) utilisent comme point central de chaque groupe celui représentant l’assemblage de ses communautés. Ils définissent ainsi la diversité \(\beta\) comme la dissimilarité moyenne entre chaque communauté et la méta-communauté.

Bacaro, Gioria, et Ricotta (2012) préfèrent tester la distribution des dissimilarités entre paires des communautés plutôt que la dissimilarité entre chaque communauté et un point de référence. Une statistique F est calculée à partir de ces dissimilarités et comparée à sa distribution obtenue par permutation. La méthode de permutation originale est inappropriée et donc corrigée (Bacaro, Gioria, et Ricotta 2013) : les dissimilarités doivent être redistribuées aléatoirement entre les groupes.