1 Notions de Diversité

1.1 Composantes

Figure 1.1: Importance de la richesse (en haut) et de l’équitabilité (en bas) pour la définition de la diversité. Ligne du haut : toutes choses égales par ailleurs, une communauté de 7 espèces semble plus diverse qu’une communauté de 2 espèces. Ligne du bas : à richesse égale, une communauté moins équitable (à gauche) semble moins diverse. Colonne de gauche : une communauté moins riche (en haut) peut sembler plus diverse si elle est plus équitable. Colonne de droite : idem pour la communauté du bas.

Une communauté comprenant beaucoup d’espèces mais avec une espèce dominante n’est pas perçue intuitivement comme plus diverse qu’une communauté avec moins d’espèces, mais dont les effectifs sont proches (figure 1.1, colonne de gauche). La prise en compte de deux composantes de la diversité, appelées richesse et équitabilité, est nécessaire (Whittaker 1965).

1.1.1 Richesse

La richesse (terme introduit par Mcintosh 1967) est le nombre (ou une fonction croissante du nombre) de classes différentes présentes dans le système étudié, par exemple le nombre d’espèces d’arbres dans une forêt.

Un certain nombre d’hypothèses sont assumées plus ou moins explicitement :

• Les classes sont bien connues : compter le nombre d’espèces a peu de sens si la taxonomie n’est pas bien établie. C’est parfois une difficulté majeure quand on travaille sur les microorganismes ;
• Les classes sont équidistantes : la richesse augmente d’une unité quand on rajoute une espèce, que cette espèce soit proche des précédentes ou extrêmement originale.

L’indice de richesse le plus simple et le plus utilisé est tout simplement le nombre d’espèces \(S\).

1.1.2 Équitabilité

La régularité de la distribution des espèces (équitabilité en Français, evenness ou equitability en anglais) est un élément important de la diversité. Une espèce représentée abondamment ou par un seul individu n’apporte pas la même contribution à l’écosystème. Sur la figure 1.1, la ligne du bas présente deux communautés de 4 espèces, mais celle de droite est beaucoup plus équitable de celle de gauche et semble intuitivement plus diverse. À nombre d’espèces égal, la présence d’espèces très dominantes entraîne mathématiquement la rareté de certaines autres : on comprend donc assez intuitivement que le maximum de diversité sera atteint quand les espèces auront une répartition très régulière.

Un indice d’équitabilité est indépendant du nombre d’espèces (donc de la richesse).

La plupart des indices courants, comme ceux de Simpson ou de Shannon, évaluent à la fois la richesse et l’équitabilité.

1.1.3 Disparité

Les mesures classiques de la diversité, dites mesures de diversité neutre (species-neutral diversity) ou taxonomique ne prennent pas en compte une quelconque distance entre classes. Pourtant, deux espèces du même genre sont de toute évidence plus proches que deux espèces de familles différentes. Les mesures de diversité non neutres (chapitre 6) prennent en compte cette notion, qui nécessite quelques définitions supplémentaires (Mouillot, Stubbs, et al. 2005; Ricotta 2007).

La mesure de la différence entre deux classes est souvent une distance, mais parfois une mesure qui n’a pas toutes les propriétés d’une distance : une dissimilarité. Les mesures de divergence (Pavoine et Bonsall 2011) sont construites à partir de la dissimilarité entre les classes, avec ou sans pondération par la fréquence.

Si la divergence entre espèces est une distance évolutive comme l’âge du plus récent ancêtre commun, la diversité sera dite phylogénétique. Si c’est une distance fonctionnelle, définie par exemple dans l’espace des traits fonctionnels, la diversité sera dite fonctionnelle.

La disparité (Runnegar 1987), divergence moyenne entre deux espèces (indépendamment des fréquences), ou de façon équivalente la longueur totale des branches d’un arbre phylogénétique, est la composante qui décrit à quel point les espèces sont différentes les unes des autres.

Les mesures de régularité décrivent la façon dont les espèces occupent l’espace des niches (régularité fonctionnelle) ou la régularité dans le temps et entre les clades des évènements de spéciation représentés par un arbre phylogénétique. Ce concept complète celui d’équitabilité dans les mesures classiques : la diversité augmente avec la richesse, la divergence entre espèces, et la régularité (qui se réduit à l’équitabilité quand toutes les espèces sont également divergentes entre elles).

1.1.4 Agrégation

À partir d’une large revue de la littérature dans plusieurs disciplines scientifiques s’intéressant à la diversité (au-delà de la biodiversité), A. Stirling (2007) estime que les trois composantes, qu’il nomme variété (richesse), équilibre (équitabilité) et disparité, recouvrent tous les aspects de la diversité.

Stirling définit la propriété d’agrégation comme la capacité d’une mesure de diversité à combiner explicitement les trois composantes précédentes. Cela ne signifie pas que les composantes contribuent indépendamment les unes des autres à la diversité (Jost 2010b).

1.2 Niveaux de l’étude

La diversité est classiquement estimée à plusieurs niveaux emboîtés, nommés \(\alpha\), \(\beta\) et \(\gamma\) par Whittaker (1960, 320) qui a nommé \(\alpha\) la diversité locale qu’il mesurait avec l’indice \(\alpha\) de Fisher (voir le chapitre 20) et a utilisé les lettres suivantes selon ses besoins.

1.2.1 Diversité \(\alpha\), \(\beta\) et \(\gamma\)

La diversité \(\alpha\) est la diversité locale, mesurée à l’intérieur d’un système délimité. Plus précisément, il s’agit de la diversité dans un habitat uniforme de taille fixe.

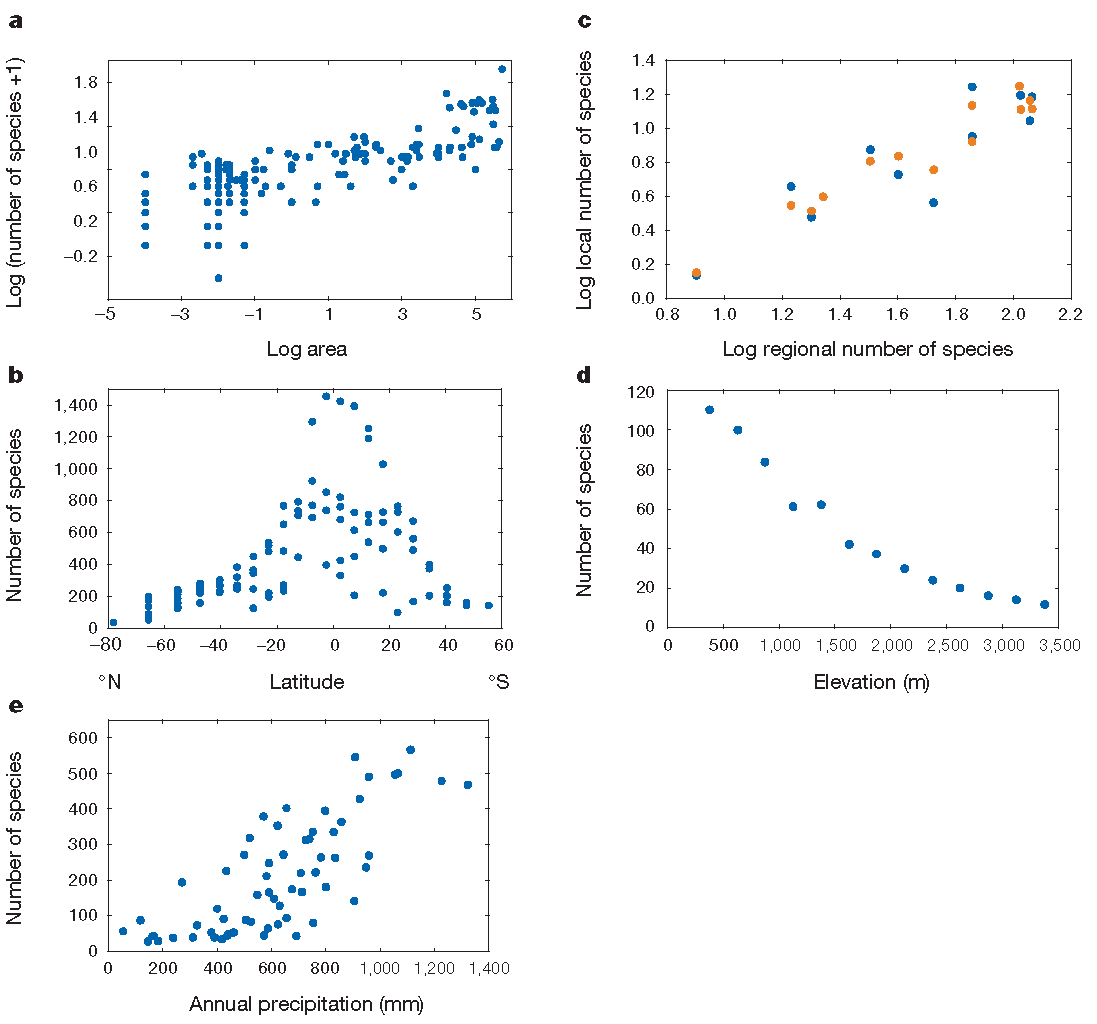
Figure 1.2: Patrons de biodiversité. (a) Le nombre d’espèces de vers de terre augmente en fonction de la surface échantillonnée, de 100 m² à plus de 500000 km² selon la relation d’Arrhenius). (b) Nombre d’espèces d’oiseaux en fonction de la latitude. (c) Relation entre la richesse régionale et la richesse locale. (d) Nombre d’espèces de chauves-souris en fonction de l’altitude dans une réserve au Pérou. (e) Nombre d’espèces de végétaux ligneux en fonction des précipitations en Afrique du Sud.

De façon générale (Gaston 2000), la richesse spécifique diminue avec la latitude (la diversité est plus grande dans les zones tropicales, et au sein de celles-ci, quand on se rapproche de l’équateur), voir figure 1.2 (Gaston 2000, fig. 1). La tendance est la même pour la diversité génétique intraspécifique (Miraldo et al. 2016). La richesse diminue avec l’altitude. Elle est généralement plus faible sur les îles, où elle décroît avec la distance au continent, source de migrations.

La diversité \(\beta\) mesure à quel point les systèmes locaux sont différents. Cette définition assez vague fait toujours l’objet de débats (Moreno et Rodríguez 2010).

Enfin, la diversité \(\gamma\) est similaire à la diversité \(\alpha\), prise en compte sur l’ensemble du système étudié. Les diversités \(\alpha\) et \(\gamma\) se mesurent donc de la même façon.

1.2.2 Décomposition

Whittaker (1977) a proposé sans succès une normalisation des échelles d’évaluation de la biodiversité, en introduisant la diversité régionale \(\varepsilon\) (\(\gamma\) étant réservé au paysage et \(\alpha\) à l’habitat) et la diversité \(\delta\) entre les paysages. Seuls les trois niveaux originaux ont été conservés par la littérature, sans définition stricte des échelles d’observation.

La distinction entre les diversités \(\alpha\) et \(\beta\) dépend de la finesse de la définition de l’habitat. La distinction de nombreux habitats diminue la diversité \(\alpha\) au profit de la \(\beta\). Il est donc important de définir une mesure qui ne dépende pas de ce découpage, donc une mesure cumulative (additive ou multiplicative) décrivant la diversité totale, décomposable en la somme ou le produit convenablement pondérés de toutes les diversités \(\alpha\) des habitats (diversité intra) et de la diversité \(\beta\) inter-habitat.

Nous appellerons communauté le niveau de découpage concernant la diversité \(\alpha\) et méta-communauté le niveau de regroupement pour l’estimation de la diversité \(\gamma\).

1.3 Le problème de l’espèce

Évaluer la richesse spécifique suppose que les espèces soient définies clairement, ce qui n’est de toute évidence pas le cas (Casetta 2014). Le premier aspect du problème concerne la nature des espèces : réalité naturelle ou seulement représentation simplificatrice. Une analyse historique et philosophique en est faite par Richards (2010). L’autre aspect, avec des conséquences pratiques plus immédiates, concerne leur délimitation. Mayden (1997) recense vingt-deux définitions différentes du concept d’espèce. Wilkins (2011) estime qu’il n’y a qu’un seul concept d’espèce mais sept définitions, c’est-à-dire sept façons de les identifier, et vingt-sept variations ou mélanges de ces définitions.

La définition historique est celle de morphoespèce, qui classe les espèces selon leurs formes, supposées d’abord immuables. La définition moderne la plus répandue est celle d’espèce biologique (Dobzhansky 1937) : un “groupe de populations naturelles isolées reproductivement les unes des autres” (Mayr 1942). Lorsque les populations d’une espèce sont isolées géographiquement, leur capacité à se reproduire ensemble est toute théorique (et rarement vérifiée expérimentalement). Des populations allopatriques n’ont pas de flux de gènes réels entre elles et peuvent être considérées comme des espèces distinctes selon la définition d’espèce phylogénétique : “le plus petit groupe identifiable d’individus avec un pattern commun d’ancêtres et de descendants” (Cracraft 1983). C’est l’unité génétique détectée par la méthode du coalescent pour la délimitation des espèces (Sukumaran et Knowles 2017). Le nombre d’espèces phylogénétiques est bien supérieur au nombre d’espèces biologiques. Enfin, Van Valen (1976) définit les espèces par la niche écologique qu’elles occupent (à partir de l’exemple des chênes blancs européens) plutôt que par les flux de gènes (permanents entre les espèces distinctes) : la définition écologique d’espèce est proche du concept de complexe d’espèces (ensemble d’espèces voisines échangeant des gènes, Pernès 1984).

Le choix de la définition modifie considérablement sur la quantification de la richesse (Agapow et al. 2004). Des problèmes méthodologiques s’ajoutent aux problèmes conceptuels (Hey 2001) : la séparation ou le regroupement de plusieurs populations ou morphotypes en un nombre plus ou moins grand d’espèces est un choix qui reflète les connaissances du moment et peut évoluer (Barberousse et Samadi 2014).

L’impact du problème de l’espèce sur la mesure de la diversité reste sans solution à ce stade, si ce n’est d’utiliser les mêmes définitions si des communautés différentes doivent être comparées. L’approche phylogénétique (chapitre 8) permet de contourner le problème : si deux taxons très semblables apportent à peine plus de diversité qu’un seul taxon, le choix de les distinguer ou non n’est pas critique.