13 Décomposition de la diversité phylogénétique et fonctionnelle

L’entropie phylogénétique et l’entropie de Ricotta et Szeidl se décomposent comme l’entropie HCDT. La diversité $\beta$ phylogénétique et la diversité $\beta$ de Leinster et Cobbold sont des nombres effectifs de communautés, c’est-à-dire des communautés de même poids et dont les espèces seraient totalement dissimilaires qui fourniraient la même entropie $\beta$ que les communautés réelles.

L’entropie phylogénétique est une combinaison linéaire de l’entropie HCDT donc sa décomposition est identique (Marcon et Hérault 2015a).

13.1 Décomposition de la diversité phylogénétique

En combinant l’équation (8.1) et le tableau 12.3, on obtient

\[\begin{equation} \tag{13.1} ^{q}\!\bar{H}_{\gamma}\left(T\right) = ^{q}\!\bar{H}_{\alpha}\left(T\right) + ^{q}\!\bar{H}_{\beta}\left(T\right). \end{equation}\]

L’entropie $\gamma$ est celle de la méta-communauté, l’entropie $\alpha$ est la somme pondérée de celles des communautés, la pondération est libre mais doit respecter $p_s=\sum_i{w_ip_{s|i}}$ :

\[\begin{equation} \tag{13.2} ^{q}\!\bar{H}_{\alpha}\left(T\right) = \sum_i{w_i{^{q}_{i}\!\bar{H}_{\alpha}}\left(T\right)}. \end{equation}\]

L’entropie $\beta$ est

\[\begin{align} \tag{13.3} ^{q}\!\bar{H}_{\beta}\left(T\right) &= \sum_i{w_i}^{q}_{i}\!\bar{H}_{\beta}\left(T\right)\\ &= \sum_i{w_i}\sum_k{\frac{T_k}{T}^{q}_{ik}\!H_{\beta}}\\ &= \sum_i{w_i}\sum_k{\frac{T_k}{T}\sum_u{p^{q}_{k,u,i}\ln_q\frac{p_{k,u,i}}{p_{k,u}}}} \end{align}\]

où $p_{k,u}$ est la probabilité d’observer une des espèces de la branche $u$ de l’arbre à la période $k$ (figure 7.7) dans la méta-communauté, et $p_{k,u,i}$ la même probabilité dans la communauté $i$.

La décomposition de l’entropie phylogénétique au sens de Allen, Kon, et Bar-Yam (2009), c’est-à-dire dans la cas particulier $q=1$, a été établie par Mouchet et Mouillot (2011).

La fonction DivPart de entropart permet de décomposer l’entropie. Les résultats contiennent la valeur de la diversité :

data(Paracou618)
summary(DivPart(q = 1, Paracou618.MC, Biased = FALSE,
                Tree = Paracou618.Taxonomy))

## HCDT diversity partitioning of order 1 of metaCommunity 
## Paracou618.MC
##  with correction: UnveilJ UnveilJ UnveilJ
## Phylogenetic or functional diversity was calculated
## according to the tree 
## Paracou618.Taxonomy 
## 
## Diversity is normalized 
## 
## Alpha diversity of communities: 
##     P006     P018 
## 37.42057 53.73643 
## Total alpha diversity of the communities: 
## [1] 43.6882
## Beta diversity of the communities: 
## [1] 1.273686
## Gamma diversity of the metacommunity: 
## [1] 55.64502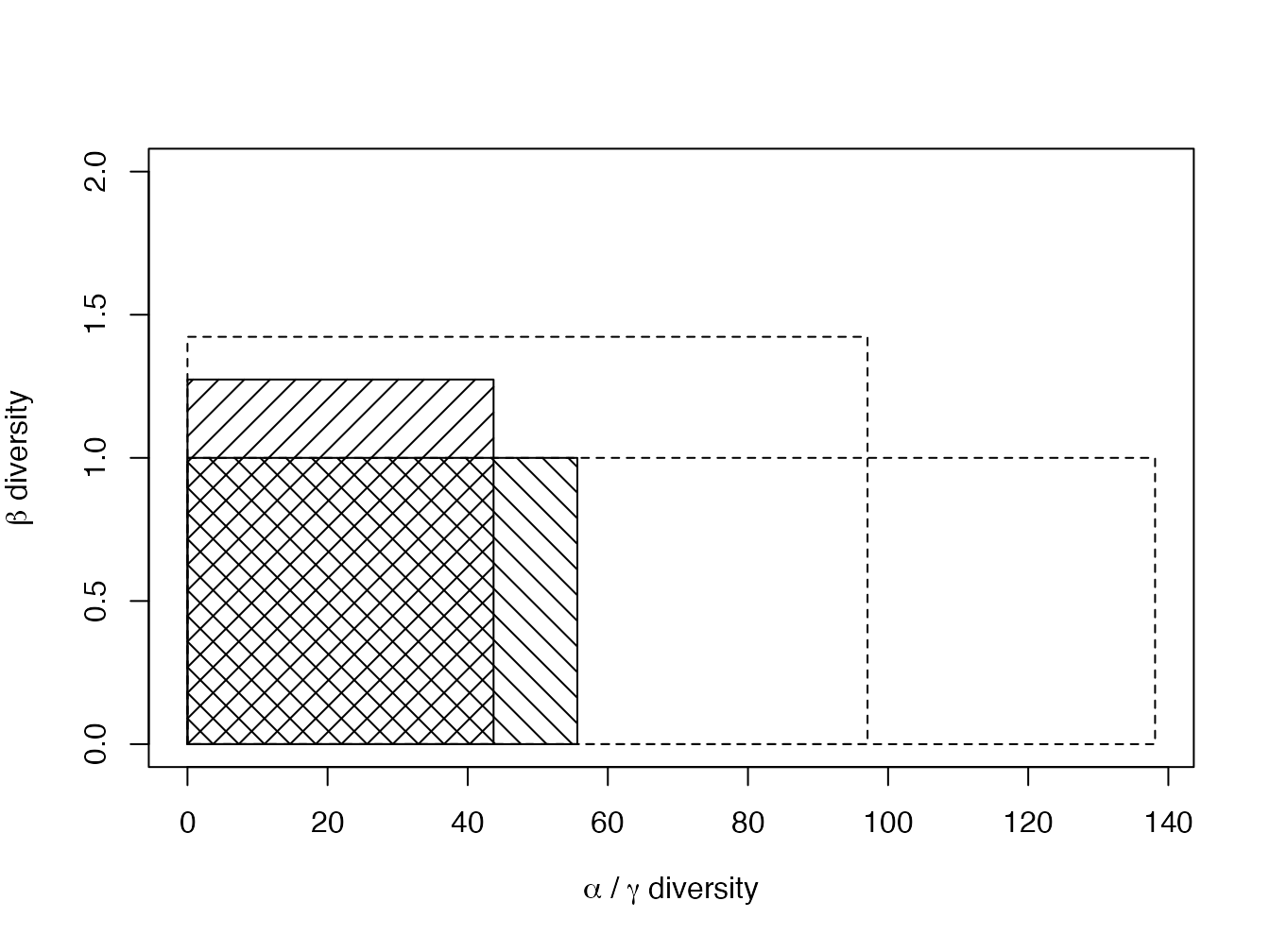

$Représentation graphique de la diversité des deux parcelles du jeu de données Paracou618. Les rectangles transparents représentent la diversité neutre, les rectangles hachurés la diversité phylogénétique (l’arbre est la taxonomie des espèces, $q=1$). Dans chaque cas, le rectangle le plus large, de hauteur 1, représente la diversité $\\gamma$. Le rectangle plus haut a pour largeur et longueur les diversités $\alpha$ et $\beta$. Les surfaces des deux rectangles sont identiques.$

Figure 13.1: Représentation graphique de la diversité des deux parcelles du jeu de données Paracou618. Les rectangles transparents représentent la diversité neutre, les rectangles hachurés la diversité phylogénétique (l’arbre est la taxonomie des espèces, $q=1$). Dans chaque cas, le rectangle le plus large, de hauteur 1, représente la diversité $\\gamma$. Le rectangle plus haut a pour largeur et longueur les diversités $\alpha$ et $\beta$. Les surfaces des deux rectangles sont identiques.

La figure 13.1 donne une représentation graphique de la décomposition de la diversité. La différence de taille entre les rectangles hachurés et les rectangles transparents est due à la prise en compte de la phylogénie. La diversité $\gamma$ (rectangles de hauteur 1) est égale au produit des diversités $\alpha$ et $\beta$ (côtés du rectangle plus haut). Si les communautés étaient de même poids et complètement différentes, c’est à dire contenant des espèces totalement dissimilaires entre communautés (Pavoine, Marcon, et Ricotta 2016), la hauteur du rectangle serait égale à leur nombre (2 ici).

Code pour réaliser la figure :

q <- 1
Neutre <- DivPart(q, Paracou618.MC, Biased = FALSE)
plot(c(0, Neutre$GammaDiversity), c(0, Paracou618.MC$Ncommunities),
     type = "n", 
     xlab = expression(paste(alpha, " / ", gamma, " diversity")), 
     ylab = expression(paste(beta, " diversity")))
rect(0, 0, Neutre$GammaDiversity, 1, lty=2)
rect(0, 0, Neutre$TotalAlphaDiversity, Neutre$TotalBetaDiversity, 
     lty = 2)
Phylo <- DivPart(q, Paracou618.MC, Biased = FALSE, 
                 Tree = Paracou618.Taxonomy)
rect(0, 0, Phylo$GammaDiversity, 1, angle=135, density=10)
rect(0, 0, Phylo$TotalAlphaDiversity, Phylo$TotalBetaDiversity,
     density = 10)

13.2 Partitionnement de la diversité de Leinster et Cobbold

Selon les mêmes principes que pour la décomposition de l’entropie HCDT, Marcon, Zhang, et Hérault (2014) ont décomposé l’entropie de Ricotta et Szeidl (2006). L’entropie $\alpha$ de la communauté $i$ est

\[\begin{equation} \tag{13.4} ^q_i\!H^{\mathbf{Z}}_\alpha = \frac{1-\sum_s{p_{s|i}{\left(\mathbf{Zp}\right)}^{q-1}_{s|i}}}{q-1}. \end{equation}\]

L’entropie $\alpha$ est la somme pondérée des entropies des communautés :

\[\begin{equation} \tag{13.5} ^q\!H^{\mathbf{Z}}_\alpha = \sum_i{w_i \, ^q_i\!H^{\mathbf{Z}}_\alpha} = \frac{1-\sum_i{w_i\sum_s{p_{s|i}{\left(\mathbf{Zp}\right)}^{q-1}_{s|i}}}}{q-1}. \end{equation}\]

L’entropie $\beta$ est similaire à l’entropie $\beta$ HCDT : c’est la divergence généralisée de Jensen-Shannon entre les distributions de $\mathbf{Zp}$ des communautés. Formellement :

\[\begin{equation} \tag{13.6} ^q\!H^{\mathbf{Z}}_\beta =\sum_i{w_i}\sum_{s}{p_{s|i}\left(\ln_q\frac{1}{{\left(\mathbf{Zp}\right)}_s}-\ln_q\frac{1}{{\left(\mathbf{Zp}\right)}_{s|i}}\right)}. \end{equation}\]

La diversité $\beta$ est obtenue en calculant l’exponentielle déformée de la décomposition additive de l’entropie :

\[\begin{equation} \tag{13.7} ^q\!D^{\mathbf{Z}}_\beta =e^{\frac{^qH^{\mathbf{Z}}}{1+\left(1-q\right)\,{^qH^{\mathbf{Z}}_\alpha}}}_q. \end{equation}\]

La décomposition de la diversité peut être faite directement, sans passer par l’entropie.

L’inverse de $^q\!D^{\mathbf{Z}}_\gamma$ est la moyenne généralisée d’ordre $q-1$ de ${\left(\mathbf{Zp}\right)}_s$ :

\[\begin{equation} \tag{13.8} \frac{1}{^q\!D^{\mathbf{Z}}_\gamma} ={\left[\sum_s{p_s{{\left(\mathbf{Zp}\right)}_s}^{q-1}}\right]}^{\frac{1}{q-1}} \end{equation}\]

Partant de $^{q}\!D_{\gamma} = {^{q}\!D_{\alpha}} {^{q}\!D_{\beta}}$ et de la définition de Routledge de la diversité $\alpha$, on obtient

\[\begin{equation} \tag{13.9} ^q\!D^{\mathbf{Z}}_\beta ={\left[\sum_i{w_i}{\left(\frac{1/^q_i\!D^{\mathbf{Z}}_\alpha}{1/^q\!D^{\mathbf{Z}}_\gamma}\right)}^{q-1}\right]}^{\frac{1}{q-1}}. \end{equation}\]

De la même façon que $1/^q\!D^{\mathbf{Z}}_\gamma$ est la banalité moyenne des espèces, $^q\!D^{\mathbf{Z}}_\beta$ est la banalité moyenne normalisée des communautés, où la banalité normalisée de la communauté $i$ est définie comme ${\left(1/^q_i\!D^{\mathbf{Z}}_\alpha\right)}/{\left(1/^q\!D^{\mathbf{Z}}_\gamma\right)}$, c’est-à-dire la banalité moyenne de ses espèces divisée par celle de la méta-communauté.

La fonction DivPart (comme les autres fonctions avancées de entropart) supporte la décomposition de la diversité de Leinster et Cobbold quand une matrice de similarité lui est passée comme argument à la place d’un arbre phylogénétique pour le calcul de la phylodiversité HCDT :

# Matrice de distances fonctionnelles
DistanceMatrix <- as.matrix(Paracou618.dist)
# Transformation en matrice de similarité
Z <- 1 - DistanceMatrix/max(DistanceMatrix)
# Partition de la diversité
summary(DivPart(q = 1, Paracou618.MC, Z = Z, Biased = FALSE))

## Similarity-based diversity partitioning of order 1 
## of metaCommunity Paracou618.MC
##  with correction: Best
## Phylogenetic or functional entropy was calculated
## according to the similarity matrix 
## Z 
## 
## Alpha diversity of communities: 
##     P006     P018 
## 1.483722 1.482119 
## Total alpha diversity of the communities: 
## [1] 1.483036
## Beta diversity of the communities: 
##     Best 
## 1.003403 
## Gamma diversity of the metacommunity: 
##     Best 
## 1.488083

Le partitionnement de la diversité fonctionnelle de la méta-communauté Paracou618.MC selon la matrice de distances des traits fonctionnels montre que la diversité $\beta$ est extrêmement faible entre les deux parcelles.

12 Décomposition de l’entropie HCDT

14 Tests de significativité