18 Décomposition de la diversité jointe
La diversité jointe peut être décomposée en diversité \(\gamma\) (elle-même décomposable en diversités \(\alpha\) et \(\beta\)) et réplication, égale au nombre effectif de répétitions de l’assemblage des communautés nécessaire pour obtenir la diversité jointe réelle.
La décomposition de la diversité jointe (Gregorius 2009, 2010) complète celle de la diversité \(\gamma\) vue dans les parties précédentes. On se place dans le cadre d’un échantillonnage global de la méta-communauté, dans lequel le poids de chaque communauté est égal à la probabilité qu’un individu lui appartienne, et non un choix arbitraire.
18.1 Définitions
La diversité \(\beta\) mesure la divergence entre la distribution moyenne des espèces dans les communautés et leur distribution dans la méta-communauté. Gregorius la qualifie de “diversité de répartition” (apportionment) (Gregorius 2014). L’exemple suivant mesure la diversité \(\beta\) dans une méta-communauté très simple (figure 18.1) :
q <- 2
df1 <- data.frame(Co1 = c(10, 20, 30, 10), Co2 = c(50, 20, 20,
5), row.names = c("S1", "S2", "S3", "S4"))
library("entropart")
MC1 <- MetaCommunity(df1)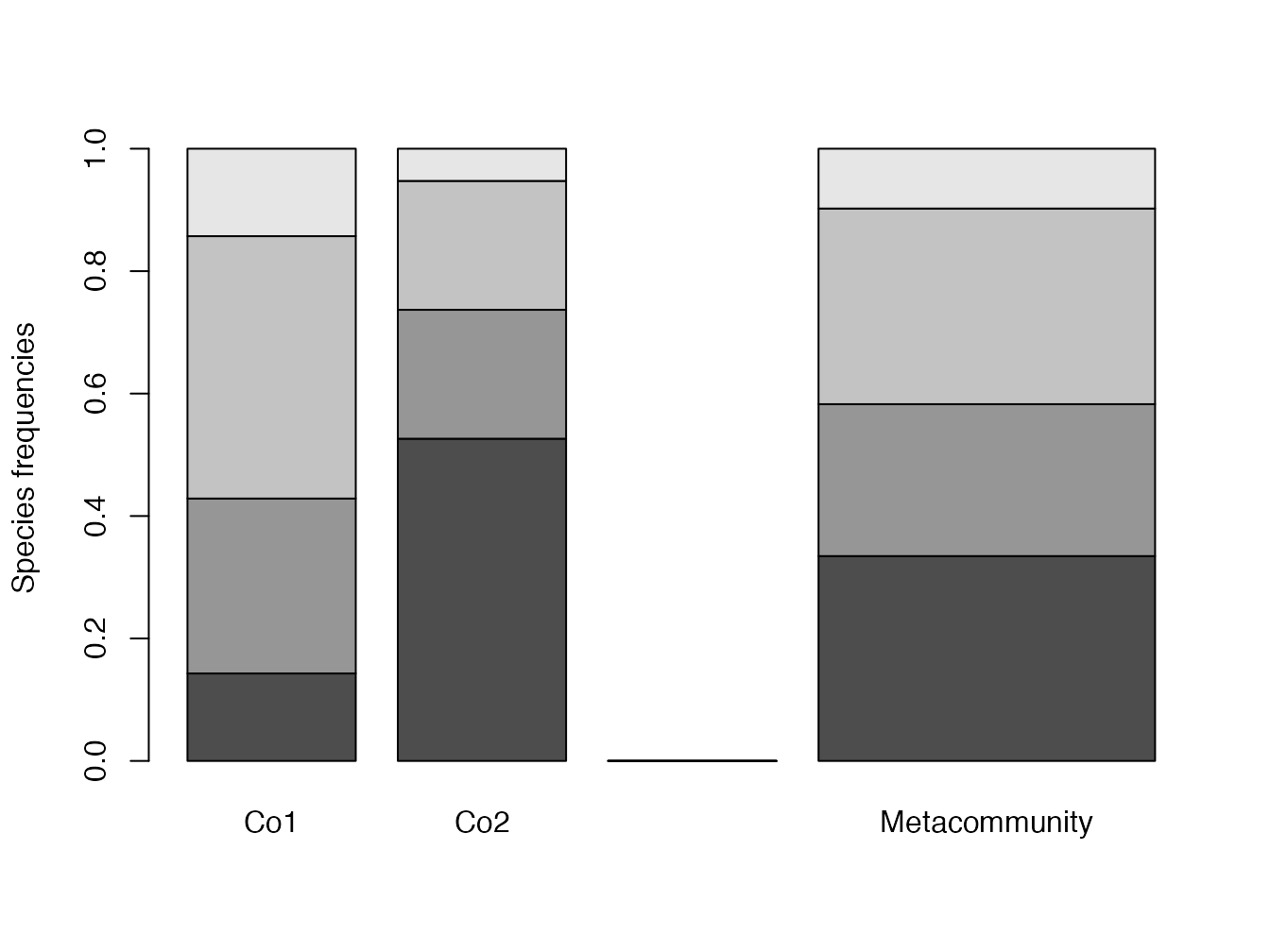
Figure 18.1: Méta-communauté simple.
Le code R nécessaire pour réaliser la figure est :
plot(MC1)## HCDT diversity partitioning of order 2 of metaCommunity MC1
##
## Alpha diversity of communities:
## Co1 Co2
## 3.266667 2.714286
## Total alpha diversity of the communities:
## [1] 2.964968
## Beta diversity of the communities:
## None
## 1.182674
## Gamma diversity of the metacommunity:
## None
## 3.506591Répliquer les communautés à l’identique n’a aucun effet sur la diversité : la diversité \(\alpha\) est la moyenne des diversités des communautés et la diversité \(\gamma\) est celle de leur assemblage dont les proportions ne changent pas. L’exemple suivant concerne une méta-communauté contenant les mêmes communautés, mais en double (figure 18.2) :
df2 <- cbind(df1, df1)
MC2 <- MetaCommunity(df2)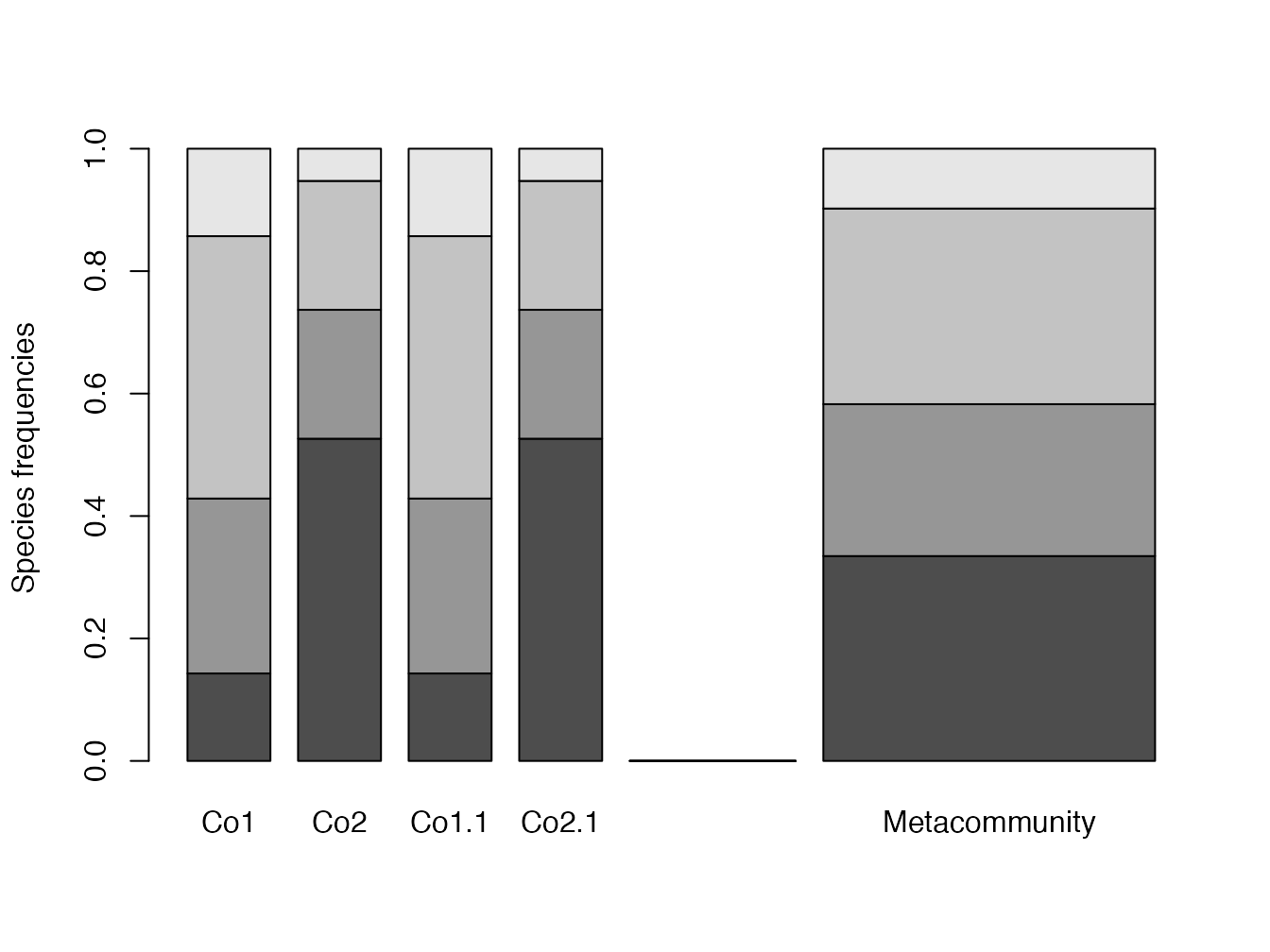
Figure 18.2: Méta-communauté doublant les communautés de la précédente.
Le code R nécessaire pour réaliser la figure est :
plot(MC2)## HCDT diversity partitioning of order 2 of metaCommunity MC2
##
## Alpha diversity of communities:
## Co1 Co2 Co1.1 Co2.1
## 3.266667 2.714286 3.266667 2.714286
## Total alpha diversity of the communities:
## [1] 2.964968
## Beta diversity of the communities:
## None
## 1.182674
## Gamma diversity of the metacommunity:
## None
## 3.506591La diversité jointe \(^{q}\!D_{j}={^{q}\!D}(\{p_{s,i}\})\) est en revanche doublée au cours de l’opération : elle mesure le nombre effectif de catégories (combinaison de l’espèce et de la communauté) du tableau de données :
# Méta-communauté simple
Diversity(as.ProbaVector(df1), q)## None
## 5.642487
# Méta-communauté double
Diversity(as.ProbaVector(df2), q)## None
## 11.28497La distribution de référence pour définir ce nombre effectif correspond à l’équitabilité maximale : \(S\) espèces équiprobables sont réparties dans \(I\) communautés équiprobables. Le nombre effectif est alors \(SI\). Si nombre effectif d’espèces est égal à la diversité \(\gamma\), le rapport entre la diversité jointe et la diversité \(\gamma\), noté \(^{q}\!R_{c}\), est le nombre effectif de méta-communautés identiques produisant la diversité jointe observée. Il mesure la réplication des communautés et complète la diversité \(\gamma\) en fournissant un niveau d’information supplémentaire. Gregorius le qualifie de “diversité de différenciation” (differentiation) parce que \(^{q}\!R_{c}\) compare la distribution réelle à une distribution de référence, et pas seulement les distributions des communautés entre elles. En résumé :
- Le nombre effectif d’espèces \(^{q}_{i}\!D\) de la communauté {i} est le nombre d’espèces équifréquentes nécessaires pour obtenir la diversité observée dans la communauté. La diversité \(\alpha\) est le nombre d’espèces équifréquentes nécessaires dans chaque communauté pour obtenir la diversité observée ;
- La diversité \(\beta\) est le nombre de communautés totalement distinctes (chaque espèce n’est présente que dans une seule communauté), de même poids et de même diversité (cette diversité étant égale à la diversité \(\alpha\)), égal au rapport entre la diversité \(\gamma\) et la diversité \(\alpha\) ;
- La diversité \(\gamma\) est le nombre effectif d’espèces de l’assemblage des communautés ;
- La réplication des communautés est le nombre effectif d’assemblages identiques constituant la méta-communauté.
La décomposition complète de la diversité jointe s’écrit \[\begin{equation} \tag{18.1} ^{q}\!D_{j}= ^{q}\!D_{\alpha} \times ^{q}\!D_{\beta} \times ^{q}\!R_{c}. \end{equation}\]
La méta-communauté suivante illustre cette décomposition : elle contient \(R_c=3\) répliques identiques de \(D_{\beta}=2\) communautés équiprobables totalement distinctes, comprenant chacune \(D_{\alpha}=2\) espèces équiprobables (figure 18.3). Sa diversité jointe est 12 (le nombre de cellules non nulles dans la matrice) :
q <- 2 # Peu importe q
df1 <- data.frame(Co1 = c(10, 10, 0, 0), Co2 = c(0, 0, 10, 10),
row.names = c("S1", "S2", "S3", "S4"))
df3 <- cbind(df1, df1, df1)
MC <- MetaCommunity(df3)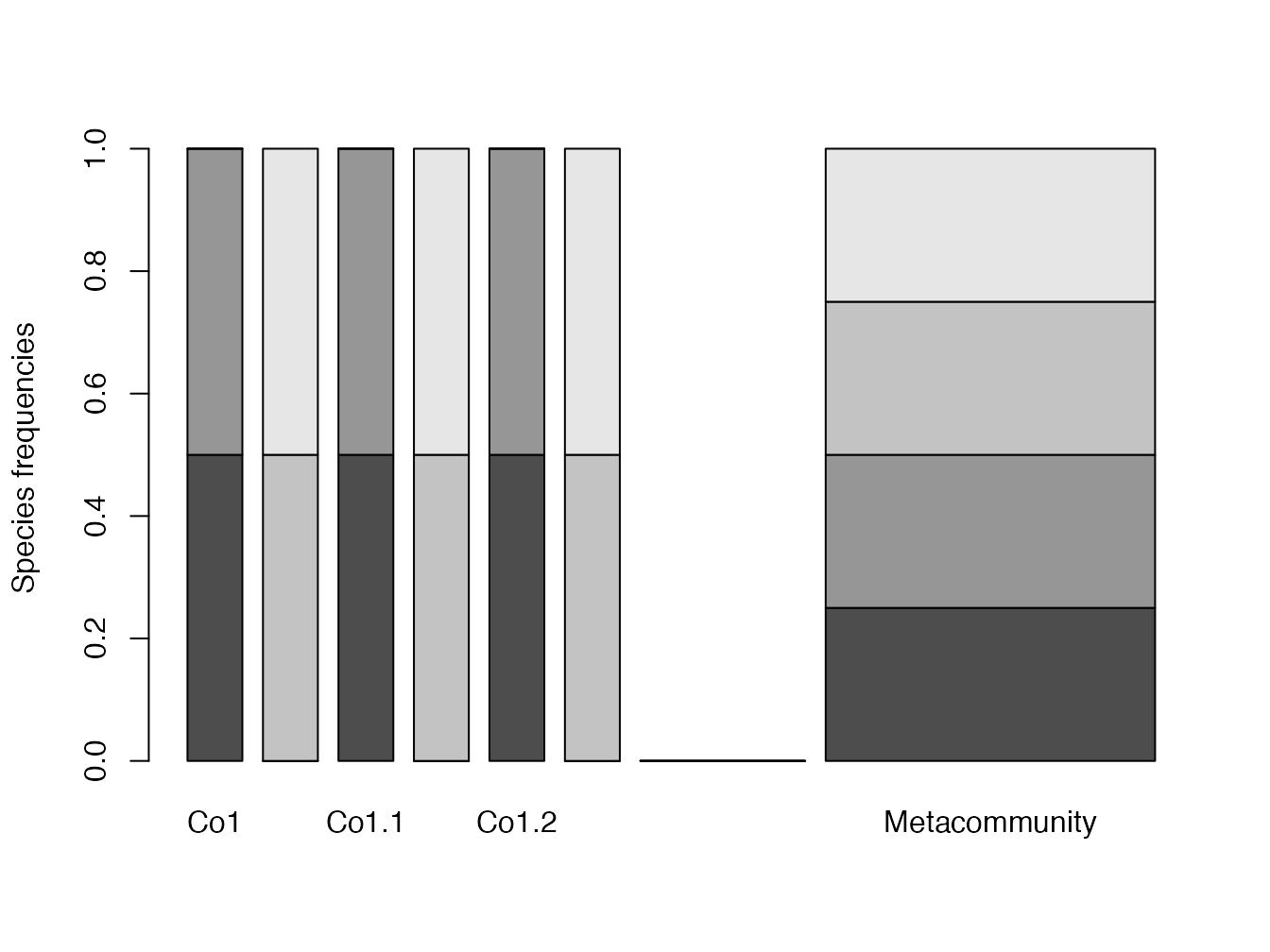
Figure 18.3: Méta-communauté illustrant la décomposition complète de la diversité jointe.
Le code R nécessaire pour réaliser la figure est :
plot(MC)## HCDT diversity partitioning of order 2 of metaCommunity MC
##
## Alpha diversity of communities:
## Co1 Co2 Co1.1 Co2.1 Co1.2 Co2.2
## 2 2 2 2 2 2
## Total alpha diversity of the communities:
## [1] 2
## Beta diversity of the communities:
## None
## 2
## Gamma diversity of the metacommunity:
## None
## 4
(Diversity(as.ProbaVector(df3), q) -> Djointe)## None
## 12
(Dis <- Djointe/dp$GammaDiversity)## None
## 3La définition de la diversité \(\alpha\) de Chiu, Jost, et Chao (2014), équation (10.6), est la diversité jointe, normalisée par le nombre de communautés :
\[\begin{equation} \tag{18.2} ^{q}\!D_{\alpha} = \frac{1}{I} {\left(\sum_s{\sum_i{{\left(w_i p_{s|i}\right)}^q}}\right)}^{{1}/{\left(1-q\right)}} = \frac{1}{I} ^{q}\!D_{j}. \end{equation}\]
18.2 Relations avec d’autres mesures de diversité
En introduisant la définition précédente dans la décomposition de la diversité jointe, équation (18.1), il vient
\[\begin{equation} \tag{18.3} ^{q}\!D_{\beta} = \frac{^{q}\!D_{\gamma}}{^{q}\!D_{\alpha}} = \frac{I}{^{q}\!R_{c}}. \end{equation}\]
La définition de la diversité \(\alpha\) de Chiu et al. implique que la diversité \(\beta\) soit le rapport entre le nombre de communautés et leur réplication. Ce n’est pas une mesure de diversité \(\beta\) de répartition.
En inversant le rôle des lignes et des colonnes de la matrice \(\{p_{s,i}\}\), on peut calculer la réplication des espèces en divisant la diversité jointe par la diversité des poids des communautés :
\[\begin{equation} \tag{18.4} ^{q}\!R_{s} = \frac{^{q}\!D_{j}}{^{q}\!D\left(\{p_{i}\}\right)}. \end{equation}\]
Gregorius montre que \(^{q}\!R_{s}\) égale la diversité \(\alpha\) selon Jost (10.4) :
\[\begin{equation} \tag{18.5} ^{q}\!R_{s} = {\left(\sum_s{\sum_i{\frac{p^q_i}{\sum_i{p^q_i}}p^q_{s|i}}}\right)}^{{1}/{\left(1-q\right)}}. \end{equation}\]