4 Entropie

L’entropie est la surprise moyenne apportée par l’observation des individus d’une communauté, d’autant plus grande qu’un individu appartient à une espèce plus rare. L’entropie HCDT permet d’unifier les indices classiques de diversité : son paramètre, appelé ordre, fixe l’importance donnée aux espèces rares. L’entropie d’ordre 0 est la richesse ; celle d’ordre 1, l’indice de Shannon ; celle d’ordre 2, celui de Simpson. L’entropie est la moyenne du logarithme déformé de la rareté des espèces, définie comme l’inverse de leur probabilité.

L’entropie va de pair avec la diversité au sens strict (Nombres de Hill) : le nombre d’espèces équiprobables dont l’entropie est la même que celle de la communauté réelle. La diversité est l’exponentielle déformée de l’entropie. Les profils de diversité représentent la diversité en fonction de son ordre et permettent la comparaison de communautés.

L’estimation de la diversité est difficile pour des ordres inférieurs à \(0,5\) dans des taxocènes très divers comme les arbres des forêts tropicales.

L’entropie peut être entendue comme la surprise moyenne fournie par l’observation d’un échantillon. C’est intuitivement une bonne mesure de diversité (Pielou 1975). Ses propriétés mathématiques permettent d’unifier les mesures de diversité dans un cadre général.

4.1 Définition de l’entropie

Les textes fondateurs sont Davis (1941) et surtout Theil (1967) en économétrie, et Shannon (1948; 1963) pour la mesure de la diversité. Une revue est fournie par Maasoumi (1993).

Considérons une expérience dont les résultats possibles sont \(\left\{r_1,r_2,\dots ,\ r_S\right\}\). La probabilité d’obtenir \(r_s\) est \(p_s\), et \(\mathbf{p}=(p_1,p_2,\dots,p_S)\) est le vecteur composé des probabilités d’obtenir chaque résultat. Les probabilités sont connues a priori. Tout ce qui suit est vrai aussi pour des valeurs de \(r\) continues, dont on connaîtrait la densité de probabilité.

On considère maintenant un échantillon de valeurs de \(r\). La présence de \(r_s\) dans l’échantillon est peu étonnante si \(p_s\) est grande : elle apporte peu d’information supplémentaire par rapport à la simple connaissance des probabilités. En revanche, si \(p_s\) est petite, la présence de \(r_s\) est surprenante. On définit donc une fonction d’information, \(I(p_s)\), décroissante quand la probabilité augmente, de \(I(0)>0\) (éventuellement \(+\infty\)) à \(I(1)=0\). Chaque valeur observée dans l’échantillon apporte une certaine quantité d’information, dont la somme est l’information de l’échantillon. Patil et Taillie (1982) appellent l’information “rareté”.

La quantité d’information attendue de l’expérience est \(\sum^S_{s=1}{p_s I(p_s) = H(\mathbf{p})}\). Si on choisit \(I\left(p_s\right)=-\ln\left(p_s\right)\), \(H\left(\mathbf{p}\right)\) est l’indice de Shannon, mais bien d’autres formes de \(I\left(p_s\right)\) sont possibles. \(H\left(\mathbf{p}\right)\) est appelée entropie. C’est une mesure de l’incertitude (de la volatilité) du résultat de l’expérience. Si le résultat est certain (une seule valeur \(p_S\) vaut 1), l’entropie est nulle. L’entropie est maximale quand les résultats sont équiprobables.

Si \(\mathbf{p}\) est la distribution des probabilité des espèces dans une communauté, Patil et Taillie (1982) montrent que :

• Si \(I\left(p_s\right) = (1-p_s)/{p_s}\), alors \(H\left(\mathbf{p}\right)\) est le nombre d’espèces \(S\) moins 1 ;
• Si \(I\left(p_s\right)=-\ln\left(p_s\right)\), alors \(H\left(\mathbf{p}\right)\) est l’indice de Shannon ;
• Si \(I\left(p_s\right)=1-p_s\), alors \(H\left(\mathbf{p}\right)\) est l’indice de Simpson.

Figure 4.1: Fonctions d’information utilisées dans le nombre d’espèces (trait plein), l’indice de Shannon (pointillés longs) et l’indice de Simpson (pointillés). L’information apportée par l’observation d’espèces rares décroît du nombre d’espèces à l’indice de Simpson.

Ces trois fonctions d’information sont représentées en figure 4.1.

Le code R nécessaire pour réaliser la figure est :

I0 <- function(p) (1 - p)/p
I1 <- function(p) -log(p)
I2 <- function(p) 1 - p
ggplot(data.frame(x = c(0, 1)), aes(x)) + stat_function(fun = I0) +
    stat_function(fun = I1, lty = 2) + stat_function(fun = I2,
    lty = 3) + coord_cartesian(ylim = c(0, 10)) + labs(x = "p",
    y = "I(p)")

Figure 4.2: Valeur de \(p_{s}I(p_s)\) dans le nombre d’espèces (trait plein), l’indice de Shannon (pointillés longs) et l’indice de Simpson (pointillés). Les espèces rares contribuent peu, sauf pour le nombre d’espèces.

La contribution de chaque espèce à la valeur totale de l’entropie est représentée figure 4.2.

Code R :

H0 <- function(p) 1 - p
H1 <- function(p) -p * log(p)
H2 <- function(p) p * (1 - p)
ggplot(data.frame(x = c(0.001, 1)), aes(x)) + stat_function(fun = H0) +
    stat_function(fun = H1, lty = 2) + stat_function(fun = H2,
    lty = 3) + labs(x = "p", y = "H(p)")

4.2 Entropie relative

Considérons maintenant les probabilités \(q_s\) formant l’ensemble \(\mathbf{q}\) obtenues par la réalisation de l’expérience. Elles sont différentes des probabilités \(p_s\), par exemple parce que l’expérience ne s’est pas déroulée exactement comme prévu. On définit le gain d’information \(I(q_s,p_s)\) comme la quantité d’information supplémentaire fournie par l’observation d’un résultat de l’expérience, connaissant les probabilités a priori. La quantité totale d’information fournie par l’expérience, \(\sum^S_{s=1}{q_sI(q_s,p_s)}=H(\mathbf{q},\mathbf{p})\), est souvent appelée entropie relative. Elle peut être vue comme une distance entre la distribution a priori et la distribution a posteriori. Il est possible que les distributions \(\mathbf{p}\) et \(\mathbf{q}\) soit identiques, que le gain d’information soit donc nul, mais les estimateurs empiriques n’étant pas exactement égaux entre eux, des tests de significativité de la valeur de \(\hat{H}(\mathbf{q},\mathbf{p})\) seront nécessaires.

Quelques formes possibles de \(H(\mathbf{q},\mathbf{p})\) sont :

• La divergence de Kullback-Leibler (Kullback et Leibler 1951) connue par les économistes comme l’indice de dissimilarité de Theil (1967) : \[\begin{equation} \tag{4.1} T = \sum^S_{s=1}{q_{s}\ln\frac{q_s}{p_s}}; \end{equation}\]
• Sa proche parente, appelée parfois deuxième mesure de Theil (Conceição et Ferreira 2000), qui inverse simplement les rôles de \(p\) et \(q\) : \[\begin{equation} \tag{4.2} L = \sum^S_{s=1}{p_{s}\ln\frac{p_s}{q_s}}. \end{equation}\]

Figure 4.3: Valeur de \(q\ln(q/p)\) en fonction de \(p\) et \(q\). La divergence de Kullback-Leibler est la somme de cette valeur pour toutes les espèces

L’entropie relative est essentielle pour la définition de la diversité \(\beta\) présentée dans le chapitre 12. En se limitant à la diversité \(\alpha\), on peut remarquer que l’indice de Shannon est la divergence de Kullback-Leibler entre la distribution observée et l’équiprobabilité des espèces (Marcon et al. 2012). Les valeurs de chaque terme de la divergence sont représentées en figure 4.3.

Le code R nécessaire pour réaliser la figure est :

p <- q <- seq(0.01, 1, 0.01)
KB <- function(p, q) p * log(p/q)
xyz <- t(outer(p, q, FUN = "KB"))
library("sp")
image(xyz, col = bpy.colors(n = 100, cutoff.tails = 0.3, alpha = 0.6),
    xlab = "q", ylab = "p", asp = 1)
contour(xyz, levels = c(seq(-0.3, 0, 0.1), c(0.2, 0.5), seq(1,
    4, 1)), labcex = 1, add = T)

4.3 L’appropriation de l’entropie par la biodiversité

MacArthur (1955) est le premier à avoir introduit la théorie de l’information en écologie (Ulanowicz 2001). MacArthur s’intéressait aux réseaux trophiques et cherchait à mesurer leur stabilité : l’indice de Shannon qui comptabilise le nombre de relations possibles lui paraissait une bonne façon de l’évaluer. Mais l’efficacité implique la spécialisation, ignorée dans \(H\) qui est une mesure neutre (toutes les espèces y jouent le même rôle). MacArthur a abandonné cette voie.

Les premiers travaux consistant à généraliser l’indice de Shannon sont dus à Rényi (1961). L’entropie d’ordre \(q\) de Rényi est

\[\begin{equation} ^{q}\!R =\frac{1}{1-q\ln\sum^S_{q=1}{p^q_s}}. \end{equation}\]

Rényi pose également les axiomes pour une mesure d’entropie \(R\left(\mathbf{p}\right)\), où \(\mathbf{p}=(p_1,p_2,\dots,p_S)\) :

• La symétrie : les espèces doivent être interchangeables, aucune n’a de rôle particulier et leur ordre est indifférent ;
• La mesure doit être continue par rapport aux probabilités ;
• La valeur maximale est atteinte si toutes les probabilités sont égales.

Il montre que \(^{q}\!R\) respecte les 3 axiomes.

Patil et Taillie (1982) ont montré de plus que :

• L’introduction d’une espèce dans une communauté augmente sa diversité (conséquence de la décroissance de \(g(p_s)\)) ;
• Le remplacement d’un individu d’une espèce fréquente par un individu d’une espèce plus rare augmente l’entropie à condition que \(R(\mathbf{p})\) soit concave. Dans la littérature économique sur les inégalités, cette propriété est connue sous le nom de Pigou-Dalton (Dalton 1920).

Hill (1973) transforme l’entropie de Rényi en nombres de Hill, qui en sont simplement l’exponentielle :

\[\begin{equation} \tag{4.3} ^{q}\!D = {\left(\sum^S_{s=1}{p^q_s}\right)}^{\frac{1}{1-q}}. \end{equation}\]

Le souci de Hill était de rendre les indices de diversité intelligibles après l’article remarqué de Hurlbert (1971) intitulé “le non-concept de diversité spécifique”. Hurlbert reprochait à la littérature sur la diversité sa trop grande abstraction et son éloignement des réalités biologiques, notamment en fournissant des exemples dans lesquels l’ordre des communautés n’est pas le même selon l’indice de diversité choisi. Les nombres de Hill sont le nombre d’espèces équiprobables donnant la même valeur de diversité que la distribution observée. Ils sont des transformations simples des indices classiques :

• \(^{0}\!D\) est le nombre d’espèces ;
• \(^{1}\!D=e^H\), l’exponentielle de l’indice de Shannon ;
• \(^{2}\!D={1}/{\left(1-E\right)}\), l’inverse de l’indice de concentration de Simpson, connu sous le nom d’indice de Stoddart (1983).

Ces résultats avaient déjà été obtenus avec une autre approche par MacArthur (1965) et repris par Adelman (1969) dans la littérature économique.

Les nombres de Hill sont des “nombres effectifs” ou “nombres équivalents”. Le concept a été défini rigoureusement par Gregorius (1991), d’après S. Wright (1931) (qui avait le premier défini la taille effective d’une population) : étant donné une variable caractéristique (ici, l’entropie) fonction seulement d’une variable numérique (ici, le nombre d’espèces) dans un cas idéal (ici, l’équiprobabilité des espèces), le nombre effectif est la valeur de la variable numérique pour laquelle la variable caractéristique est celle du jeu de données.

Gregorius (2014) montre que de nombreux autres indices de diversité sont acceptables dans le sens où ils vérifient les axiomes précédents et, de plus, que la diversité d’un assemblage de communautés est obligatoirement supérieure à la diversité moyenne de ces communautés (l’égalité n’étant possible que si les communautés sont toutes identiques). Cette dernière propriété sera traitée en détail dans la partie consacrée à la décomposition de la diversité. Ces indices doivent vérifier deux propriétés : leur fonction d’information doit être décroissante, et ils doivent être une fonction strictement concave de \(p_s\). Parmi les possibilités, \(I(p_s) = \cos{(p_s {\pi}/{2})}\) est envisageable par exemple : le choix de la fonction d’information est virtuellement illimité, mais seules quelques unes seront interprétables clairement.

Un nombre équivalent d’espèces existe pour tous ces indices, il est toujours égal à l’inverse de l’image de l’indice par la réciproque de la fonction d’information :

\[\begin{equation} \tag{4.4} D = \frac{1}{I^{-1}\left(\sum^S_{s=1}{p_s I(p_s)}\right)}. \end{equation}\]

D’autres entropies ont été utlisées, avec plus ou moins de succès. Par exemple, Ricotta et Avena (2003b) proposent d’utiliser la fonction d’information \(I(p_s)=-\ln(k_s)\) où \(k_s\) est la dissimilarité totale de l’espèce \(s\) avec les autres (par exemple, la somme des distances aux autres espèces dans un arbre phylogénétique, voir section 6.2), normalisée pour que \(\sum_s{k_s}=1\). Ainsi, les espèces les plus originales apportent peu d’information, ce qui n’est pas très intuitif. Les auteurs montrent que leur mesure est la somme de l’entropie de Shannon et de la divergence de Kullback-Leibler entre les probabilités et les dissimilarités des espèces. Ricotta et Szeidl (2006) ont défini plus tard une entropie augmentant avec l’originalité de chaque espèce, présentée au chapitre 9.

4.4 Entropie HCDT

Tsallis (1988) propose une classe de mesures appelée entropie généralisée, définie par Havrda et Charvát (1967) pour la première fois et redécouverte plusieurs fois, notamment par Daróczy (1970), d’où son nom entropie HCDT (voir Mendes et al. (2008), page 451, pour un historique complet) :

\[\begin{equation} \tag{4.5} ^{q}\!H = \frac{1}{q-1}\left(1-\sum^S_{s=1}{p^q_s}\right). \end{equation}\]

Tsallis a montré que les indices de Simpson et de Shannon étaient des cas particuliers d’entropie généralisée, retrouvant, sans faire le rapprochement (Ricotta 2005c), la définition d’un indice de diversité de Patil et Taillie (1982).

Ces résultats ont été complétés par d’autres et repris en écologie par Keylock (2005) et Jost (2006, 2007). Là encore :

• Le nombre d’espèces moins 1 est \(^{0}\!H\) ;
• L’indice de Shannon est \(^{1}\!H\) ;
• L’indice de Gini-Simpson est \(^{2}\!H\).

L’entropie HCDT est particulièrement attractive parce que sa relation avec la diversité au sens strict est simple, après introduction du formalisme adapté (les logarithmes déformés). Son biais d’estimation peut être corrigé globalement, et non seulement pour les cas particuliers (nombre d’espèces, Shannon, Simpson). Enfin, sa décomposition sera présentée en détail dans le chapitre 12.

4.4.1 Logarithmes déformés

L’écriture de l’entropie HCDT est largement simplifiée en introduisant le formalisme des logarithmes déformés (Tsallis 1994). Le logarithme d’ordre \(q\) est défini par \[\begin{equation} \tag{4.6} \ln_q{x} = \frac{x^{1-q}-1}{1-q}, \end{equation}\] dont la forme est identique à la transformation de Box et Cox (1964) utilisée en statistiques pour normaliser une variable.

Le logarithme déformé converge vers le logarithme naturel quand \(q\to 1\) (figure 4.4).

Le code R nécessaire pour réaliser la figure est :

ln0 <- function(p) lnq(p, 0)
ln2 <- function(p) lnq(p, 2)
lnm1 <- function(p) lnq(p, -1)
ggplot(data.frame(x = c(0, 1)), aes(x)) + 
    stat_function(fun = log) +
    stat_function(fun = ln0, lty = 2, col = "red") +
    stat_function(fun = ln2, lty = 3, col = "blue") +
    stat_function(fun = lnm1, lty = 4, col = "green") +
    coord_cartesian(ylim = c(-4, 0)) +
    labs(x = "p", y = expression(ln[q](p)))

Sa fonction inverse est l’exponentielle d’ordre \(q\) :

\[\begin{equation} \tag{4.7} e^x_q = \left[ 1+\left( 1-q \right)x \right]^{\frac{1}{1-q}}. \end{equation}\]

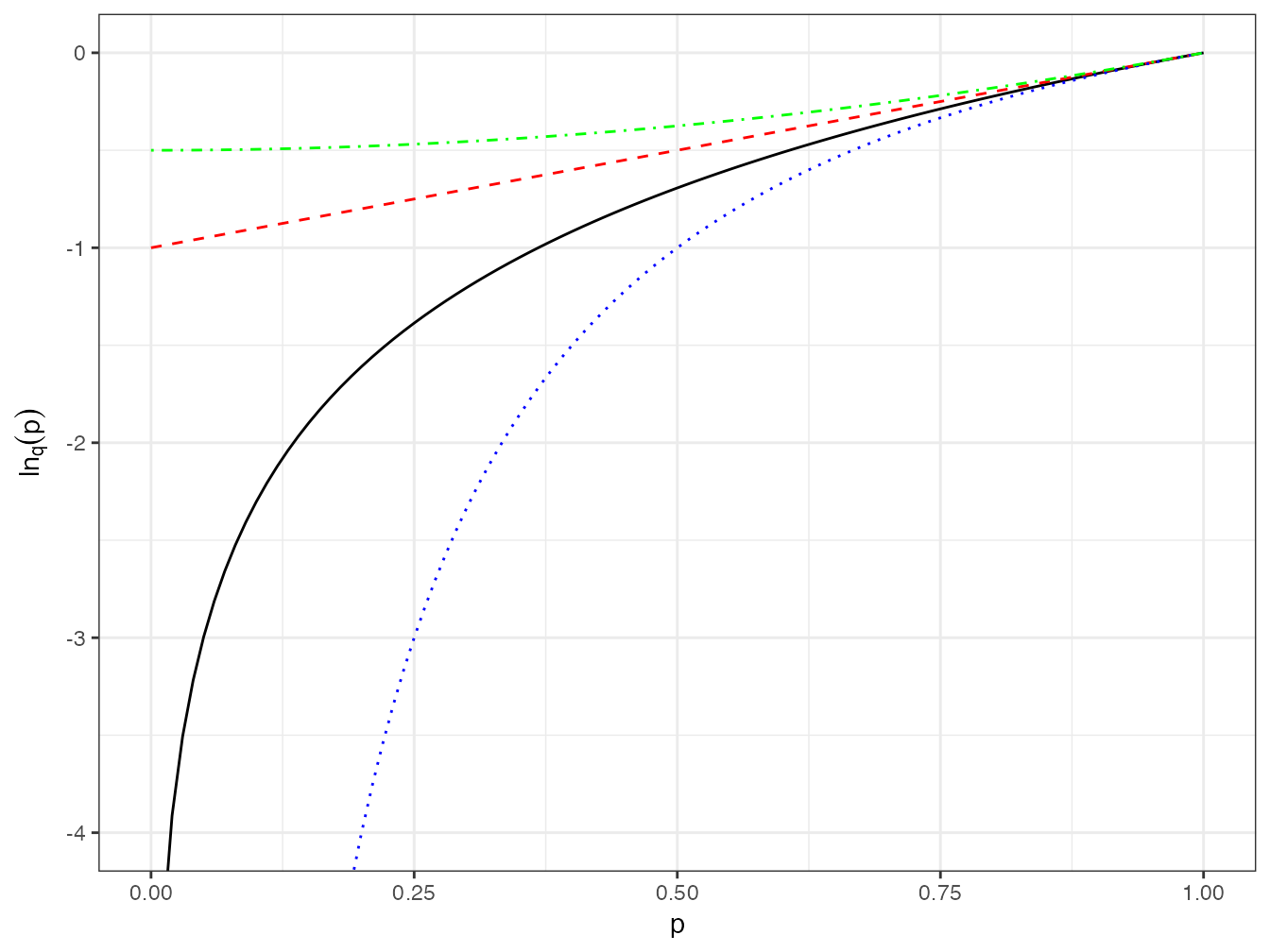
Figure 4.4: Valeur du logarithme d’ordre \(q\) de probabilités entre 0 et 1 pour différentes valeurs de \(q\) : \(q = 0\) (pointillés longs rouges), la courbe est une droite ; \(q = 1\) (trait plein) : logarithme naturel ; \(q = 2\) (pointillés courts bleus) : la courbe a la même forme que le logarithme naturel pour les valeurs positives de \(q\) ; \(q =-1\) (pointillés alternés verts) : la courbe est convexe pour les valeurs négatives de \(q\).

Enfin, le logarithme déformé est subadditif :

\[\begin{equation} \tag{4.8} \ln_q\left(xy\right)=\ln_q{x}+\ln_q{y}-\left(q-1\right)\left(\ln_q{x}\right)\left(\ln_q{y}\right). \end{equation}\]

Ses propriétés sont les suivantes :

\[\begin{equation} \tag{4.9} \ln_q\frac{1}{x}=-x^{q-1}\ln_qx; \end{equation}\]

\[\begin{equation} \tag{4.10} \ln_q\left(xy\right)=\ln_q{x}+x^{1-q}\ln_q{y}; \end{equation}\]

\[\begin{equation} \tag{4.11} \ln_q\left(\frac{x}{y}\right)=\ln_q{x}-{\left(\frac{x}{y}\right)}^{1-q}\ln_q{y}; \end{equation}\]

et

\[\begin{equation} \tag{4.12} e^{x+y}_q = e_q^x e^{\frac{y}{1+\left(1-q\right)x}}_q. \end{equation}\]

Si \(q>1\), \({\mathop{\lim}_{x\to +\infty} \left(\ln_q{x}\right)={1}/{\left(q-1\right)}}\), donc \(e^x_q\) n’est pas définie pour \(x>{1}/{\left(q-1\right)}\).

La dérivée du logarithme déformé est, quel que soit \(q\), \[\begin{equation} \tag{4.13} \ln'_q\left(x\right) = x^{-q}. \end{equation}\]

Les dérivées première et seconde de l’exponentielle déformée sont, quel que soit \(q\) : \[\begin{equation} \tag{4.14} \exp'_q\left(x\right) = \left( e_q^x \right)^{q}; \end{equation}\] \[\begin{equation} \tag{4.15} \exp''_q\left(x\right) = \left( e_q^x \right)^{2q-1}. \end{equation}\]

Ces fonctions sont implémentées dans le package entropart : lnq(x, q) et expq(x, q).

L’entropie d’ordre \(q\) s’écrit

\[\begin{equation} \tag{4.16} ^{q}\!H = \frac{1}{q-1}\left(1-\sum^S_{s=1}{p^q_s}\right)=-\sum_s{p^q_s}\ln_q{p_s}=\sum_s{p_s}\ln_q\frac{1}{p_s}. \end{equation}\]

Ces trois formes sont équivalentes mais les deux dernières s’interprètent comme une généralisation de l’entropie de Shannon (Marcon et al. 2014).

Le calcul de \(^{q}\!H\) peut se faire avec la fonction Tsallis de la librairie entropart :

Ps <- as.ProbaVector(colSums(BCI))
q <- 1.5
Tsallis(Ps, q)

##     None 
## 1.715954

4.4.2 Entropie et diversité

On voit immédiatement que l’entropie de Tsallis est le logarithme d’ordre \(q\) du nombre de Hill correspondant, comme l’entropie de Rényi en est le logarithme naturel :

\[\begin{equation} \tag{4.17} ^{q}\!H = \ln_q{^{q}\!D}; \end{equation}\]

\[\begin{equation} \tag{4.18} ^{q}\!D = e_q^{^{q}\!H}. \end{equation}\]

L’entropie est utile pour les calculs : la correction des biais d’estimation notamment. Les nombres de Hill, ou nombres équivalents d’espèces ou nombres effectif d’espèces permettent une appréhension plus intuitive de la notion de biodiversité (Jost 2006). En raison de leurs propriétés, notamment de décomposition (voir le chapitre 12), Jost (2007) les appelle “vraie diversité”. Hoffmann et Hoffmann (2008) critiquent cette définition totalitaire et fournissent une revue historique plus lointaine sur les origines de ces mesures. Jost (2009b) reconnaît qu’un autre terme aurait pu être choisi (“diversité neutre” ou “diversité mathématique” par exemple).

Dauby et Hardy (2012) écrivent “diversité au sens strict” ; Gregorius (2010) “diversité explicite”.

Quoi qu’il en soit, les nombres de Hill respectent le principe de réplication (voir Chao, Chiu, et Jost (2010), section 3 pour une discussion et un historique) : si \(I\) communautés de même taille, de même niveau de diversité \(D\), mais sans espèces en commun sont regroupées dans une méta-communauté, la diversité de la méta-communauté doit être \(I\times D\).

L’intérêt de ces approches est de fournir une définition paramétrique de la diversité, qui donne plus ou moins d’importance aux espèces rares :

• \(^{-\infty}\!D={1}/{\min(p_S)}\) est l’inverse de la proportion de la communauté représentée par l’espèce la plus rare (toutes les autres espèces sont ignorées). Le biais d’estimation est incontrôlable : l’espèce la plus rare n’est pas dans l’échantillon tant que l’inventaire n’est pas exhaustif ;
• \(^{0}\!D\) est le nombre d’espèces (alors que \(^{0}\!H\) est le nombre d’espèces moins 1). C’est la mesure classique qui donne le plus d’importance aux espèces rares : toutes les espèces ont la même importance, quel que soit leur effectif en termes d’individus. Il est bien adapté à une approche patrimoniale, celle du collectionneur qui considère que l’existence d’une espèce supplémentaire a un intérêt en soi, par exemple parce qu’elle peut contenir une molécule valorisable. Comme les espèces rares sont difficiles à échantillonner, le biais d’estimation est très important, et sa résolution a généré une littérature en soi ;
• \(^{1}\!D\) est l’exponentielle de l’indice de Shannon donne la même importance à tous les individus. Il est adapté à une approche d’écologue, intéressé par les interactions possibles : le nombre de combinaisons d’espèces en est une approche satisfaisante. Le biais d’estimation est sensible ;
• \(^{2}\!D\) est l’inverse de l’indice de concentration de Gini-Simpson donne moins d’importance aux espèces rares. Hill (1973) l’appelle “le nombre d’espèces très abondantes”. Il comptabilise les interactions possibles entre paires d’individus : les espèces rares interviennent dans peu de paires, et influent peu sur l’indice. En conséquence, le biais d’estimation est très petit ; de plus, un estimateur non biaisé existe ;
• \(^{\infty}\!D={1}/{d}\) est l’inverse de l’indice de Berger-Parker (Berger et Parker 1970) qui est la proportion de la communauté représentée par l’espèce la plus abondante : \(d=\max(\mathbf{p})\). Toutes les autres espèces sont ignorées.

Le calcul de \(^{q}\!D\) peut se faire avec la fonction Diversity de la librairie entropart :

Ps <- as.ProbaVector(colSums(BCI))
q <- 1.5
Diversity(Ps, q)

##     None 
## 49.57724

Les propriétés mathématiques de la diversité ne sont pas celles de l’entropie. L’entropie doit être une fonction concave des probabilités comme on l’a vu plus haut, mais pas la diversité (un exemple de confusion est fourni par Gadagkar (1989), qui reproche à \(^{2}\!D\) de ne pas être concave). L’entropie est une moyenne pondérée par les probabilités de la fonction d’information, c’est donc une fonction linéaire des probabilités, propriété importante pour définir l’entropie \(\alpha\) (section 10.3.4) comme la moyenne des entropies de plusieurs communautés, ou l’entropie phylogénétique (chapitre 8) comme la moyenne de l’entropie sur les périodes d’un arbre. La diversité n’est pas une fonction linéaire des probabilités : la diversité moyenne n’est en général pas la moyenne des diversités.

4.4.3 Synthèse

L’inverse de la probabilité d’une espèce, \(1/p_s\), définit sa rareté. L’entropie est la moyenne du logarithme de la rareté :

\[\begin{equation} \tag{4.19} ^{q}\!H = \frac{1}{q-1}\left(1-\sum^S_{s=1}{p^q_s}\right)=\sum_s{p_s}\ln_q\frac{1}{p_s}. \end{equation}\]

La diversité est son exponentielle :

\[\begin{equation} \tag{4.20} ^{q}\!D = e_q^{^{q}\!H}. \end{equation}\]

4.5 Profils de diversité

Leinster et Cobbold (2012), après Hill (1973), Patil et Taillie (1982), Tothmeresz (1995) et Kindt, Van Damme, et Simons (2006), recommandent de tracer des profils de diversité, c’est-à-dire la valeur de la diversité \(^{q}\!D\) en fonction de l’ordre \(q\) (figure 4.5) pour comparer plusieurs communautés. Une communauté peut être déclarée plus diverse qu’une autre si son profil de diversité est au-dessus de l’autre pour toutes les valeurs de \(q\). Si les courbes se croisent, il n’y a pas de relation d’ordre (Tothmeresz 1995).

Lande, DeVries, et Walla (2000) montrent que si la diversité de Simpson et la richesse de deux communautés n’ont pas le même ordre, alors les courbes d’accumulation du nombre d’espèces en fonction du nombre d’individus échantillonnés se croisent aussi.

Figure 4.5: Profil de diversité calculé pour deux parcelles de Paracou (Parcelle 6 : trait plein et Parcelle 18 : trait pointillé). La correction du biais d’estimation est celle de Chao et Jost.

Code R pour réaliser la figure 4.5 :

q.seq <- seq(0, 2, .1)
  P6D<- CommunityProfile(Diversity, Paracou618.MC$Nsi[, 1], q.seq)
  P18D<- CommunityProfile(Diversity, Paracou618.MC$Nsi[, 2], q.seq)
  autoplot(P6D, xlab = "q", ylab = "Diversité") +
    geom_line(aes(x, y), as.data.frame.list(P18D), lty = 2)

Pallmann et al. (2012) ont développé un test statistique pour comparer la diversité de deux communautés pour plusieurs valeurs de \(q\) simultanément.

C. Liu et al. (2006) nomment séparables des communautés dont les profils ne se croisent pas. Ils montrent que des communautés peuvent être séparables en selon un profil de diversité de \(^{q}\!D\) sans l’être forcément selon un profil de diversité de Hurlbert (section 3.4), et inversement. Ils montrent que les communautés séparables selon un troisième type de profil, celui de la queue de distribution (Patil et Taillie 1982), le sont dans tous les cas. Le profil de la queue de distribution est construit en classant les espèces de la plus fréquente à la plus rare et en traçant la probabilité qu’un individu appartienne à une espèce plus rare que l’espèce en abscisse (figure 4.6).

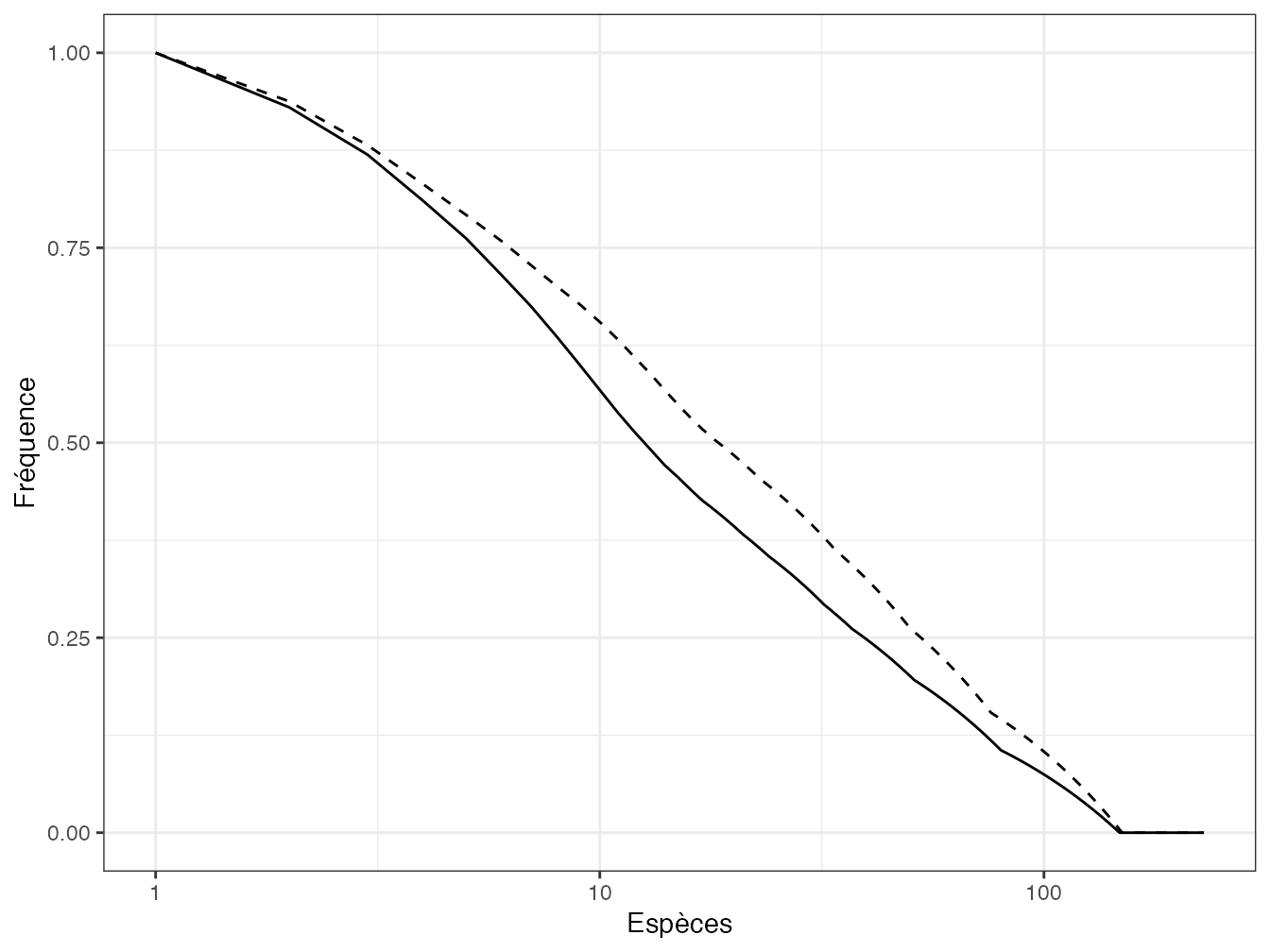
Figure 4.6: Profil de queue de distribution calculé pour les deux parcelles de Paracou (Parcelle 6 : trait plein et Parcelle 18 : trait pointillé). En abscisse : rang de l’espèce dans le classement de la plus fréquente à la plus rare ; en ordonnée : probabilité qu’un individu de la communauté appartienne à une espèce plus rare.

Code R :

# Elimination des espèces absentes des deux parcelles
Psi <- as.data.frame(Paracou618.MC$Psi[Paracou618.MC$Ps > 0,
    ])
Psi[, 1] %<>%
    sort %>%
    cumsum %>%
    rev
Psi[, 2] %<>%
    sort %>%
    cumsum %>%
    rev
Psi$x <- 1:nrow(Psi)
ggplot(Psi, aes(x)) + geom_path(aes(y = P006)) + geom_path(aes(y = P018),
    lty = 2) + labs(x = "Espèces", y = "Fréquence") + scale_x_log10()

Les coordonnées des points du profil sont définies par \[\begin{equation} \tag{4.21} y(x) = \sum_{s=x+1}^{S}{p_{[s]}},\ x\in \{0, 1, \dots, S\}. \end{equation}\]

\(p_{[s]}\) est la probabilité de l’espèce \(s\) ; les espèces sont classées par probabilité décroissante.

Ce profil est exhaustif (toutes les espèces sont représentées) alors que les autres profils de diversité ne sont représentés que pour un intervalle restreint du paramètre et qu’un croisement de courbes peut se produire au-delà. En revanche, il ne prend pas en compte les espèces non observées.

Fattorini et Marcheselli (1999) proposent un test pour comparer deux profils de queue de distribution à partir d’échantillonnages multiples (nécessaires pour évaluer la variance de chacune des probabilités) mais qui néglige les espèces non observées.

4.6 Estimation de l’entropie

4.6.1 Zhang et Grabchak

Z. Zhang et Grabchak (2016) montrent que toutes les mesures d’entropie usuelles sont des combinaisons linéaires de \({\zeta}_{u,v}\) (3.38). À partir des estimateurs de \({\zeta}_{u,v}\) (Z. Zhang et Zhou 2010), l’estimateur suivant est proposé pour \(h_q=\sum^S_{s=1}{p^q_s}\) :

\[\begin{equation} \tag{4.22} \tilde{h}_q = 1+\sum^{s^{n}_{\ne 0}}_{s=1}{\frac{n_s}{n}\sum^{n-n_s}_{v=1}{\left[\prod^v_{i=1}{\frac{i-q}{i}}\right]\left[\prod^v_{j=1}{\left(1-\frac{n_s-1}{n-j}\right)}\right]}}. \end{equation}\]

\(\tilde{h}_q\) peut ensuite être utilisé pour l’estimation de l’entropie HCDT : \[\begin{equation} \tag{4.23} ^q\!{\tilde{H}} = \frac{1-\tilde{h}_q}{q-1}. \end{equation}\]

L’estimateur est asymptotiquement normal et son biais décroit exponentiellement vite.

\(\tilde{h}_q\) n’est défini que pour \(q\ne 1\). L’estimateur corrigé de \(^{1}\!H\) est

\[\begin{equation} \tag{4.24} ^1\!{\tilde{H}} =\sum^{s^{n}_{\ne 0}}_{s=1}{\frac{n_s}{n}\sum^{n-n_s}_{v=1}{\frac{1}{v}\left[\prod^v_{j=1}{1-\frac{n_s-1}{n-j}}\right]}}. \end{equation}\]

Cet estimateur est différent de \(H_z\) (Z. Zhang 2012). Il a été également obtenu par d’autres auteurs (Mao 2007; Vinck et al. 2012; Chao, Wang, et Jost 2013, Annexe S1) avec d’autres approches.

Dans entropart, utiliser Tsallis et Diversity :

Tsallis(Paracou618.MC$Ns, q = 1, Correction = "ZhangGrabchak")

## ZhangGrabchak 
##      4.846407

Diversity(Paracou618.MC$Ns, q = 1, Correction = "ZhangGrabchak")

## ZhangGrabchak 
##      127.2823

4.6.2 Chao et Jost

Chao et Jost (2015) complètent cet estimateur par une estimation du biais résiduel, selon la même démarche que pour l’entropie de Shannon (Chao, Wang, et Jost 2013). \(h_q\) s’écrit sous la forme de la somme infinie des entropies de Simpson généralisées : \(h_q = \sum_{k=0}^{\infty}{\binom{q-1}{k}(-1)^k\zeta_{1,k}}\). Alors que l’estimateur de Zhang et Grabchak ne prend en compte que les \(n-1\) premiers termes de la somme pour un estimateur sans biais ; Chao et Jost (2015), eqn 5, le complètent par une estimation, forcément biaisée, des termes suivants pour obtenir :

\[\begin{align} \tag{4.25} ^q\!{\tilde{H}} = &\frac{1}{q-1} \\ &\left[ 1 -\tilde{h}_q -\frac{s_{1}}{n} {\left( 1-A \right)}^{1-n} \left( A^{q-1} -\sum^{n-1}_{r=0}{ \binom{q-1}{r} {\left(A-1\right)}^r} \right) \right]. \end{align}\]

La formule du nombre de combinaisons est généralisée aux valeurs de \(q-1\) non entières, et vaut par convention 1 pour \(r=0\). \(A\) vaut :

• \(2s_{2}/{\left[\left(n-1\right) s_{1} +2s_{2}\right]}\) en présence de singletons et doubletons ;
• \(2/{\left[\left(n-1\right)\left(s_{1} -1\right)+2\right]}\) en présence de singletons seulement ;
• \(1\) en absence de singletons et doubletons.

Cet estimateur est le plus performant. Quand \(q \to 1\), il tend vers l’estimateur de l’entropie de Shannon de Chao, Wang, et Jost (2013), équation (3.41). Quand \(q=0\), l’estimateur se réduit à Chao1. Pour toutes les valeurs entières de \(q\) supérieures ou égales à 2, il se réduit à l’estimateur (4.23), identique à l’estimateur de Lande pour \(q=2\), et est sans biais.

L’estimateur est obtenu à partir de celui du taux de couverture extrapolé (section 2.3) fourni par Chao et Jost (2012), annexe E, sans le détail de la démonstration présenté ici. L’espérance conditionnelle du taux de couverture dans un échantillon de taille \(n+m\) compte-tenu des effectifs observés, notés \(\{n_s\}\), est

\[\begin{equation} \tag{4.26} {\mathbb E}\left(C^{n+m} | \{n_s\} \right) = C^{n} + \sum_s{p_s [1-(1-p_s)^m] \mathbf{1}(n_s=0)}. \end{equation}\]

Le taux de couverture \(C^{n}\) est augmenté par l’échantillonnage de \(m\) individus supplémentaires si les espèces non échantillonnées (vérifiant \(\mathbf{1}(n_s=0)\)) sont découvertes (la probabilité de le faire est \(1-(1-p_s)^m\)).

\(\hat{C}^{n} + \sum_s{p_s \mathbf{1}(n_s=0)}\) vaut par définition 1.

Le deuxième terme de la somme est estimé en posant \(\hat{p}_s = \hat{\alpha}_0\) pour toutes les espèces non observées, ce qui constitue la même approximation que pour l’estimation de la relation de Good-Turing, équation (2.2). Alors, \((1-p_s)^m\) est estimé par \((1-\hat{\alpha}_0)^m\) et peut sortir de la somme qui ne contient plus que le terme \(\sum_s{p_s}\mathbf{1}(n_s=0)\), estimé par \(\hat{\alpha}_0 {s^{n}_{0}} = \frac{s^{n}_{1}}{n}(1 - \hat{\alpha}_1)\).

Les deux estimateurs \(\hat{\alpha}_1\) et \(\hat{\alpha}_0\) sont égaux à \(A\) si le nombre d’espèces non échantillonnées est estimé par l’estimateur Chao1. On obtient

\[\begin{align} \tag{4.27} {\mathbb E}\left(C^{n+m} \right) &= 1-\frac{s^{n}_{1}}{n} \left[ \frac{\left(n-1\right)s^{n}_{1}}{\left(n-1\right)s^{n}_{1}+2s^{n}_{2}} \right]^{n+m} \\ &= 1-\frac{s^{n}_{1}}{n} \left( 1-A \right)^{m+1}. \end{align}\]

L’espérance du taux de couverture est directement liée à l’indice de Simpson généralisé (Good 1953) : \({\mathbb E}(C^{n+m}) = 1 - \zeta_{1,n+m}\). L’estimateur de \(h_q\) est obtenu en remplaçant les termes \(\zeta_{1,k}\) de la somme infinie \(\sum_{k=n}^{\infty}{\binom{q-1}{k}(-1)^k \zeta_{1,k}}\) par la valeur de \(1 -{\mathbb E}(C^{n+m})\) calculée dans l’équation (4.27). La formule obtenue contient le développement en série entière de \([1 - (1-A)^{q-1}]\), ce qui permet d’éliminer la somme infinie et d’obtenir l’estimateur de l’équation (4.25) après simplifications (Chao et Jost 2015, Appendix S1, Theorem S1.2d).

4.6.3 Autres méthodes

Deux autres approches sont possibles (Marcon et al. 2014) :

• Celle de Chao et Shen (2003), étendue au-delà de l’entropie de Shannon qui prend en compte les espèces non observées ;
• Celle de Grassberger (1988) qui prend en compte la non-linéarité de l’estimateur.

Le domaine de validité des deux corrections est différent. Quand \(q\) est petit, les espèces rares non observées ont une grande importance alors que \(^{q}\!H\) est presque linéaire : la correction de Grassberger disparaît quand \(q=0\). Quand \(q\) est grand (au-delà de 2), l’influence des espèces rares est faible, la correction de Chao et Shen devient négligeable alors que la non-linéarité augmente. Un compromis raisonnable consiste à utiliser le plus grand des deux estimateurs.

L’estimateur de Chao et Shen est

\[\begin{equation} \tag{4.28} ^q\!{\tilde{H}} =-\sum^{s^{n}_{\ne 0}}_{s=1}{\frac{\hat{C}{\hat{p}}_s \ln_q\left(\hat{C}{\hat{p}}_s\right)}{1-{\left(1-\hat{C}{\hat{p}}_s\right)}^n}}. \end{equation}\]

Celui de Grassberger est

\[\begin{equation} \tag{4.29} ^q\!{\tilde{H}} = \frac{1-\sum^{s^{n}_{\ne 0}}_{s=1}{\widetilde{p^q_s}}}{q-1}, \end{equation}\]

où

\[\begin{equation} \tag{4.30} \widetilde{p^q_s} = {n_s}^{-q} \left( \frac{\mathrm{\Gamma}\left(n_s +1\right)}{\mathrm{\Gamma}\left(n_s -q+1\right)} + \frac{{\left(-1\right)}^n \mathrm{\Gamma}\left(1+q\right)\sin{\pi q}}{\pi\left(n+1\right)} \right). \end{equation}\]

\(\mathrm{\Gamma}\left(\cdot\right)\) est la fonction gamma. L’estimateur est linéaire par rapport à \(\widetilde{p^q_s}\) : le problème original est donc résolu par la construction de l’estimateur de \(p^q_s\), mais celui-ci est biaisé également.

L’estimateur de Chao et Shen peut être amélioré (Marcon 2015) en estimant mieux les probabilités. Chao, Hsieh, et al. (2015) ont développé un estimateur de la distribution des probabilités à partir de l’estimation du taux de couverture généralisé. \(\hat{C}{\hat{p}}_s\) peut être remplacé par cet estimateur pour réduire le biais de l’estimateur de Chao et Shen.

Enfin, la distribution des espèces non échantillonnées peut être ajoutée en estimant leur nombre et en choisissant une loi. Chao, Hsieh, et al. (2015) ont utilisé l’estimateur Chao1 et une distribution géométrique. L’estimateur jackknife (Burnham et Overton 1979) est plus versatile parce que son ordre peut être adapté aux données quand l’effort d’échantillonnage est trop faible pour que l’estimateur Chao1 soit performant (Brose, Martinez, et Williams 2003). Un simple estimateur plug-in, appelé “estimateur révélé”, peut ensuite être appliqué à cette distribution révélée (Marcon 2015).

L’estimateur du taux de couverture généralisé ne fait aucune hypothèse sur les espèces non observées, et n’utilise que le taux de couverture et la technique de Horvitz-Thompson pour estimer leur contribution. L’estimateur révélé ne tente aucune correction mais utilise l’estimation la meilleure possible pour la distribution des probabilités.

4.6.4 Biais des estimateurs

Étant donné la distribution des probabilités des espèces dans la communauté, l’échantillon inventorié peut être considéré comme un tirage dans une loi multinomiale, qui contient pas toutes les espèces. Par simulation à partir d’une distribution connue, il est possible de tirer un grand nombre d’échantillons et de répéter l’estimation de la diversité sur chacun d’eux. La distribution de la valeur de l’échantillon permet de juger ses performances : son biais moyen (mesuré par rapport à la valeur de référence calculée à partir des probabilités choisies), et sa variabilité (évaluée par sa variance empirique sur les simulations). Un estimateur performant doit être peu biaisé mais aussi peu variable. L’erreur quadratique moyenne, somme du carré du biais et de la variance, ou sa racine carrée dont la dimension est celle des données (root mean square error : RMSE), est un bon critère de test (voir par exemple Chao, Wang, et Jost 2013, fig. 1).

Haegeman et al. (2013) proposent deux estimateurs de la diversité \(^{q}\!D\) à partir des courbes de raréfaction et d’extrapolation du nombre d’espèces. Les deux estimateurs bornent la vraie valeur de \(^{q}\!D\) (leur variabilité n’est pas prise en compte, mais elle est négligeable dans le cadre utilisé). L’estimateur minimal est très proche de celui de Chao et Jost, à la différence que les termes estimant le biais résiduel sont évalués par une approximation numérique. L’estimateur maximal suppose que tous les individus non échantillonnés appartiennent à une espèce nouvelle, ce qui est effectivement le pire cas possible. Les deux estimateurs sont appliqués à la diversité de communautés microbiennes (jusqu’à un million d’espèces distribuées selon une loi géométrique) et très sous-échantillonnées (un individu sur \(10^{10}\) dans le pire des cas).

Les résultats présentent de très grands intervalles d’estimation (de plusieurs ordres de grandeur) entre la borne inférieure et la borne supérieure, ce qui montre que la méthode est inutilisable pour \(q<1\) approximativement. L’estimateur minimal, qui correspond à l’état de l’art, sous-estime sévèrement la diversité quand l’échantillonnage est faible. L’estimateur maximal est excessivement conservateur (il est conçu pour borner l’estimation dans la pire hypothèse).

Aux ordres de diversité supérieurs, les estimateurs convergent : même avec de petits échantillons, même en supposant que la richesse de la communauté est la plus grande possible, l’estimation de la diversité est précise dès \(q=1\).

Dans des conditions moins difficiles, correspondant à des communautés moins riches (typiquement des forêts tropicales), l’estimation est précise dès \(q=0,5\) (Marcon 2015). Ces résultats sont développés plus loin.

4.6.5 Intervalle de confiance des estimateurs

À partir de données d’inventaire, l’estimation du biais est impossible (sinon, le biais serait simplement ajouté à l’estimateur pour le rendre sans biais). La variabilité de l’estimateur peut être évaluée en générant des communautés par bootstrap et en estimant leur diversité comme dans la méthode précédente. Les communautés peuvent être simulées par tirage dans une loi multinomiale respectant les probabilités observées (Marcon et al. 2012, 2014). L’inconvénient est que les espèces dont les probabilités sont petites ne sont pas tirées, ce qui entraîne un nouveau biais d’estimation. L’estimateur le corrige en partie, le biais d’estimation dû au non échantillonnage des espèces rares de la communauté (corrigé par l’estimateur appliqué aux données réelles) n’est pas accessible. Il est donc nécessaire de recentrer les valeurs obtenues par simulation autour de la valeur obtenue sur les données.

Chao et Jost (2015) proposent une méthode plus élaborée qui consiste à reconstituer la distribution des probabilités de la communauté réelle le mieux possible avant d’en tirer les échantillons simulés. L’estimateur naïf de la probabilité d’une espèce observée \(s\) est \(\hat{p}_s = {n_s}/{n}\). \(\hat{p}_s\) est sans biais mais comme on ne dispose que d’une réalisation de la loi, il est préférable de chercher un estimateur sans biais conditionnellement aux espèces observées. Il est obtenu par Chao, Wang, et Jost (2013) à partir de l’espérance conditionnelle de \({N_s}/{n}\) :

\[\begin{equation} \tag{4.31} {\mathbb E} \left( \frac{N_s}{n} | n_s>0 \right) = \frac{p_s}{1-(1-p_s)^n}. \end{equation}\]

L’estimateur de \(p_s\) obtenu est

\[\begin{equation} \tag{4.32} \tilde{p}_s = \frac{n_s}{n} \left[ {1-\hat{\lambda}\left(1-\frac{n_s}{n}\right)^n} \right], \end{equation}\]

où

\[\begin{equation} \tag{4.33} \hat{\lambda} = \frac{1-\hat{C}}{\sum_{s=1}^{s^{n}_{\ne 0}} {\frac{n_s}{n} \left(1-\frac{n_s}{n}\right)^n}}. \end{equation}\]

\(\lambda\) est un paramètre d’un modèle permettant d’estimer les valeurs de \(p_i\) à partir de leur espérance conditionnelle et des données. Le modèle complet est présenté par Chao, Hsieh, et al. (2015).

Les probabilités des espèces non observées sont considérées comme égales par souci de simplification et parce qu’elles influencent peu la variance des estimateurs. Leur somme est égale au déficit de couverture, et leur nombre estimé par Chao1.

L’intervalle de confiance de l’estimateur obtenu par cette technique à partir des données permet de connaître sa variabilité, mais pas son biais. Il n’est absolument pas garanti (et peu probable si l’échantillonnage est faible et \(q\) petit) que la vraie valeur de la diversité se trouve dans l’intervalle de confiance.

4.6.6 Pratique de l’estimation

La conversion de l’estimateur de l’entropie en estimateur de la diversité pose un nouveau problème puisque \(^{q}\!D\) n’est pas une transformation linéaire de \(^{q}\!H\). Ce dernier biais peut être négligé (Grassberger 1988) parce que \(^{q}\!H\), l’entropie, est la valeur moyenne de l’information de nombreuses espèces indépendantes et fluctue donc peu à cause de l’échantillonnage, contrairement aux estimateurs des probabilités.

Des simulations menées sur des distributions log-normale ou géométrique de richesse diverses avec des efforts d’échantillonnage variés permettent de tester les estimateurs dans des cas théoriques réalistes (Marcon 2015). Un résultat représentatif est donné ici.

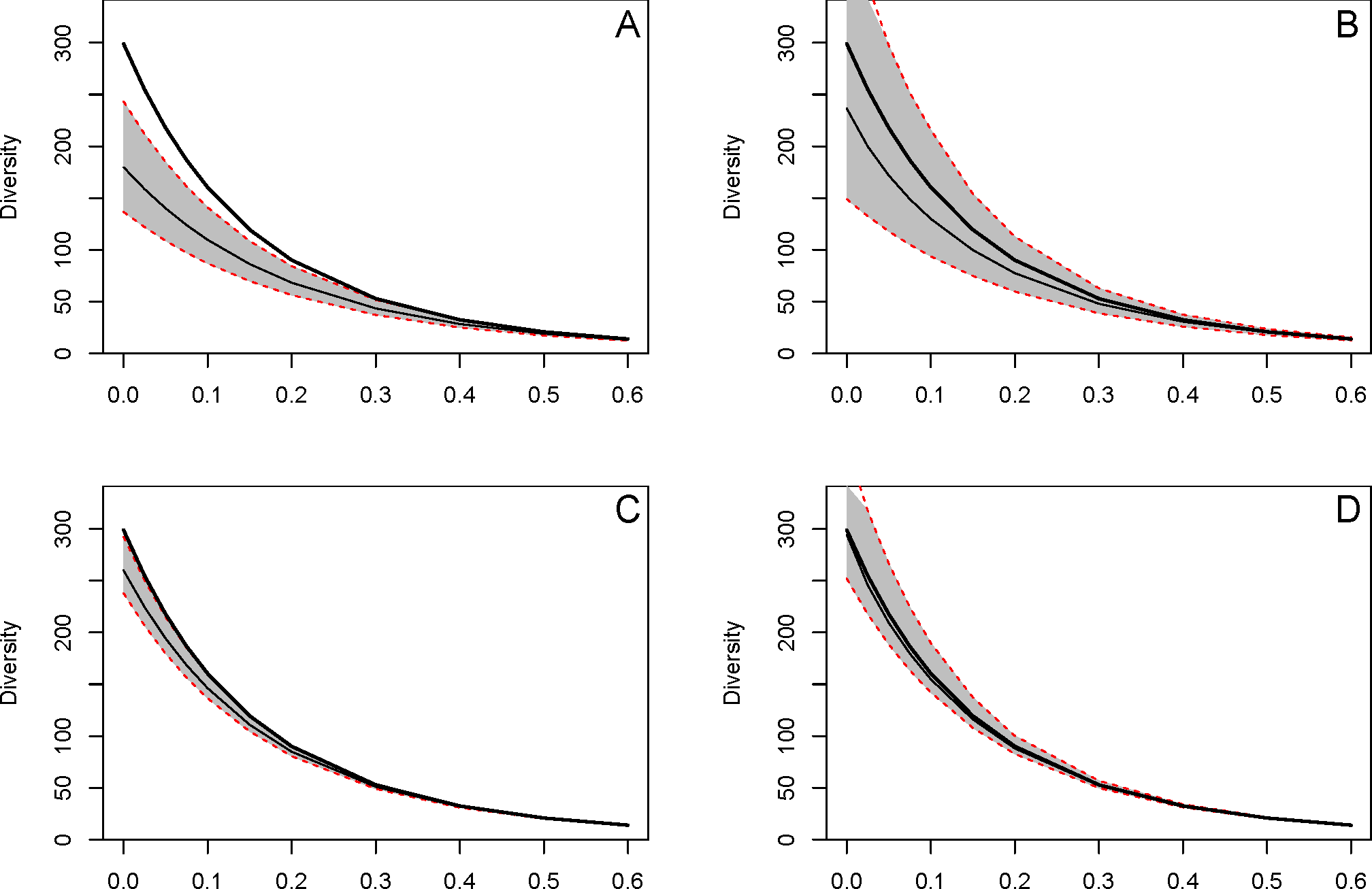
Figure 4.7: Estimation de la diversité d’une communauté log-normale de 300 espèces. Un inventaire de 500 (en bas) ou 5000 (en haut) individus est répété 1000 fois et la diversité estimée à chaque fois par l’estimateur de Chao-Wang-Jost (à gauche) ou l’estimateur révélé (à droite). La courbe noire en gras représente la vraie diversité de la communauté. La courbe maigre est la moyenne de l’estimation, l’enveloppe grise limitée par les pointillés rouges contient 95 % des valeurs simulées. A : 5000 individus, estimateur de Chao-Wang-Jost. B : 5000 individus, estimateur révélé. C : 500 individus, estimateur de Chao-Wang-Jost. D : 500 individus, estimateur révélé.

La figure 4.7 compare les résultats des deux meilleurs estimateurs à la vraie valeur de la diversité d’une communauté de 300 espèces, dont la distribution log-normale (avec un écart-type dont le logarithme vaut 2) mime une forêt tropicale similaire à Barro-Colorado. L’effort d’inventaire simulé est de 500 ou 5000 individus (de l’ordre d’un ou dix hectares pour les arbres de diamètre supérieur ou égal à 10 cm). L’estimation ne pose pas de problème avec 5000 individus, bien que Chao-Wang-Jost sous-estime un peu le nombre d’espèces. L’estimateur révélé est centré sur la vraie valeur, mais avec une plus grande variabilité.

En limitant l’échantillonnage à 500 individus, l’estimateur de Chao-Wang-Jost sous-estime le nombre d’espèces de moitié. L’estimateur révélé sous-estime beaucoup moins la diversité d’ordre faible, mais son intervalle de confiance est très large.

Dès \(q=0,5\), l’estimation est très précise dans tous les cas, même en réduisant l’échantillonnage à 200 individus ou pour des communautés dont la queue de distribution est beaucoup plus longue (résultats non présentés ici).

Les conclusions de ce travail d’évaluation tiennent en deux points. Dans des conditions réalistes d’inventaire d’arbres en forêt tropicale, les estimateurs de diversité les plus performants sont celui de Chao, Wang et Jost et l’estimateur révélé. Le premier a une variance plus faible pour les valeurs de \(q\) proches de 0 mais est limité par son estimation du nombre d’espèces par l’estimateur Chao1. Le second est préférable quand le nombre d’espèces estimé par l’estimateur jackknife d’ordre optimal est clairement supérieur (c’est-à-dire, en pratique, quand l’ordre du jackknife optimal est supérieur à 1). Son biais est alors bien inférieur, au prix d’une variance plus grande.

Dans tous les cas, l’estimation de la diversité aux ordres inférieurs à 0,5 est imprécise, sauf à disposer d’inventaires de taille considérable (de l’ordre de la dizaine d’hectares au moins).

Les fonctions Tsallis et Diversityde entropart acceptent comme argument un vecteur d’abondances (et non de probabilités) et proposent par défaut la correction de Chao et Jost :

Tsallis(colSums(BCI), q = 1)

##  UnveilJ 
## 4.276075

Diversity(colSums(BCI), q = 1)

##  UnveilJ 
## 71.95748

4.6.7 MSOM et MSAM

L’utilisation de modèles hiérarchiques bayesiens fondés sur des modèles d’occupation multispécifiques (MSOM) ou des modèles d’abondance multispécifiques (MSAM) progresse dans la littérature récente. Ils nécessitent de choisir une loi de probabilité d’observation des espèces compatible avec un échantillonnage non exhaustif, par exemple une loi ZIP (zero-inflated Poisson) (J. Zhang, Crist, et Hou 2014), dans laquelle l’espérance de la présence de chaque espèce peut être modélisée à son tour comme la conséquence de variables environnementales. Une approche alternative consiste à modéliser la probabilité d’observation comme la combinaison d’une probabilité de présence et d’une probabilité de détection (Broms, Hooten, et Fitzpatrick 2014). Ces méthodes ont l’avantage de fournir une distribution de probabilité des paramètres des modèles, et donc de la diversité qui est calculée comme une quantité dérivée. Leur faiblesse est qu’ils dépendent de la loi choisie. Une revue complète est fournie par Iknayan et al. (2014)

4.6.8 Raréfaction et extrapolation

Chao et al. (2014) étendent l’approche de Gotelli et Colwell (2001) aux nombres de Hill et fournissent les méthodes nécessaires au calcul de courbes de raréfaction et d’extrapolation de l’estimateur de \(^{q}\!D\) en fonction de la taille de l’échantillon ou du taux de couverture.

Les courbes de raréfaction sont obtenues à partir de l’échantillon disponible en simulant la diminution de sa taille. Les courbes d’extrapolation simulent l’augmentation de la taille de l’échantillon. Elles sont en réalité calculées par raréfaction d’un échantillon hypothétique de taille infinie : un estimateur de \(^{q}\!D\) corrigé du biais d’estimation est nécessaire. L’article se limite aux valeurs de \(q\) égales à 0, 1 ou 2 ou non entières mais supérieures à 2. Le package iNEXT (Hsieh, Ma, et Chao 2016) implémente ces calculs dans R comme le package entropart qui améliore l’estimation des ordres non entiers de diversité.

4.7 Autres approches

4.7.1 L’entropie de Rényi

L’entropie d’ordre \(q\) de Rényi (1961) est

\[\begin{equation} \tag{4.34} ^{q}\!R =\frac{1}{1-q\ln\sum^S_{q=1}{p^q_s}}. \end{equation}\]

C’est le logarithme naturel des nombres de Hill (1973) qui ont été définis à partir d’elle. L’entropie de Rényi a connu un succès important en tant que seule mesure d’entropie généralisée jusqu’à la diffusion de l’entropie HCDT. Son défaut est qu’elle n’est pas forcément concave (C. Beck 2009), ce qui empêche sa décomposition (voir chapitre 12).

4.7.2 L’entropie généralisée des mesures d’inégalité

L’entropie généralisée des économistes, d’ordre \(q\), est définie comme

\[\begin{equation} \tag{4.35} H_q = \frac{1}{q\left(q-1\right)} \left[\frac{1}{S}\sum^S_{s=1}{\left(\frac{n_s}{\bar{n_s}}\right)^{q}}-1\right]. \end{equation}\]

C’est en réalité une entropie relative, qui mesure l’écart entre la distribution observée \(\{n_s\}\) et sa valeur moyenne. Elle tend vers l’entropie de Theil quand \(q \to 1\) et la moyenne des \(\ln(\frac{n_s}{\bar{n_s}})\) quand \(q \to 0\). Elle a été conçue pour mesurer les inégalités (Cowell 2000), puis utilisée par exemple pour mesurer la concentration spatiale (Brülhart et Traeger 2005).

Maasoumi (1993) explicite cet usage et pour comparer la distribution de probabilité observée \(\{q_s\}\) à une distribution attendue \(\{p_s\}\), plutôt qu’à la distribution uniforme dont toutes les valeurs seraient \(\frac{1}{S}\). En posant \(r=q-1\), en transformant les abondances \(\{n_s\}\) en probabilités \(\{q_s\}\) et en choisissant \(\{p_s\}\) arbitrairement, on obtient

\[\begin{equation} \tag{4.36} H_r\left(\mathbf{q},\mathbf{p}\right) = \frac{1}{r\left(r+1\right)}\left[\sum^S_{s=1}{q_s{\left(\frac{q_s}{p_s}\right)}^{r}}-1\right]. \end{equation}\]

N. Cressie et Read (1984) ont défini une mesure généralisée de qualité d’ajustement (Goodness of Fit) de la distribution \(\{q_s\}\) à celle de \(\{p_s\}\). Elle est identique à l’entropie généralisée (à un coefficient 2 près) bien que développée indépendamment pour d’autres motivations. La statistique de Cressie et Read d’ordre 1 est la divergence de Kullback et Leibler (1951), celle d’ordre 2 le \(\chi^2\) de Pearson (1900).

Studeny et al. (2011) définissent une mesure d’équitabilité comme la divergence entre la distribution observée \(\{p_s\}\) et la distribution uniforme, ce qui les ramène à l’entropie de Cowell :

\[\begin{equation} \tag{4.37} I_r = \frac{1}{r\left(r+1\right)} \left[\sum^S_{s=1}{p_s \left(\frac{p_s}{1/S} \right)^{r}-1 } \right]. \end{equation}\]

Cette mesure inclut à la fois l’équitabilité et la richesse de la distribution. Il s’agit donc d’une mesure de diversité, qui est, à une normalisation près, l’écart entre la valeur de l’entropie HCDT d’ordre \(q=r+1\) et sa valeur maximale. Elle généralise donc l’indice de Theil (1967) :

\[\begin{equation} \tag{4.38} I_r = \frac{1}{q S^{1-q}}\left( \ln_q{S} - ^{q}\!H \right). \end{equation}\]

4.7.3 L’entropie de Simpson généralisée

L’entropie de Simpson généralisée a été introduite dans une classe d’indices plus générale (3.38) par Z. Zhang et Zhou (2010) et étudiée en détail par Z. Zhang et Grabchak (2016). L’entropie d’ordre \(r>0\) est \[\begin{equation} \tag{4.39} \zeta_r = \sum_{s=1}^S p_s (1-p_s)^r. \end{equation}\]

Elle se réduit à l’entropie de Simpson pour \(r=1\).

La fonction d’information de l’entropie de Simpson généralisée \(I(p)=(1-p)^r\) représente la probabilité de n’observer aucun individu de l’espèce de probabilité \(p\) dans un échantillon de taille \(r\) : c’est une mesure intuitive de la rareté. Chao, Wang, et Jost (2013) ont interprété \(\zeta_r\) comme la probabilité qu’un individu échantillonné au rang \(r+1\) appartienne à une espèce nouvelle dans une SAC. \((r+1)\zeta_r\) est aussi l’espérance du nombre de singletons dans un échantillon de taille \((r+1)\).

L’intérêt majeur de cette entropie est qu’elle dispose d’un estimateur non biaisé pour toutes les valeurs de \(r\) strictement inférieures à la taille de l’échantillon. C’est une mesure de diversité valide pour les ordres \(r\) strictement inférieurs au nombre d’espèces (Grabchak et al. 2017). Au-delà, elle ne respecte plus l’axiome d’équitabilité : sa valeur maximale n’est pas obtenue quand les espèces sont équiprobables.

Son nombre effectif d’espèces est \[\begin{equation} \tag{4.40} ^{r}\!D^{\zeta} = \frac{1}{1 - \zeta_r^{\frac{1}{r}}}. \end{equation}\]

L’existence d’un estimateur sans biais et d’un intervalle de confiance calculable analytiquement permet de comparer des profils de diversité de façon robuste quand l’échantillonnage est limité et la richesse élevée.

La figure 4.8a montre les profils de diversité (en nombre effectifs d’espèces) des deux parcelles 6 et 18 de Paracou : 1 ha inventorié, respectivement 681 et 483 arbres, pour une richesse estimée à 254 et 309 espèces par les estimateurs jackknife d’ordres 2 et 3 :

NsP6 <- as.AbdVector(Paracou618.MC$Nsi[, 1])
(S6 <- Richness(NsP6, Correction = "Jackknife"))

## Jackknife 2 
##         254

NsP18 <- as.AbdVector(Paracou618.MC$Nsi[, 2])
(S18 <- Richness(NsP18, Correction = "Jackknife"))

## Jackknife 3 
##         309

S <- min(S6, S18)

En comparaison, la figure 4.8b montre les profils de diversité HCDT des mêmes parcelles. Ils se chevauchent pour les petits ordres de diversité, ce qui ne permet pas de conclure.

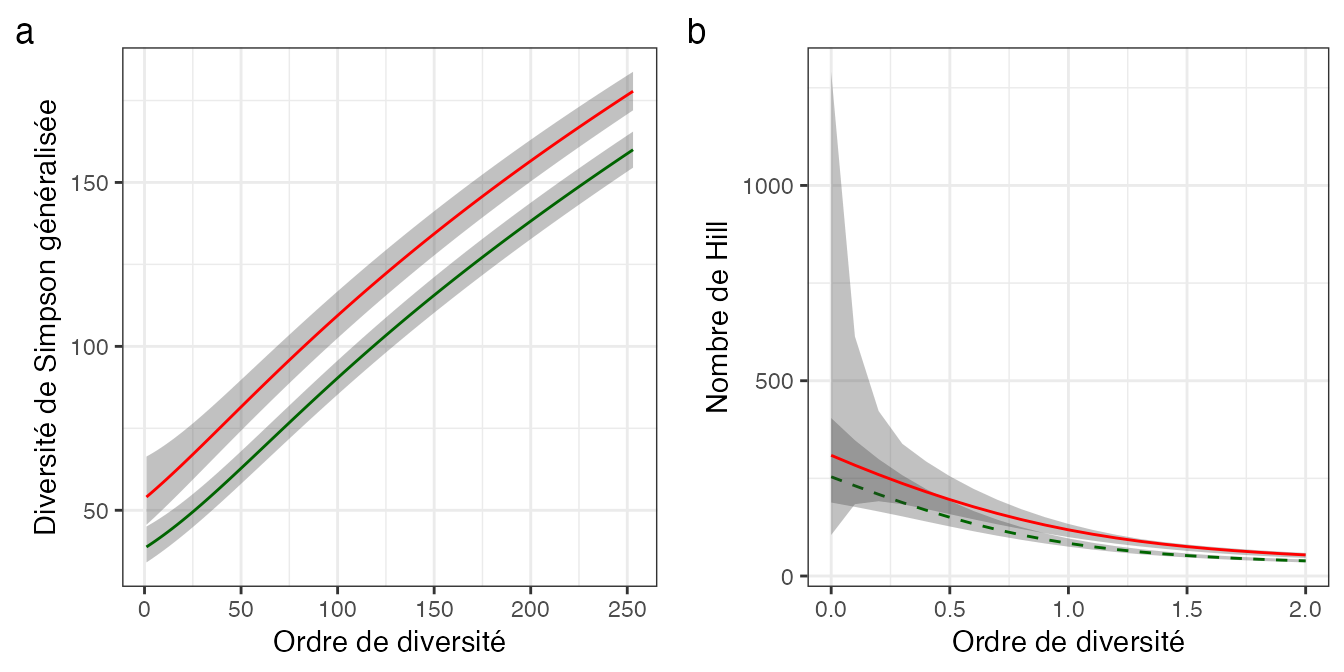
Figure 4.8: Comparaison des profils de diversité des parcelles 6 et 18 de Paracou avec leur intervalle de confiance à 95%. La parcelle 18 est tracée en rouge, lignes continues, et la 6 en vert, lignes pointillées. (a) Diversité généralisée de Simpson (nombres effectif d’espèces) : les profils sont distincts, ce qui permet de conclure que la parcelle 6 est plus diverse que la parcelle 18. (b) Diversité HCDT : les profils se chevauchent jusqu’à \(q \approx 0,7\).

La diversité est donc estimée jusqu’à l’ordre 253.

Code R pour réaliser la figure 4.8 :

# Profil P6
library("EntropyEstimation")
zeta6 <- CommunityProfile(GenSimpson, NsP6, 1:(S - 1))
sigma6 <- sapply(1:(S - 1), function(r) GenSimp.sd(NsP6, r))
ic6 <- qnorm(1 - 0.05/2) * sigma6/sqrt(sum(NsP6))
zeta6$low <- zeta6$y - ic6
zeta6$high <- zeta6$y + ic6
# Profil P18
zeta18 <- CommunityProfile(GenSimpson, NsP18, 1:(S - 1))
sigma18 <- sapply(1:(S - 1), function(r) GenSimp.sd(NsP18, r))
ic18 <- qnorm(1 - 0.05/2) * sigma18/sqrt(sum(NsP18))
zeta18$low <- zeta18$y - ic18
zeta18$high <- zeta18$y + ic18
# Transformation en diversité
zeta6D <- zeta6
zeta6D$y <- 1/(1 - (zeta6$y)^(1/zeta6$x))
zeta6D$low <- 1/(1 - (zeta6$low)^(1/zeta6$x))
zeta6D$high <- 1/(1 - (zeta6$high)^(1/zeta6$x))
zeta18D <- zeta18
zeta18D$y <- 1/(1 - (zeta18$y)^(1/zeta18$x))
zeta18D$low <- 1/(1 - (zeta18$low)^(1/zeta18$x))
zeta18D$high <- 1/(1 - (zeta18$high)^(1/zeta18$x))
# Figure
gga <- ggplot() + 
  geom_ribbon(aes(x, ymin = low, ymax = high), 
              as.data.frame.list(zeta18D), alpha = 0.3) +
  geom_line(aes(x, y), as.data.frame.list(zeta18D), col = "red") +
  geom_ribbon(aes(x, ymin = low, ymax = high), 
              as.data.frame.list(zeta6D), alpha = 0.3) +
  geom_line(aes(x, y), as.data.frame.list(zeta6D), col = "darkgreen") +
  labs(x = "Ordre de diversité", 
       y = "Diversité de Simpson généralisée") +
  labs(tag = "a")
# Calcul des profils HCDT
D6 <- CommunityProfile(Diversity, NsP6, NumberOfSimulations = 10,
q.seq=q.seq, Correction = "UnveilJ")
D18 <- CommunityProfile(Diversity, NsP18, NumberOfSimulations = 10,
q.seq=q.seq, Correction = "UnveilJ")
# Figure
ggb <- ggplot(data.frame(x = D6$x, D6$y, D18$y)) +
  geom_ribbon(aes(x, ymin = low, ymax = high), as.data.frame.list(D6), 
              alpha = 0.3) +
  geom_line(aes(x, D6.y), col = "darkgreen", lty = 2) + 
  geom_ribbon(aes(x, ymin = low, ymax = high), as.data.frame.list(D18), 
              alpha = 0.3) +
  geom_line(aes(x, D18.y), col = "red") + 
  labs(x = "Ordre de diversité", y = "Nombre de Hill") +
  labs(tag = "b")
grid.arrange(gga, ggb, ncol = 2)

La distribution statistique de la différence d’entropie est connue, et peut donc être tracée (figure 4.9). Son intervalle de confiance ne contient jamais la valeur 0, ce qui permet de conclure que la parcelle 18 est plus diverse.

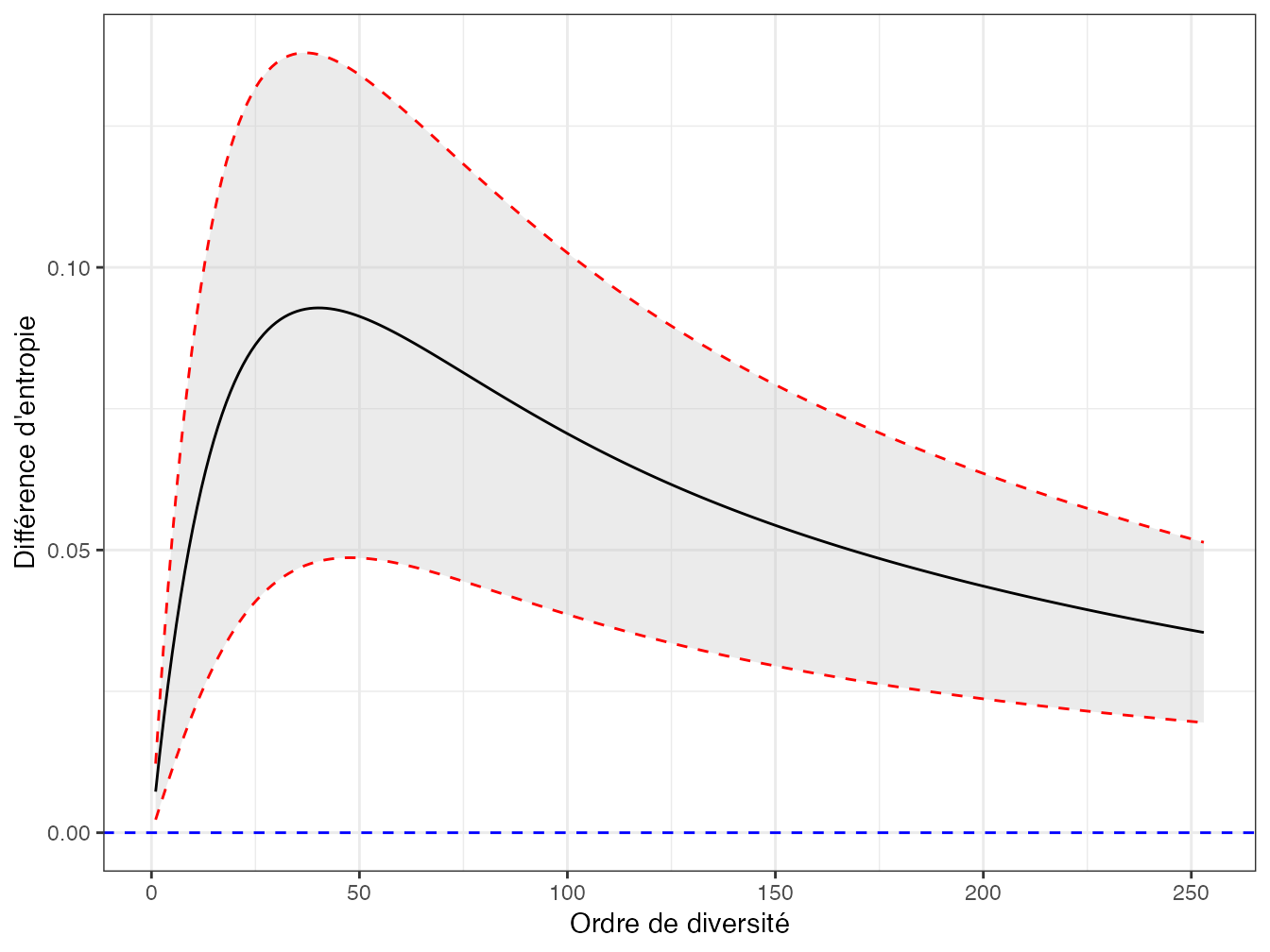
Figure 4.9: Différence entre les entropies de Simpson généralisées des parcelles 18 et 6 de Paracou avec son intervalle de confiance à 95%. La ligne horizontale représente l’hypothèse nulle d’égalité entre les entropies, qui peut être rejetée.

Code R pour réaliser la figure :

# Calcul de P18-P6 avec IC
  Difference <- list(x = zeta18$x, y = zeta18$y-zeta6$y)
  class(Difference) <- class(zeta18)
  icDifference <- qnorm(1-0.05/2)*sqrt(sigma6^2/sum(NsP6) 
                                       + sigma18^2/sum(NsP18))
  Difference$low <- Difference$y - icDifference
  Difference$high <- Difference$y + icDifference
  # Plot
  autoplot(Difference, xlab = "Ordre de diversité", 
           ylab = "Différence d'entropie") + 
    geom_hline(yintercept = 0, col = "blue", lty = 2)

La prise en compte des espèces rares est limitée par la valeur maximale de l’ordre \(r\) (limité à \(S-1\)). Les espèces plus rares ne peuvent pas être prises en compte : le profil de diversité s’arrête là. Le nombre effectif d’espèces maximum correspond au nombre de Hill d’ordre 0,5 environ. Les espèces plus rares sont prises en compte dans la partie du profil de diversité HCDT d’ordre inférieur à 0,5 mais son incertitude est grande et son biais très important quand l’échantillonnage est aussi réduit (Marcon 2015).

L’entropie de Simpson généralisée est donc l’outil le plus approprié pour comparer des profils de diversité de communautés riches et sous-échantillonnées.

4.7.4 L’entropie par cas

Rajaram et Castellani (2016) décomposent la diversité de Shannon en produit des contributions de chaque catégorie et proposent une mesure cumulative de la diversité d’une communauté prenant en compte une partie des espèces classées selon un critère pertinent, décrivant leur complexité : par exemple, la diversité des mammifères classés par taille croissante, ou la position dans l’évolution.

La fraction de la communauté dont le cumul des probabilités égale \(c\) est prise en compte. La diversité cumulée est : \[\begin{equation} \tag{4.41} \mathit{D_c} = \prod_c{p_s^{-p_s}}. \end{equation}\]

La mesure normalisée est appelée case-based entropy en anglais et vaut \[\begin{equation} \tag{4.42} \mathit{C_c} = \frac{100 D_c}{^{1}\!D}. \end{equation}\]

\(\mathit{D_c}={^{1}\!D}\) quand toute la communauté est prise en compte (\(c=1\)). Les auteurs s’intéressent principalement à la courbe de \(C_c\) en fonction de \(c\) pour montrer (Castellani et Rajaram 2016) que la contribution à la diversité totale des 40 % des composants les moints complexes de systèmes très divers (“des galaxies au gènes”) atteint toujours au moins 60%, ce résultat étant interprété comme une loi universelle de limitation de la complexité.

Cette mesure peut être étendue à l’entropie HCDT sans difficulté : \[\begin{equation} \tag{4.43} \mathit{^{q}\!C_{c}} = {\left(\sum_c{p^q_s}\right)}^{\frac{1}{1-q}}. \end{equation}\]

La méthode peut être appliquée pour évaluer la contribution de n’importe quel partie de la communauté à la diversité totale. Il ne s’agit pas d’une décomposition de la diversité au sens classique du terme, qui consiste à partitionner la diversité totale en diversité intra et inter-groupes, mais plutôt d’une façon de prendre en compte les caractéristiques des espèces dans une approche non-neutre.