7 Mesures particulières

De nombreuses mesures de diversité fonctionnelle ou phylogénétique ont été développées pour combiner le mieux possible la richesse et la régularité de la distribution des espèces dans l’espace des niches ou la phylogénie. Certaines (PD, FD, l’entropie quadratique de Rao, \(H_p\) et \(I_1\)) seront unifiées au chapitre suivant dans le cadre de l’entropie phylogénétique.

Un certain nombre de mesures de diversité phylogénétiques a émergé dans la littérature. Elles sont passées en revue ici, en commençant par la diversité fonctionnelle envisagée dans l’espace multidimensionnel des traits. Les sections suivantes envisagent les espèces dans un arbre phylogénétique.

7.1 Richesse, équitabilité et divergence fonctionnelle

Mason et al. (2005) postulent que la diversité fonctionnelle peut être abordée dans trois dimensions indépendantes (Jost (2010b) montrera que l’indépendance n’est pas assurée) :

• la richesse fonctionnelle, qui indique l’étendue de l’espace des niches fonctionnelles occupé par la communauté ;
• l’équitabilité de la distribution des espèces dans ces niches (appelée régularité par Pavoine et Bonsall (2011)) ;
• la divergence fonctionnelle, qui mesure comment la distribution des espèces dans l’espace des niches maximise la variabilité des caractéristiques fonctionnelles dans la communauté et combine richesse et équitabilité.

Schleuter et al. (2010) font une revue des mesures utilisées dans ce cadre. Les notations des indices utilisées ici sont les leurs.

Différents traits numériques sont connus pour toutes les espèces de la communauté. La matrice \(\mathbf{X}\) les contient : l’élément \(x_{t,s}\) est la valeur moyenne du trait \(t\) pour l’espèce \(s\). On note \(\mathbf{T}_s\) le vecteur des valeurs moyennes de chaque trait de l’espèce \(s\).

7.1.1 Richesse fonctionnelle

7.1.1.1 Étendue fonctionnelle

L’étendue fonctionnelle (Mason et al. 2005) mesure l’étendue des valeurs d’un trait occupée par une communauté, normalisée par l’étendue maximale possible : \[\begin{equation} \tag{7.1} \mathit{FR}_R = \dfrac{\max_s(x_{t,s}) - \min_s(x_{t,s})}{X_{t,max} - X_{t,min}}, \end{equation}\]

où \(\max_s(x_{t,s})\) est la valeur maximale pour toutes les espèces de la matrice de la valeur du trait \(t\), \(X_{t,max}\) est sa valeur maximale absolue (les notations sont identiques pour les minima). Les extrêmes absolus peuvent être ceux de l’ensemble des communautés comparées. Ils sont toujours sous-estimés : il est toujours possible théoriquement de trouver des valeurs plus extrêmes en augmentant l’effort d’échantillonnage. L’étendue fonctionnelle peut être moyennée sur plusieurs traits.

Schleuter et al. développent l’indice \(\mathit{FR}_{Is}\) pour prendre en compte la variabilité intraspécifique et les valeurs de traits non occupées par des espèces dans l’étendue fonctionnelle. Les valeurs de traits individuelles sont nécessaires : l’étendue des valeurs d’un trait est définie comme l’union des étendues des valeurs de chaque espèce.

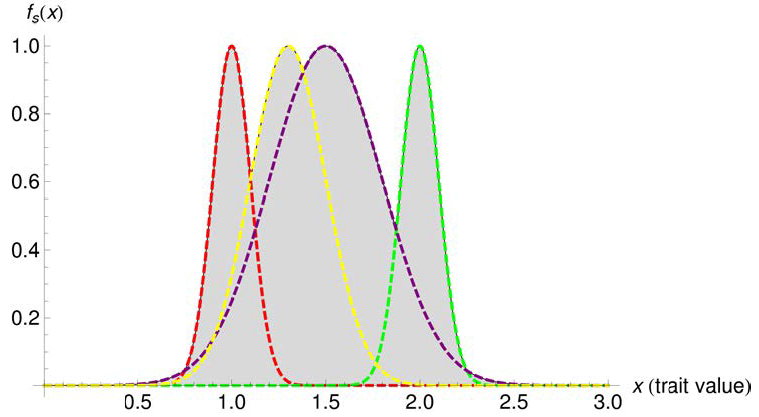
Figure 7.1: Fonction d’appartenance de l’espace des niches de Schleuter et al., en une dimension. \(x\), en ordonnée, est la valeur du trait considéré. Chaque espèce est considérée comme un ensemble flou dans l’espace des traits. Quatre espèces sont représentées, avec leur fonction d’appartenance \(f_s(x)\). Le volume de l’espace des traits occupé, \(\mathit{FR}_{Im}\), est obtenu en intégrant les fonctions d’appartenance : c’est la zone grisée de la figure.

7.1.1.2 Volume de niches

La définition de la niche écologique de Hutchinson (1957) est l’hypervolume, dans l’espace des ressources environnementales, qu’une espèce peut occuper. L’espace des traits fonctionnels peut être considéré comme une approximation de l’espace des ressources. Le volume de l’enveloppe convexe de l’espace des traits occupé par la communauté (convex hull volume) est donc une mesure de richesse fonctionnelle multidimensionnelle. La prise en compte des trous, c’est-à-dire la restriction du volume à l’espace réellement occupé à l’intérieur de cette enveloppe, est possible grâce à une méthode d’estimation d’hypervolume plus élaborée, implémentée dans le package hypervolume pour R (Blonder et al. 2014).

De même que pour l’étendue fonctionnelle, Schleuter et al. développent une mesure proche, \(\mathit{FR}_{Im}\), prenant en compte la variabilité intraspécifique et les espaces non occupés. Chaque espèce est supposée occuper un espace autour de sa position moyenne dans l’espace des traits, avec une fonction d’appartenance (Zadeh 1965) gaussienne multidimensionnelle (une représentation unidimensionnelle se trouve en figure 7.1, Schleuter et al. (2010)) : la fonction d’appartenance, issue de la logique floue, peut être vue comme une densité de probabilité non normalisée.

Les variances et covariances intraspécifiques des traits (rassemblés dans la matrice carrée \(\mathbf{\Sigma}_s\) de dimension \(t\) pour chaque espèce \(s\)) sont nécessaires. La fonction d’appartenance de l’espèce \(s\) dans l’espace des traits est, pour le vecteur \(\mathbf{T}\) de valeur de l’ensemble des traits : \[\begin{equation} f_s(\mathbf{T})= e^{-\frac{1}{2} \left(\mathbf{T}-\mathbf{T}_s \right)^\top \mathbf{\Sigma}_s^{-1} \left(\mathbf{T}-\mathbf{T}_s \right)}. \end{equation}\]

La richesse fonctionnelle est l’intégrale des valeurs maximales de \(f_s\) dans l’ensemble de l’espace des traits : \[\begin{equation} \tag{7.2} \mathit{FR}_{Im} = \int \max_s\left(f_s(\mathbf{T}) \right) \mathop{d\mathbf{T}}. \end{equation}\]

Après transformation de la matrice de distance en dendrogramme fonctionnel, éventuellement sous la forme d’un arbre-consensus (Mouchet et al. 2008), la longueur totale des branches, FD (Petchey et Gaston 2002), est une autre mesure de richesse multidimensionnelle.

7.1.2 Equitabilité fonctionnelle

L’équitabilité fonctionnelle, ou régularité (Pavoine et Bonsall 2011), rend compte de l’homogénéité de l’occupation des niches.

L’indice d’équitabilité de Mouillot, Mason, et al. (2005), que les auteurs nomment “indice de régularité fonctionnelle”, est inspiré de l’indice d’équitabilité de Bulla (5.1). C’est un indice unidimensionnel : un seul trait est pris en compte. Les espèces sont classées par valeur croissante du trait. L’équitabilité maximale est obtenue si l’écart entre deux valeurs de traits est proportionnel aux abondances cumulées des deux espèces. La statistique fondamentale est appelée équitabilité pondérée (weighted evenness). Pour l’intervalle entre l’espèce \(s\) et l’espèce \(s+1\) :

\[\begin{equation} \tag{7.3} \mathit{EW}_{s} = \frac{T_{s+1}-T_{s}}{N_{s+1}+N_{s}}. \end{equation}\]

Cette valeur est normalisée : \(\mathit{PEW}_{s}={\mathit{EW}_{s}}/{\sum_s{\mathit{EW}_{s}}}\). Sa valeur de \(\mathit{PEW}_{s}\) attendue pour le maximum d’équitabilité est \({1}/{(S-1)}\). L’indice est celui de Bulla, appliqué aux \(S-1\) intervalles entre espèces :

\[\begin{equation} \tag{7.4} \mathit{FE}_{s} = \sum_{s=1}^{S-1}{\min(\mathit{PEW}_{s},\frac{1}{S-1})}. \end{equation}\]

L’indice \(\mathit{FE}_{s}\) a été étendu pour être multidimensionnel par Villéger, Mason, et Mouillot (2008). L’arbre recouvrant de longueur minimum (minimum spanning tree) est d’abord calculé à partir des distances euclidiennes entre les espèces dans l’espace des traits : il s’agit de l’arbre de longueur totale minimale reliant tous les points. La longueur des branches est ensuite traitée de la même façon que \(\delta T_s\) précédemment.

Un autre indice, \({\Lambda}^+\) (Clarke et Warwick 2001), mesure la variance des distances entre paires d’espèces :

\[\begin{equation} \tag{7.5} {\Lambda}^+ =\frac{\sum_s{\sum_t{{\left(d_{s,t}-\hat{d}\right)}^2}}}{S\left(S-1\right)}. \end{equation}\]

Comme le montrent Mérigot et Gaertner (2011), les mesures de régularité n’ont absolument pas les mêmes propriétés que les mesures de diversité : elles peuvent par exemple augmenter quand on retire des espèces originales.

7.1.3 Divergence fonctionnelle

Les mesures de divergence fonctionnelle décrivent la variabilité de position des espèces dans l’espace des traits. Ce sont tout simplement des mesures de diversité au sens classique du terme.

Quand un seul trait est considéré, la mesure la plus simple est sa variance. Mason et al. (2003) effectuent une transformation logarithmique de la valeur du trait et pondèrent le calcul de la variance par les probabilités \(p_s\). Ils transforment finalement le résultat en son arc-tangente pour qu’il soit compris entre 0 et 1.

Schleuter et al. proposent d’utiliser la différence entre le troisième et le premier quartile de la valeur du trait, normalisée par son étendue maximale possible.

FAD a été proposé par B. Walker, Kinzig, et Langridge (1999), à partir d’une matrice de distances dans l’espace des traits. \(d_{s,t}\) est la distance entre deux espèces indicées par \(s\) et \(t\), alors :

\[\begin{equation} \tag{7.6} \mathit{FAD}=\sum_s{\sum_t{d_{s,t}}}. \end{equation}\]

FAD est très sensible au nombre d’espèces. Sa version normalisée, MFAD (Schmera, Erős, et Podani 2009) est

\[\begin{equation} \tag{7.7} \mathit{MFAD}=\frac{\sum_s{\sum_t{d_{s,t}}}}{S}. \end{equation}\]

Les deux indices violent l’axiome de jumelage. À un facteur de normalisation près, ce sont des cas particuliers de l’indice de Rao pour des effectifs égaux.

Le calcul sous R est immédiat avec un arbre au format phylog du package ade4. Un arbre au format phylo du package ape nécessite une conversion : la fonction Preprocess.Tree du package entropart la réalise.

phyTree <- Paracou618.Taxonomy
# La conversion as.hclust() double les distances. Il faut
# donc les diviser par deux.
phyTree$edge.length <- phyTree$edge.length/2
library("ape")

## 
## Attaching package: 'ape'

## The following objects are masked from 'package:spatstat.geom':
## 
##     edges, rotate

## The following object is masked from 'package:dplyr':
## 
##     where

# Conversion au format hclust
hTree <- as.hclust.phylo(phyTree)
# Conversion au format phylog
library("ade4")

## 
## Attaching package: 'ade4'

## The following object is masked from 'package:spatstat.geom':
## 
##     disc

Tree <- hclust2phylog(hTree)
# Tree$Wdist contient les valeurs de sqrt(2*distance)
(FAD <- sum(Tree$Wdist^2/2))

## [1] 264159

(MFAD <- FAD/length(Tree$leaves))

## [1] 621.5506

Kader et Perry (2007) regroupent les valeurs de trait par catégories et calculent l’entropie de Simpson des catégories.

Enfin, Villéger, Mason, et Mouillot (2008) utilisent la distance euclidienne moyenne des espèces au centre de gravité de la communauté plutôt que la variance. Précisément, le centre de gravité de la communauté (sans pondération par les fréquences) est calculé. La distance euclidienne de l’espèce \(s\) au centre de gravité est \(dG_s\) ; la moyenne pour toutes les espèces \(\bar{dG}\). L’écart moyen des individus de la communauté à la distance moyenne est \(\Delta d=\sum_s{p_s(dG_s - \bar{dG})}\). L’écart moyen absolu est \(\Delta |d|=\sum_s{p_s|dG_s - \bar{dG}|}\).

L’indice est \[\begin{equation} \tag{7.8} \mathit{FD}_{m} = \frac{\Delta d + \bar{dG}}{\Delta |d| +\bar{dG}}. \end{equation}\]

Sa forme lui permet d’être compris entre 0 et 1.

Laliberté et Legendre (2010) généralisent \(\mathit{FD}_{m}\) en proposant l’usage de n’importe quelle dissimilarité entre espèces, obtenue à partir de la méthode de Gower (vue en section 6.3), autorisant des variables qualitatives et des données manquantes, au-delà de la seule distance euclidienne entre traits quantitatifs. Ils fournissent le package FD pour calculer leur indice \(\mathit{FDis}\) et ceux de Villéger, Mason, et Mouillot (2008).

7.2 Originalité, richesse et équitabilité phylogénétique

La littérature de la diversité phylogénétique s’est intéressée tôt à l’originalité taxonomique des espèces parce que les questions traitées concernaient la conservation, concernée par la valeur de l’héritage évolutif (Faith 2008).

7.2.1 Mesures spécifiques d’originalité

Vane-Wright, Humphries, et Williams (1991) définissent la distinction taxonomique (taxonomic distinctness) \(\mathit{TD}_s\) de chaque espèce comme l’inverse du nombre de noeuds entre elle et la racine de l’arbre phylogénétique, normalisé pour que \(\sum_s{\mathit{TD}_s} = 1\). Dans l’arbre de la figure 7.2, les valeurs de TD non normalisées sont \({1}/{2}\) pour les deux premières espèces et \({1}/{3}\) pour les trois autres : la racine de l’arbre est comptabilisée dans le nombre de noeuds. Les valeurs de \(\mathit{TD}_s\) sont respectivement \({1}/{4}\) et \({1}/{6}\) après normalisation.

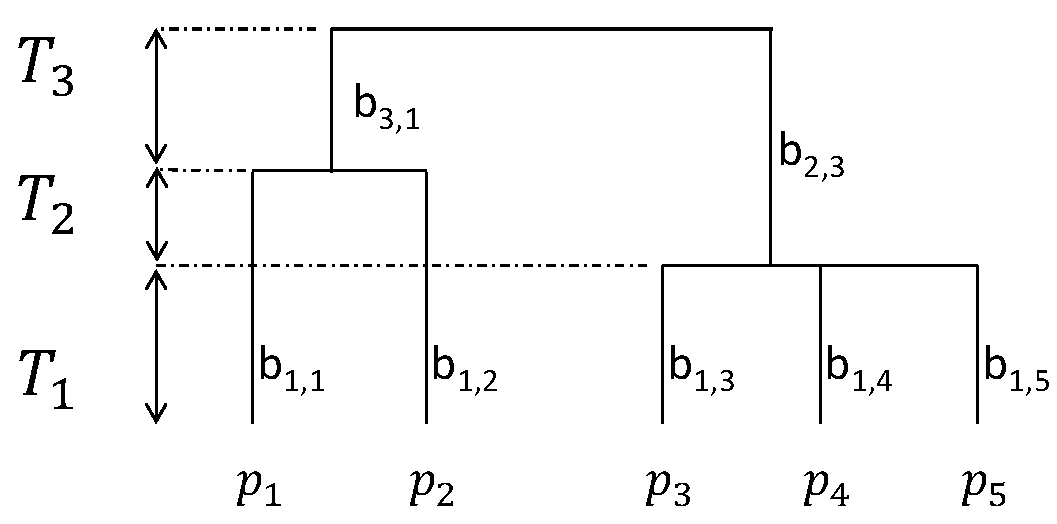
Figure 7.2: Arbre phylogénétique ou fonctionnel hypothétique. L’arbre comprend 5 espèces dont les probabilités sont notées \(p_s\), 3 périodes de durées \(T_k\) délimitées par les noeuds. Les branches sont notées \(b\) et indicées par la période à laquelle elles se terminent et un numéro d’ordre.

La particularité évolutive (Isaac et al. 2007) (evolutive distinctiveness, \(\mathit{ED}_s\)) de l’espèce \(s\) est la somme de la longueur des branches qui la relient à la racine de l’arbre, partagées entre tous les descendants de chaque branche. Pour l’espèce 3 de la figure 7.2, \(\mathit{ED}_3\) est égal à \(l(b_{1,3})\), la longueur de la branche terminale propre à l’espèce 3, plus un tiers de la longueur de la branche qui relie la racine de l’arbre à la polytomie dont l’espèce 3 est issue. Clairement, la diversité phylogénétique PD (section 7.5) est la somme des particularités évolutives de toutes les espèces de l’arbre.

7.2.2 Originalité taxonomique de Ricotta

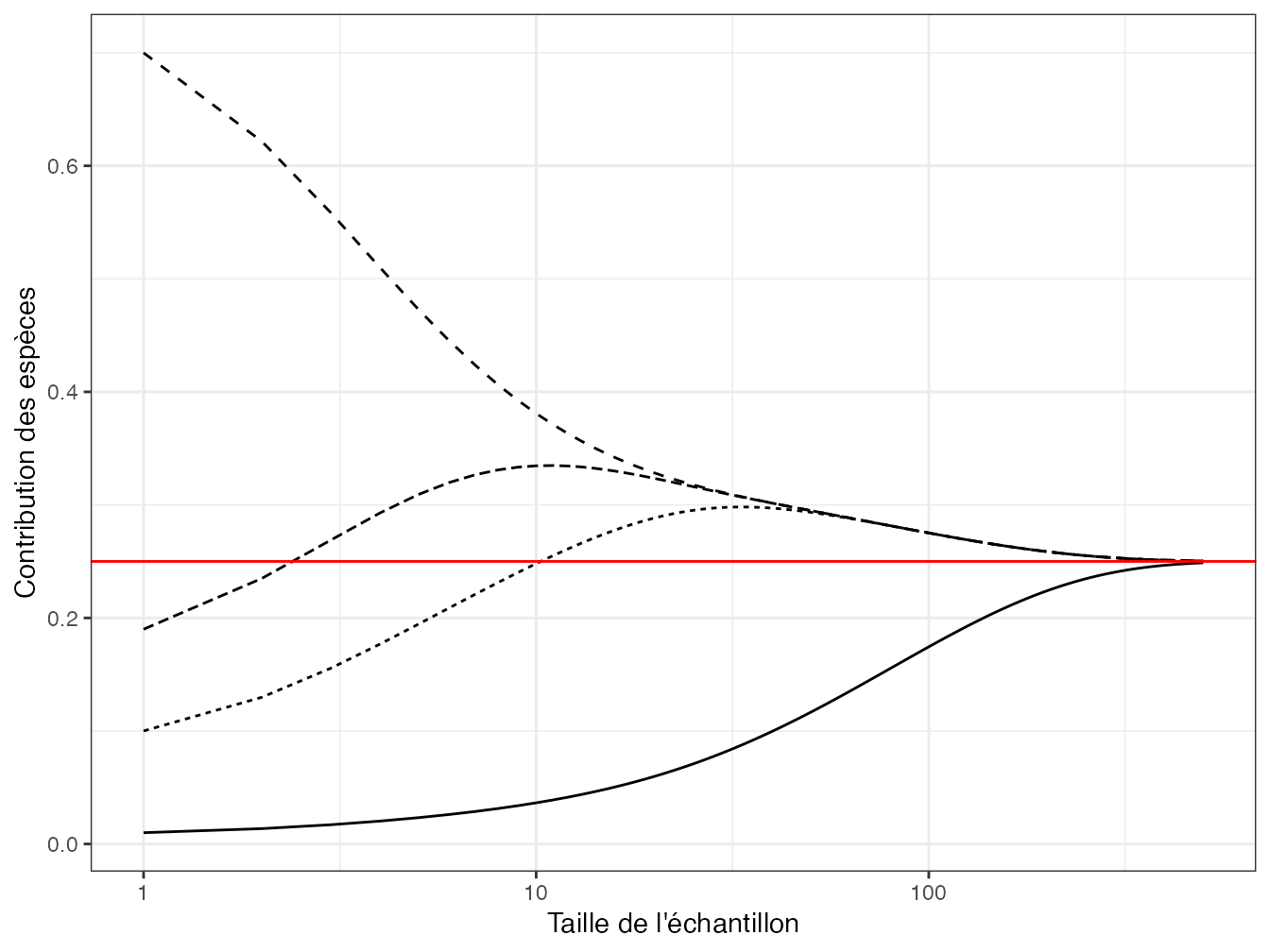
Figure 7.3: Contribution des espèces à l’indice de Hurlbert. Les contributions de 4 espèces d’une communauté à l’indice sont représentées en fonction de la taille de l’échantillon \(n\). Les fréquences des espèces sont lisibles pour \(n = 1\) : une espèce fréquente (probabilité égale à 0,7, supérieure à \(1/S\)), deux espèces peu fréquentes (0,19 et 0,1), et une espèce rare (0,01). Quand \(n\) est assez grand, toutes les contributions tendent vers \(1/S = 1/4\) (ligne horizontale).

Ricotta (2004a) construit un indice paramétrique (permettant de donner plus ou moins d’importance aux espèces rares) à partir de l’espérance du nombre d’espèces tirées dans un échantillon de taille \(n\) fixée (l’indice de Hurlbert (1971)) :

\[\begin{equation} \tag{7.9} {\mathbb E}\left( S^n \right) = \sum_s{\left[ 1-\left( 1-p_s \right)^n \right]}. \end{equation}\]

Ricotta pondère cette espérance par l’originalité taxonomique de chaque espèce, notée \(w_s\) et normalise la mesure : \[\begin{equation} \tag{7.10} ^n{T} = \frac{\sum_s{w_s \left[ 1-\left( 1-p_s \right)^n \right]}}{{\mathbb E}\left( S^n \right)}. \end{equation}\]

L’originalité taxonomique est définie comme la distance phylogénétique moyenne entre l’espèce \(s\) et les autres : \(w_s={\sum_s{d_{s,t}}}/{(S-1)}\).

Weikard, Punt, et Wesseler (2006) montrent que cette définition de \(w_s\) ne permet pas de satisfaire l’axiome de monotonicité d’ensemble. La définition correcte de \(w_s=\sum_s{d_{s,t}}\), validée par Ricotta (2006).

L’interprétation de \(^n{T}\) est plus intuitive en inversant la logique de sa construction.

\(w_s\) est l’originalité de l’espèce \(s\). \({[1-(1-p_s)^n]}/{{\mathbb E}(S^n)}\) est la contribution de l’espèce \(s\) à l’espérance du nombre d’espèces, comprise entre 0 et 1. \(^n{T}\) est donc l’originalité moyenne des espèces de la communauté, pondérée par la contribution de chaque espèce à l’espérance du nombre d’espèces observé, dans un échantillon de taille \(n\). Cette contribution est présentée en figure 7.3.

Quand \(n=1\), c’est simplement la fréquence des espèces. Quand \(n\) augmente, le poids des espèces fréquentes (dont la proabilité est supérieure à \(\frac{1}{S}\)) diminue alors que celui des espèces intermédiaires augmente. Ce dernier atteint \({1}/{{\mathbb E}(S^n)}\) (une espèce est échantillonnée à coup sûr dès que l’échantillon est assez grand) d’autant plus rapidement que \(p_s\) est grand. Il baisse ensuite alors que les espèces rares atteignent à leur tour progressivement leur poids maximal.

Quand \(n \to +\infty\), le numérateur tend vers FAD, et le dénominateur tend vers le nombre d’espèces : \(^n{T}\) tend vers MFAD.

Code R pour la figure 7.3 :

Ps <- c(0.7, 0.19, 0.1, 0.01)
S <- length(Ps)
nRange <- 1:500
# Indice de Hurlbert
ESn <- c(1, sapply(nRange[-1], function(n) Hurlbert(Ps, n)))
# Préparation du graphique
Xlab <- "Taille de l'échantillon"
Ylab <- "Contribution des espèces"
# Contribution de chaque espece à chaque valeur de n
Csn <- sapply(1:S, function(s) sapply(nRange, 
              function(n) (1-(1-Ps[s])^n))/ESn)
# Dataframe contenant les données
df <- as.data.frame(cbind(nRange, Csn))
colnames(df) <- c("n", "s07", "s019", "s01", "s001")
# Graphique
ESnplot <- ggplot(gather(df, Sp, Contribution, -n), aes(x=n)) +
  geom_line(aes(y = Contribution, lty=Sp)) +
  geom_hline(yintercept=1/4, col="red") +
  scale_x_log10() +
  labs(x = Xlab, y = Ylab) +
  theme(legend.position = "none")
ESnplot

7.2.3 Richesse phylogénétique

La particularité taxonomique moyenne (Warwick et Clarke 1995) (Average Taxonomic Distinctiveness, AvTD) est la distance moyenne dans l’arbre entre deux espèces choisies au hasard. C’est donc l’équivalent taxonomique de MFAD. La variabilité phylogénétique des espèces (Helmus et al. 2007) (Phylogenetic Species Variability, PSV) est la même mesure, obtenue à partir du modèle d’évolution suivant un mouvement brownien (Felsenstein 1985). La distance moyenne entre deux espèces est dans ce cadre proportionnelle à la covariance de leurs traits fonctionnels. La richesse phylogénétique des espèces, PSR, est PSV multipliée par le nombre d’espèces : c’est l’équivalent taxonomique de FAD.

La diversité FD de Faith (section 7.5), égale à la somme des longueurs des branches de l’arbre, semble avoir fait consensus, d’où un moindre développement des mesures de richesse que dans la littérature fonctionnelle.

7.2.4 Indices de Cadotte

Cadotte et al. (2010) proposent un ensemble de mesure phylogénétiques : équitabilité, déséquilibre d’abondance et diversité de la particularité evolutive.

7.2.4.1 Equitabilité phylogénétique

Les branches terminales de l’arbre phylogénétique sont ici à la base de la définition de l’équitabilité. figure 7.4, les branches \(b_{1,s}\) sont les segments terminés par une feuille (au bas de l’arbre), c’est-à-dire que leur longueur est la partie de l’arbre que les espèces ne partagent pas. La mesure d’équitabilité est \[\begin{equation} \mathit{PAE} = \frac{\mathit{PD} + \sum_s{l(b_{1,s})(n_s-1)}}{\mathit{PD} + (\frac{n}{S}-1)\sum_s{l(b_{1,s})} }. \end{equation}\]

Figure 7.4: Arbre phylogénétique ou fonctionnel hypothétique.

\(\mathit{PAE}\) vaut 1 quand les espèces sont sont distribuées équitablement pour la longueur des branches. Une valeur plus grande est obtenue quand les espèces sont concentrées au bout des longues branches, et inversement si \(0<\mathit{PAE}<1\).

7.2.4.2 Déséquilibre d’abondance

L’équilibre d’abondance est défini par une distribution aléatoire des espèces par division de l’effectif total à partir de la racine de l’arbre phylogénétique. En figure 7.4, en partant de la racine, la moitié des individus est supposée se répartir sur chaque branche. À la période 2, les effectifs de la branche de gauche se partagent en deux parties égales. À partir du nombre total d’individus de la communauté, \(n\), le nombre attendu d’individus \(n_s^0\) de l’espèce \(s\) est une fraction de \(n\) correspondant au nombre de noeuds et au nombre de branches partant de chaque noeud. On note \(y_{k,s}\) le nombre de branches partant du noeud ancestral de l’espèce \(s\) à la période \(k\), s’il existe, \(y_{k,s}=1\) sinon : \[\begin{equation} n_s^0 = \frac{n}{\prod_{k=2}^{K}{y_{k,s}}}. \end{equation}\]

En figure 7.4, pour l’espèce 3, \(y_{1,3}=3\) (l’espèce est issue d’une polytomie), \(y_{2,3}=1\) (absence de noeud) et \(y_{3,3}=2\) (la racine de l’arbre est dichotomique). On s’attend donc à ce que l’espèce 3 soit représentée par un sixième des individus.

L’indice de déséquilibre d’abondance mesure l’écart à cette distribution théorique : \[\begin{equation} \tag{7.11} \mathit{IAC} = \frac{\sum_s{|n_s - n_s^0|}}{\nu}. \end{equation}\]

\(\nu\) est le nombre de noeuds de l’arbre (3 dans l’exemple de la figure 7.4).

7.2.4.3 Diversité de la particularité évolutive

L’entropie de Shannon peut être appliquée pour mesurer la diversité des particularités évolutives : \[\begin{equation} \tag{7.12} H_{\mathit{ED}} = -\sum_s{\frac{\mathit{ED}_s}{\mathit{PD}} \ln\frac{\mathit{ED}_s}{\mathit{PD}}}. \end{equation}\]

L’équitabilité des particularités évolutives est celle de Pielou :

\[\begin{equation} \tag{7.13} E_{\mathit{ED}} = \frac{H_{\mathit{ED}}}{\ln{S}}. \end{equation}\]

Ces mesures ne prennent pas en compte les abondances des espèces. Pour y remédier, il suffit d’ajouter une période de durée nulle à chaque feuille de l’arbre, correspondant à une polytomie entre les \(n_s\) individus de chaque espèce. La particularité évolutive \(\mathit{AED}_s\) des individus de l’espèce \(s\), est calculée en partageant la longueur de chaque branche ancestrale entre le nombre d’individus qui en descendent (et non le nombre d’espèces). Alors \(\mathit{PD} = \sum_s{n_s \mathit{AED}_s}\). L’entropie devient \[\begin{equation} \tag{7.14} H_{\mathit{AED}} = -\sum_s{\frac{n_s \mathit{AED}_s}{\mathit{PD}} \ln\frac{n_s \mathit{AED}_s}{\mathit{PD}}} \end{equation}\] et l’équitabilité correspondante est \[\begin{equation} \tag{7.15} E_{\mathit{AED}} = \frac{H_{\mathit{AED}}}{\ln{N}}. \end{equation}\]

Ces indices ne mesurent pas la diversité phylogénétique au sens des autres mesures présentées dans ce chapitre. Ils mesurent la diversité de le particularité évolutive, autrement dit du temps d’évolution accumulé par chaque espèce ou chaque individu. Pour un nombre d’espèces fixé, \(E_{\mathit{ED}}\) atteint son maximum quand les valeurs de \(\mathit{ED}_s\) sont toutes identiques. Un arbre phylogénétique composé d’une seule branche depuis la racine terminé par une polytomie de longueur nulle portant toutes les espèces correspond à cette description. Dans cet exemple, les espèces ont une divergence évolutive nulle, mais \(E_{\mathit{ED}} = S\), son maximum possible.

7.3 Diversité de Scheiner

Scheiner (2012) développe un cadre unifié pour mesurer la diversité spécifique, phylogénétique ou fonctionnelle, séparément ou simultanément. L’idée générale est que toute quantité partagée par les espèces (le nombre d’individus, le temps d’évolution accumulé, la taille des niches écologique) peut être traduite en nombre de Hill.

La diversité spécifique est simplement \(^{q}\!D\). Scheiner la note \(^{q}\!D(A)\), pour diversité d’abondance.

La diversité phylogénétique \(^{q}\!D(P)\) ne prend pas en compte les abondances mais mesure la diversité de la divergence évolutive des espèces. La divergence totale dans un arbre phylogénétique (pas forcément ultramétrique) est la longueur totale des branches (c’est-à-dire FD). Elle est répartie entre toutes les espèces : la longueur de chaque branche (représentant une quantité d’évolution) est partagée à parts égales entre les espèces qui en descendent. La divergence de l’espèce 1 de la figure 7.7 est \(T1+T2\), la longueur de la branche terminale, plus \({T3}/{2}\), parce que la branche est partagée par les espèces 1 et 2. La divergence de l’espèce 1, est donc \(L_1 = T1+T2+{T3}/{2}\). La part de la divergence de l’espèce \(s\) est \(l_s = {L_s}/{FD}\). La diversité phylogénétique est le nombre de Hill des divergences :

\[\begin{equation} \tag{7.16} ^{q}\!D = {\left(\sum^S_{s=1}{l_s^q}\right)}^{\frac{1}{1-q}}. \end{equation}\]

La diversité fonctionnelle \(^{q}\!D(F)\) est la diversité des tailles des niches. La taille de la niche est définie par Scheiner comme le volume de l’hypersphère (dans l’espace des traits fonctionnels de dimension \(m\)) centrée sur chaque espèce dont le rayon est la moitié de la distance à l’espèce la plus proche pour que les sphères ne se superposent pas. Une meilleure définition (Presley, Scheiner, et Willig 2014) de la taille de la niche est la somme des distances aux autres espèces : \(t_s = \sum_t{d_{s,t}}\). La part de chaque espèce est \(f_s={t_s}/{\sum_t{t_t}}\) et la définition de la diversité fonctionnelle est

\[\begin{equation} \tag{7.17} ^{q}\!D(T) = {\left(\sum^S_{s=1}{f_s^q}\right)}^{\frac{1}{1-q}}. \end{equation}\]

La diversité peut prendre en compte plusieurs composantes, pas exemple l’abondance et la phylogénie pour définir

\[\begin{equation} \tag{7.18} ^{q}\!D(AP) = {\left(\sum^S_{s=1}{\left(\frac{n_s L_s}{\sum^S_{t=1}{n_t L_t}}\right)^q}\right)}^{\frac{1}{1-q}}. \end{equation}\]

La diversité d’abondance et phylogénétique est la diversité des divergences pondérées par les effectifs des espèces. La mesure de biodiversité de Scheiner, incluant les trois composantes, est

\[\begin{equation} \tag{7.19} ^{q}\!D(APF) = {\left(\sum^S_{s=1}{\left(\frac{n_s L_s t_s}{\sum^S_{t=1}{n_t L_t t_t}}\right)^q}\right)}^{\frac{1}{1-q}}. \end{equation}\]

Son interprétation est moins immédiate. Chaque espèce est associée à une fraction d’une des trois dimensions de la diversité (abondance, temps d’évolution cumulé, taille des niches). Elle occupe un parallélépipède de dimensions \((p_s, l_s, f_s)\) dans le cube de dimension 1 qui les contient toutes. Cette représentation ne donne pas d’importance particulière à l’abondance, et peut être appliquée à un nombre quelconque de dimensions. La mesure de biodiversité est la diversité des volumes occupés par les espèces, normalisés par leur somme (qui n’est pas égale à 1).

En se limitant à deux dimensions pour la lisibilité, la figure 7.5 présente les rectangles correspondant à la diversité d’abondance et fonctionnelle occupés par les espèces de la méta-communauté Paracou618, classées par fréquences décroissantes.

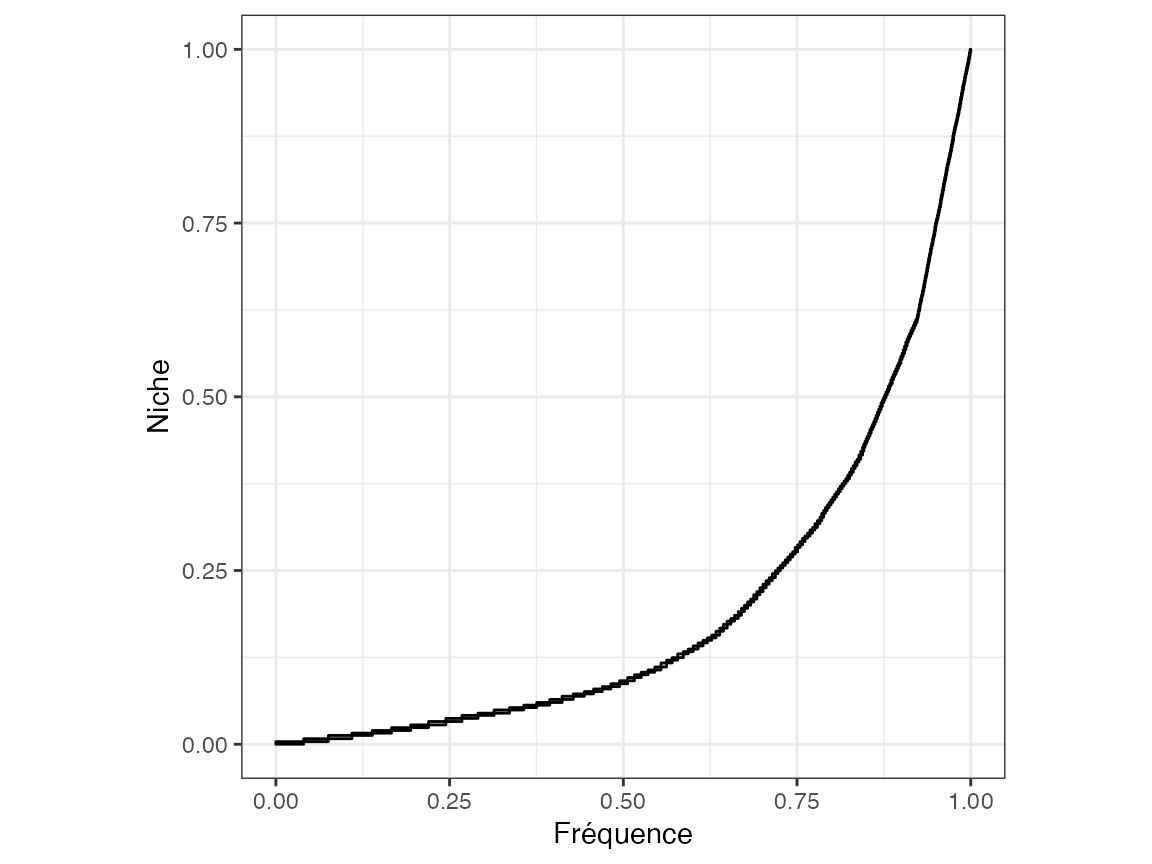
Figure 7.5: Rectangles de surface fréquence \(\times\) taille de niche des espèces de la méta-communauté Paracou618. La diversité de Scheiner \(^{q}\!D(AF)\) est la diversité de leur surface.

Code R :

# Probabilités
Ps <- Paracou618.MC$Ps[Paracou618.MC$Ps>0]
Ps <- sort(Ps, decreasing = TRUE)
# Fréquences cumulées
PsCum <- cumsum(Ps)
Xgauche <- c(0, PsCum)
Xdroite <- c(PsCum, 1)
# Matrice de distances fonctionnelles
DistanceMatrix <- as.matrix(Paracou618.dist)
# Mise en correspondance de la matrice et du vecteur de probabilités
DistanceMatrix <- DistanceMatrix[names(Ps), names(Ps)]
# Taille des niches
ts <- rowSums(DistanceMatrix)
fs <- ts/sum(ts)
# Fréquences cumulées
fsCum <- cumsum(fs)
Ybas <- c(0, fsCum)
Yhaut <- c(fsCum, 1)
# Rectangles occupés par chaque espèce
ggplot(data.frame(Xgauche, Ybas, Xdroite, Yhaut)) +
  geom_rect(aes(xmin= Xgauche, xmax= Xdroite, ymin= Ybas, ymax= Yhaut), 
             color = "black", fill = "white") +
  coord_fixed() +
  labs(x = "Fréquence", y="Niche")

La diversité d’abondance et fonctionnelle est la diversité de la surface des rectangles :

Surface <- Ps * fs
Rs <- Surface/sum(Surface)
Diversity(Rs, q = 2)

##     None 
## 71.72482

Le profil de diversité d’abondance et fonctionnelle est en figure 7.6.

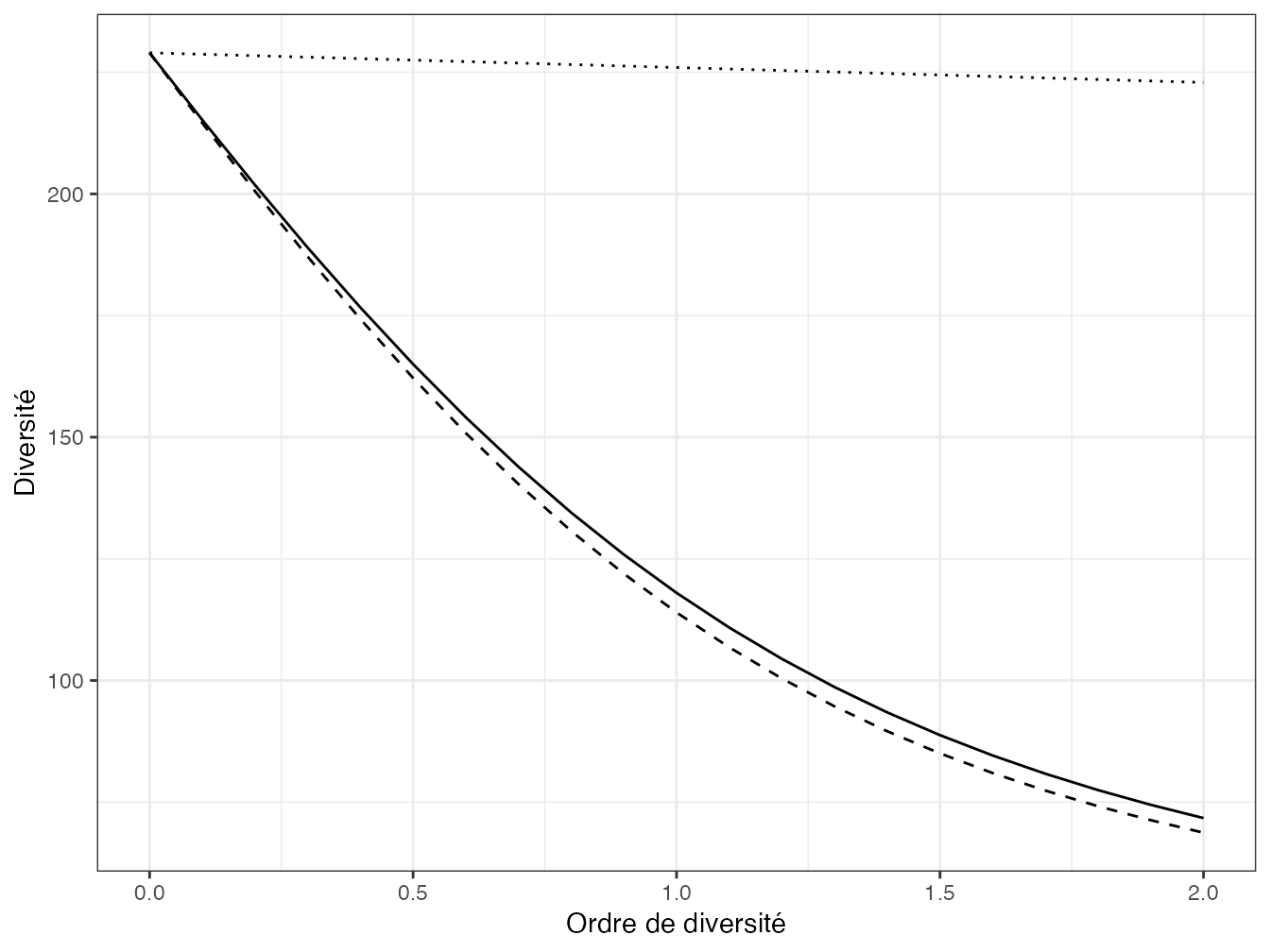
Figure 7.6: Profil de diversité d’abondance et fonctionnelle de Scheiner de la méta-communauté Paracou618. Pointillés longs : diversité d’abondance ; pointillés courts : diversité fonctionnelle ; trait plein : diversité d’abondance et fonctionnelle.

Code R :

autoplot(CommunityProfile(Diversity, Rs), 
         xlab="Ordre de diversité", ylab="Diversité") +
geom_line(data = as.data.frame.list(CommunityProfile(Diversity, Ps)), 
          mapping = aes(x, y), lty = 2) +
geom_line(data = as.data.frame.list(CommunityProfile(Diversity, fs)),
          mapping = aes(x, y), lty=3)

La notion de diversité phylogénétique ou fonctionnelle traitée par Scheiner est assez différente de celles vues précédemment parce qu’elle considère toutes les dimensions de façon symétrique : l’ordre de diversité, \(q\), s’applique à toutes les dimensions. Si \(q\) est grand, les espèces dont le produit des dimensions de la diversité est petit (que l’espèce soit rare, ait une divergence phylogénétique faible ou une niche étroite) sont négligées, alors que \(q\) n’affecte que la fréquence dans le cadre de la phylodiversité \(^{q}\!\bar{D}\) ou la banalité pour \(^q\!D^{\mathbf{Z}}\).

7.4 Diversité de Solow et Polasky

Solow et Polasky (1994) relient la richesse fonctionnelle ou phylogénétique à la probabilité de trouver au moins une espèce intéressante (par exemple, capable de fournir une molécule utile) dans une communauté.

Les distances entre espèces sont supposées connues, qu’elles soient fonctionnelle, phylogénétique ou autre. La probabilité qu’une espèce quelconque soit intéressante est fixée à \(p\), par exemple à partir de l’expérience passée (si une espèce criblée sur 100 fournit une molécule utile, \(p=1\%\)). En absence d’information sur les espèces, \(p\) est a priori identique pour toutes mais on suppose une corrélation entre les probabilités dépendant de la distance entre les espèces. Formellement, une fonction de similarité entre les espèces \(s\) et \(t\) est définie : \(z_{s,t}=f(d_{s,t})\). Cette fonction est décroissante entre 1 (quand la distance est nulle) et 0 (à distance infinie) ; par exemple \(f(d_{s,t}) = e^{-u d_{s,t}}\) où \(u\) est une constante strictement positive. La matrice \(\mathbf{Z}\) réunit les éléments \(z_{s,t}\).

On définit ensuite la variable de Bernoulli \(B_s\) (d’espérance \(p_s\)) qui vaut 1 si l’espèce \(s\) est intéressante. \(z_{s,t}\) est, par construction du modèle, la corrélation entre \(B_s\) et \(B_t\) : deux espèces très proches ont la même probabilité d’être intéressante, deux espèces très éloignées ont des probabilités indépendantes. La probabilité qu’au moins une espèce soit intéressante est minorée par \(p^2 \mathbf{1}_S' \mathbf{Z}^{-1} \mathbf{1}_S\), où \(\mathbf{1}_S\) est le vecteur de longueur \(S\) ne contenant que des 1, \('\) indique la transposée et \(\mathbf{Z}^{-1}\) est la matrice inverse de \(\mathbf{Z}\) (son existence est garantie puisque \(\mathbf{Z}\) est une matrice de variance-covariance). La valeur de \(p\) est incertaine et sans grand intérêt.

\(V = \mathbf{1}_S' \mathbf{Z}^{-1} \mathbf{1}_S\) est la mesure de diversité de Solow et Polasky. Elle rend compte de la dispersion des espèces : moins les espèces sont similaires, plus la probabilité que l’une d’elle au moins soit intéressante est élevée, conditionnellement au nombre d’espèces et à \(p\). Si les espèces sont infiniment éloignées les unes des autres, \(\mathbf{Z}\) est la matrice identité et la diversité est égale à la richesse : \(V\) est donc un nombre effectif d’espèces, c’est-à-dire le nombre d’espèces totalement dissimilaires nécessaires pour obtenir la diversité observée. À l’opposé, si toutes les espèces sont identiques, \(\mathbf{Z}\) ne contient que des 1 et la diversité vaut 1.

7.5 FD et PD

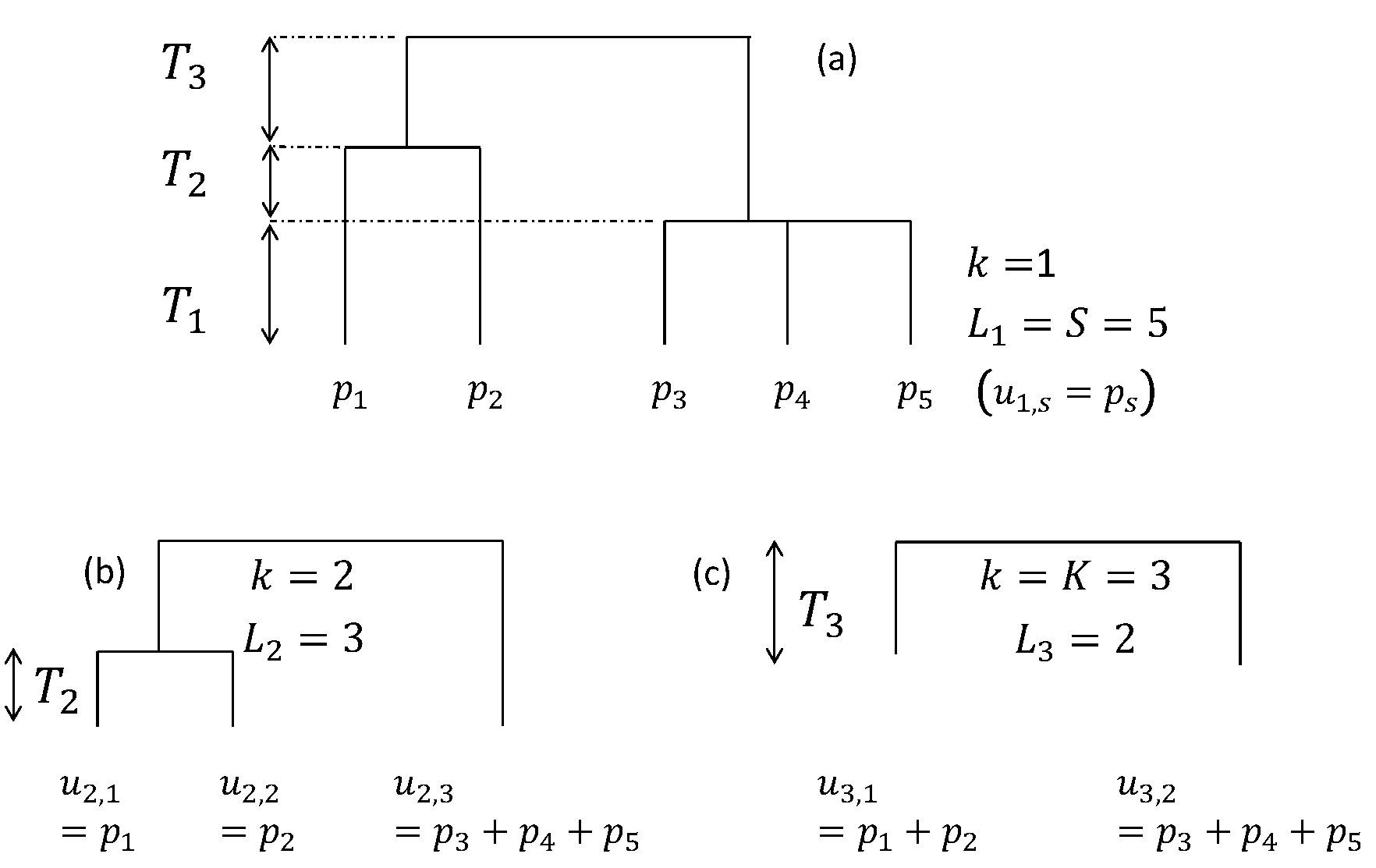
Figure 7.7: Arbre phylogénétique ou fonctionnel hypothétique. (a) Arbre complet. 5 espèces sont présentes (\(S = 5\)). Une période de l’arbre est définie entre deux noeuds successifs : l’arbre contient \(K = 3\) périodes. Les hauteurs des périodes sont notées \(T_k\). À chaque période correspond un arbre plus simple : (b) pour la période 2, (c) pour la période 3 dans lequel les espèces originales sont regroupées. Le nombre de feuilles de ces arbres est noté \(L_k\). Les probabilités pour un individu d’appartenir à une feuille sont notées \(u_{k,l}\).

Si la dissimilarité entre les espèces est représentée par un dendrogramme, les indices de diversité les plus simples sont la diversité phylogénétique (Faith 1992) et sa transposition, la diversité fonctionnelle (Petchey et Gaston 2002).

Étant donné un arbre contenant toutes les espèces ou tous les individus étudiés, PD ou FD sont égaux à la somme de la longueur des branches (figure 7.7 : \(\mathit{PD}=5\times T_1 + 3\times T_2 + 2\times T_3)\). Si les noeuds de l’arbre phylogénétique sont datés, PD peut être considéré comme une accumulation de temps d’évolution par la communauté étudiée : Sol et al. (2017) montrent par exemple que les milieux urbanisés ont un déficit de 450 millions d’années d’évolution dans les communautés d’oiseaux relativement aux environnements naturels voisins.

Dans le cas particulier ou toutes les branches sont de longueur 1, c’est-à-dire que toutes les espèces sont liées à la même racine (on dira que l’arbre est parfaitement régulier), PD et FD sont égales à la richesse spécifique.

Le package entropart fournit la fonction PDFD :

# Vecteur des probabilités
Ps <- Paracou618.MC$Ps
PDFD(Ps, Paracou618.Taxonomy)

## None 
##  395

Chao, Chiu, et al. (2015) fournissent un estimateur de PD (ou FD) permettant de l’estimer sans biais pour un échantillon plus petit que celui observé et de façon fiable pour un échantillon de taille double au maximum. Ces estimateurs permettent de tracer des courbes de raréfaction et d’extrapolation.

En même temps que Faith, Weitzman (1992) a établi une fonction de diversité identique à PD. À partir d’une matrice de dissimilarités entre espèces, un arbre est construit par la méthode suivante. Les deux espèces les plus proches sont rassemblées. L’une d’elles, celle qui diminue le moins la longueur totale des branches de l’arbre final en la retirant, est l’espèce de lien, l’autre est l’espèce représentative du clade. L’espèce de lien est retirée et le regroupement poursuivi entre les deux nouvelles espèces les plus proches. À chaque étape, l’espèce de lien est retirée jusqu’au regroupement final entre les deux dernières espèces. La difficulté est que l’arbre final n’est pas connu aux premiers stades de regroupement donc tous les arbres doivent être testés pour trouver la solution unique. La diversité est la somme des distances entre les espèces de lien et leur espèce représentative, c’est-à-dire la longueur totale des branches de l’arbre obtenu. L’application à la conservation est que les espèces représentatives doivent être favorisées par rapport aux espèces de lien ; en d’autres termes, les espèces dont les branches sont les plus courtes dans l’arbre sont celles qui apportent le moins de diversité. Ce résultat est assez évident quand on dispose d’un arbre phylogénétique. L’originalité de la méthode de Weitzman est de fournir un algorithme pour créer l’arbre à partir d’une matrice de distances qui est cohérent avec la mesure de diversité appliquée.

La mesure de diversité peut être combinée avec une probabilité d’extinction de chaque espèce (à dire d’expert) pour calculer l’espérance de la diversité à une échéance donnée (Weitzman 1993) : \(2^S\) arbres peuvent être construit en faisant disparaître certaines des \(S\) espèces de la communauté, la probabilité de chaque arbre est calculable à partir des probabilités d’extinction de chaque espèce (supposées indépendantes) et l’espérance de diversité est simplement la moyenne des diversités de chaque arbre pondérée par sa probabilité. L’espérance de la perte de diversité peut être calculée de façon plus simple (Witting et Loeschcke 1995), comme la moyenne de la longueur des branches pondérée par la probabilité de leur disparition, qui est le produit de la probabilité de disparition de toutes les espèces descendant de la branche.

Diverses optimisations économiques sont possibles, dont le choix des espèces à protéger à partir de l’élasticité de la diversité, c’est-à-dire le gain de diversité entraîné par la diminution de la probabilité de disparition de chaque espèce : les espèces ayant la plus grande élasticité sont celles sur lesquelles les efforts auront les plus grands résultats.

7.6 Indice de Rao

L’indice de Rao est une mesure de divergence pondérée. Son utilisation s’est largement développée depuis le début des années 2000 (Izsák et Papp 2000; Shimatani 2001b; Botta-Dukát 2005; Escalas et al. 2013) en raison de ses propriétés particulièrement intéressantes.

7.6.1 Principe

À partir de relevés fournissant la fréquence de chaque espèce par communauté et d’une matrice de dissimilarité entre paires d’espèces, l’indice de Rao (1982) donne la dissimilarité moyenne entre deux individus choisis au hasard.

L’indice de Rao est souvent appelé “entropie quadratique” en raison de sa forme mathématique.

7.6.2 Formalisation

Les espèces sont prises deux à deux et sont donc notées ici \(s'\) et \(s''\).

On note \(\mathbf{\Delta}\) la matrice de dissimilarité dont les éléments sont \(\delta_{s's''}\), la dissimilarité entre l’espèce \(s'\) et l’espèce \(s''\). Il n’est pas nécessaire à ce stade que \(\mathbf{\Delta}\) soit une distance. \(\mathbf{p}\) est le vecteur des probabilités dont \(p_{s'}\) et \(p_{s''}\) sont des éléments :

L’indice de Rao est

\[\begin{equation} \tag{7.20} H_{\mathbf{\Delta}}\left(\mathbf{p}\right)=\sum_{s'}{\sum_{s''}{p_{s'}}}p_{s''}\delta_{s's''}. \end{equation}\]

7.6.3 Propriétés

La définition de la distance est essentielle :

• en fixant \(\delta_{s's''}=1\) si deux espèces sont différentes, on obtient l’indice de Simpson. Sa valeur peut être interprétée comme la probabilité qu’une paire d’individus choisie au hasard soit de deux espèces différentes ;
• Dans un espace unidimensionnel où la valeur \(y_s\) associée à l’espèce \(s\) est une variable quantitative \(Y\), choisir \(\delta_{s's''}={{\left(y_k-y_l\right)}^2}/{2}\) rend l’indice de Rao égal à la variance de \(Y\).

Pavoine, Ollier, et Pontier (2005) ont montré que l’utilisation de distances ordinaires fait que la valeur maximale de l’entropie quadratique pour un effectif donné est obtenue en éliminant les espèces intermédiaires en ne retenant que les espèces extrêmes (le résultat est évident en une dimension : la variance est maximale en ne retenant que les valeurs extrêmes d’un échantillon). Ce résultat est contraire aux propriétés attendues d’un indice de diversité. Les auteurs ont établi que l’utilisation de distances ultramétriques corrige ce défaut. L’indice atteint alors son maximum pour des fréquences d’autant plus grandes que l’espèce est originale (Pavoine, Ollier, et Dufour 2005).

L’estimation empirique de l’indice se fait simplement en estimant les probabilités par les fréquences. Le biais d’estimation est très faible (Marcon et al. 2014) : par analogie avec l’estimateur de l’indice de Simpson, les espèces rares interviennent peu.

7.6.4 Calcul sous R

Le package entropart fournit la fonction Rao :

# Vecteur des probabilités
Ps <- Paracou618.MC$Ps
Rao(Ps, Paracou618.Taxonomy)

##     None 
## 2.878133

Le package ADE4 permet le calcul avec la fonction divc qui utilise un format différent pour les probabilités et surtout la matrice des racines carrées du double des distances de l’objet phylog (chaque élément de \$Wdist vaut \(\sqrt{2\delta_{s's''}}\). Cette particularité d’ADE4 vient de l’analyse multivariée (Champely et Chessel 2002) : l’entropie quadratique de Rao peut être représentée dans l’espace euclidien engendré par une matrice de distances \(\mathbf{D}\) entre espèces (par une Analyse en Coordonnées Principales, PCoA). L’inertie des points représentants les espèces, précisément la moyenne des carrés des distances entre les espèces et leur centre de gravité (les probabilités \(\mathbf{p}\) des espèces constituent leur poids), est alors égale à l’entropie de Rao \(H_{\mathbf{\Delta}}\left(\mathbf{p}\right)\), où la matrice de distances \(\mathbf{\Delta}\) est \({\mathbf{D}^{\circ2}}/{2}\) : les valeurs de \(\mathbf{\Delta}\) valent la moitié du carré de celles de \(\mathbf{D}\). Cette représentation est étendue dans la double analyse en composantes principales de Pavoine, Dufour, et Chessel (2004), section 12.5.

Dans ADE4, les arbres phylogénétiques sont donc stockés sous la forme d’objets de type phylog où la matrice des distances (\$Wdist) est \(\mathbf{D}\) mais les longueurs des branches de l’arbre (\$droot) correspondent aux valeurs de \(\mathbf{\Delta}\).

library("ade4")
divc(as.data.frame(Ps), Paracou618.Taxonomy$Wdist)

##    diversity
## Ps 0.9854485

divc peut traiter plusieurs communautés simultanément ; Rao peut être utilisé avec la fonction apply :

divc(as.data.frame(Paracou618.MC$Psi), Paracou618.Taxonomy$Wdist)

##      diversity
## P006 0.9727197
## P018 0.9794563

apply(Paracou618.MC$Psi, 2, Rao, Tree = Paracou618.Taxonomy)

##     P006     P018 
## 2.820856 2.876405

7.6.5 Maximum théorique

Pavoine, Ollier, et Dufour (2005) ont défini l’originalité d’une espèce comme sa fréquence maximisant l’entropie quadratique, sachant la matrice de distances entre espèces. Les espèces les plus originales sont celles ayant le moins d’espèces proches dans la classification.

L’originalité n’est pas intéressante dans une taxonomie : une phylogénie doit être créée pour illustrer cette notion. Le fichier rao.traits.csv contient une espèce par ligne, identifiée par le champ Code, et un certain nombre de valeurs de traits en colonnes.

# Lecture des données: traits pour 34 espèces
read.csv2("data/rao.traits.csv", row.names = 1, header = T) ->
    traits

Le résultat est un data frame nommé traits à 8 lignes (espèces) et 6 colonnes (traits) :

# Aperçu
traits[1:4, 1:3]

##          SLA       Am       Gm
## Ess 10.10341 97.88627 1.454455
## Me  14.27473 63.52255 1.493502
## S1  13.71211 73.57748 1.963457
## Sr  10.71081 68.03988 1.305796

La matrice de distances est créée par classification automatique hiérarchique.

# ACP sur les traits foliaires
pcaf <- dudi.pca(traits, scale = T, scannf = FALSE, nf = 2)

Figure 7.8: Analyse en composante principale des traits foliaires

pcaf (figure 7.8) est une liste qui contient les résultats de l’ACP, à utiliser pour la classification :

# CAH Ward des traits foliaires
hf <- hclust(dist(pcaf$tab), "ward.D")

Code R pour la figure 7.8 :

scatter(pcaf)

Figure 7.9: Arbre phylogénétique issu de la classification automatique.

Le résultat de la classification est un objet hclust (figure 7.9 qui doit être transformé en phylog pour la suite de l’analyse :

# Transformation de l'arbre du format hclust au format
# phylog
phyf <- hclust2phylog(hf)

Code R pour la figure 7.9 :

plot(hf, h = -1)

Le résultat est en figure 7.10.

Figure 7.10: Présentation de l’arbre phylogénétique avec la contribution de chacune des variables.

Code R pour la figure 7.10 :

table.phylog(pcaf$tab[names(phyf$leaves), ], phyf)

La limite des distances ultramétriques est leur tendance à déformer le jeu de points (Pavoine, Ollier, et Dufour 2005). Dans cet exemple, les deux premiers axes de l’ACP rendent compte de presque toute l’inertie. Le nuage de points est pratiquement contenu dans un plan alors que sa représentation en distance ultramétrique est une hypersphère en 7 dimensions.

Le calcul de l’originalité des espèces utilise la fonction originality (figure 7.11).

Figure 7.11: Originalité des espèces.

Code R pour la figure 7.11 :

dotchart.phylog(phyf, originality(phyf, 5))

La fonction a pour paramètres l’objet phylog contenant la classification et le numéro de la méthode de calcul à utiliser, 5 pour l’entropie quadratique. Sa représentation graphique est faite par dotchart.phylog :

L’originalité ne repose que sur l’arbre, pas sur la fréquence des espèces.

Si la distance utilisée n’est pas ultramétrique, il existe plusieurs distributions possibles d’espèces qui maximisent la diversité (Pavoine et Bonsall 2009), le concept d’originalité n’a pas de sens dans ce cas.

La valeur de l’entropie quadratique dépend de la hauteur de l’arbre. Plusieurs normalisations ont été proposées : par sa valeur maximale ou par la diversité de Simpson (correspondant à un arbre dont toutes les espèces seraient équidistantes) (Ricotta et Avena 2005), ou en fixant la hauteur de l’arbre à 1 (Marcon et Hérault 2015a).

7.7 Diversité et moyenne

Garnier et al. (2004) définissent la moyenne pondérée d’un trait à l’échelle de la communauté (CWM : Community Weigthed Mean), simplement égal à la moyenne de la valeur du trait pondérée par la fréquence des espèces :

\[\begin{equation} \tag{7.21} \mathit{CWM} = \sum_s{p_s y_s}. \end{equation}\]

CWM n’est pas une mesure de diversité fonctionnelle, bien qu’il ait été utilisé parfois en tant que tel (Lavorel et al. 2008), mais une mesure de la composition de la communauté. CWM peut être étendu à plusieurs traits : le vecteur formé par les valeurs de CWM pour chaque trait correspond au centre de gravité de la communauté représentée dans l’espace des traits. L’entropie quadratique de Rao mesure la dispersion des espèces autour de ce point : les deux mesures se complètent donc (Ricotta et Moretti 2011).

7.8 Variations sur l’entropie quadratique

Izsák et Pavoine (2011) proposent deux variantes de l’indice de Rao dans lesquelles la distance entre espèces dépend de leurs probabilités :

\[\begin{equation} \tag{7.22} L_1 = \sum_{s}{\sum_{t}{p_{s}p_{t}{\left(p_{s}-p_{t}\right)}^2}}; \end{equation}\]

\[\begin{equation} \tag{7.23} L_2=\sum_{s}{\sum_{t}{p_{s}p_{t}{\left(\ln{p_{s}}-\ln{p_{t}}\right)}^2}}. \end{equation}\]

Ces indices sont proposés pour leurs propriétés mathématiques, assurant l’existence de sa décomposition, sans support écologique bien établi.

\(\mathbf{\Delta}\) est la matrice de dissimilarité dont les éléments sont \(\delta_{s,t}\), la dissimilarité entre l’espèce \(s\) et l’espèce \(t\). R. C. Guiasu et S. Guiasu (2011, 2012) proposent l’indice \(\mathit{{GS}_{D}}\) pour ses propriétés mathématiques et fournissent sa décomposition :

\[\begin{equation} \tag{7.24} \mathit{{GS}_{D}}=\sum_{s}{\sum_{t}{\delta_{s,t}p_{s}}}p_{t}\left(1-p_{s}p_{t}\right). \end{equation}\]

7.9 Diversité fonctionnelle de Chiu et Chao

Chiu et Chao (2014) proposent de pondérer l’entropie quadratique par la distance entre les paires d’espèces et obtiennent un nombre de Hill permettant de mesurer la diversité fonctionnelle à partir d’une matrice de dissimilarité :

\[\begin{equation} \tag{7.25} ^{q}\!D\left(Q\right) = \left[\sum_s{\sum_t{\frac{\delta_{s,t}}{Q}\left(p_s p_t\right)^q}}\right]^\frac{1}{2\left(1-q\right)}; \end{equation}\]

\[\begin{equation} \tag{7.26} ^{1}\!D\left(Q\right) = e^{\frac{1}{2}\left[\sum_s{\sum_t{p_s p_t\frac{\delta_{s,t}}{Q}\ln{p_s p_t}}}\right]}. \end{equation}\]

La notation \(^{q}\!D(Q)\) fait référence à l’entropie quadratique \(Q = {^{2}\!\bar{H}}(T)\). Une approche complémentaire est développée ci-dessous. Chiu et Chao notent que \(\mathit{{GS}_{D}} = Q - ^{q}\!D(Q)\).

La définition de Chiu et Chao revient à calculer l’entropie des paires d’individus à partir de la fonction d’information \[I(p_s p_t) = \ln_q[\frac{(\frac{\delta_{s,t}}{Q})^{\frac{1}{1-q}}}{p_s p_t}]\] pour \(q \ne 1\) et \[I(p_s p_t) = \ln[\frac{1}{(p_s p_t)^{\frac{\delta_{s,t}}{Q}}}]\] pour \(q=1\). Le nombre effectif de paires est \([^{q}\!D(Q)]^2\). Le nombre effectif d’espèces est donc \(^{q}\!D(Q)\).

Le nombre effectif de paires est le nombres de paires équifréquentes dont la distance entre les deux espèces est \(Q\). Le problème de cette approche est que les paires constituées de la même espèce doivent aussi avoir une distance \(\delta_{s,s}\) égale à \(Q\). Chiu et Chao considèrent ce point comme la possibilité de prendre en compte la variabilité intraspécifique, mais elle doit être identique à la variabilité interspécifique, ce qui n’est pas très convaincant. En absence de variabilité intraspécifique, Chiu et Chao redéfinissent la distance de référence : \(\delta_{s,s}=0\) et \(\delta_{s,t}=(\frac{D}{D-1})Q\). Il n’est donc pas possible de comparer le nombre effectif d’espèces de deux communautés différentes puisque la définition même du nombre effectif dépend de la diversité, ce qui invalide cette définition de la diversité fonctionnelle.

Enfin, cette définition de la diversité ne respecte pas le principe de Solow, Polasky, et Broadus (1993) selon lequel le remplacement d’une partie des effectifs d’une espèce par le même nombre d’individus d’une espèce différente mais fonctionnellement identique ne doit pas faire varier la diversité (Botta-Dukát 2018).

7.10 \(H_p\) et \(I_1\)

Simultanément, Pavoine, Love, et Bonsall (2009) et Allen, Kon, et Bar-Yam (2009) ont proposé la généralisation de l’indice de Shannon à la diversité phylogénétique. La présentation de Allen et al. est donnée ici, celle de Pavoine et al., plus générale, sera détaillée dans le paragraphe suivant.

Figure 7.12: Arbre phylogénétique ou fonctionnel hypothétique.

Étant donné une phylogénie, comme celle de la figure 7.12, on définit une branche \(b_{k,l}\) comme un segment terminé par une feuille (au bas de l’arbre) ou un noeud (dans l’arbre). \(k\) indique la période de l’arbre à laquelle la branche se termine, \(l\) le numéro d’ordre. Une branche n’existe que si elle se termine effectivement par un noeud ou une feuille : il n’y a pas de branche \(b_{2,1}\) par exemple. Sa probabilité \(p(b_{k,l})\) est la somme des probabilités des feuilles de la branche, c’est-à-dire \(u_{k,l}\), et \(l(b)\) est sa longueur. Sur la figure, la branche commençant en haut de l’arbre et se terminant au noeud réunissant les espèces 3 à 5 a une valeur \(p(b_{2,3})\) égale à la somme des probabilités d’occurrence des espèces 3 à 5 alors que \(p(b_{1,1})\) est seulement la probabilité de l’espèce 1. Leurs longueurs respectives sont \(T_2+T_3\) et \(T_1+T_2\). L’arbre possède 7 branches.

L’indice d’entropie phylogénétique est

\[\begin{equation} \tag{7.27} H_p =-\sum_{b}{l(b)p(b)\ln{p}(b)}. \end{equation}\]

Dans un arbre parfaitement régulier, toutes les branches sont de longueur 1 et \(H_p\) est l’indice de Shannon.