8 Entropie phylogénétique
L’entropie phylogénétique est la moyenne de l’entropie HCDT le long d’un arbre phylogénétique. Son estimation est simplement celle de l’entropie HCDT à chaque période de l’arbre. Elle va de pair avec la diversité phylogénétique qui est son nombre effectif d’espèces, c’est-à-dire le nombre d’espèces équiprobables, dans un arbre où toutes les espèces descendraient d’un ancêtre unique, dont l’entropie serait la même que celle de la communauté réelle. Dans un tel arbre, la diversité phylogénétique se réduit à la diversité neutre.
L’entropie HCDT peut être étendue pour définir une mesure de diversité prenant en compte l’histoire évolutive des espèces.
8.1 Généralisation de l’entropie HCDT
Pavoine et Bonsall (2009) découpent l’arbre phylogénétique en périodes. À partir de la racine de l’arbre, une nouvelle période est définie à chaque ramification d’une branche quelconque. Les débuts et fins de périodes sont notés \(t_k\), la racine de l’arbre est fixée à \(t_0=0\). L’arbre est ultramétrique.
Nous suivrons plutôt les notations de Chao, Chiu, et Jost (2010) en numérotant les périodes à partir du présent et en notant \(T_k\) leur durée. Figure 7.7, la première période se termine quand les branches des espèces 3 à 5 se rejoignent. L’arbre comprend \(K=3\) périodes.
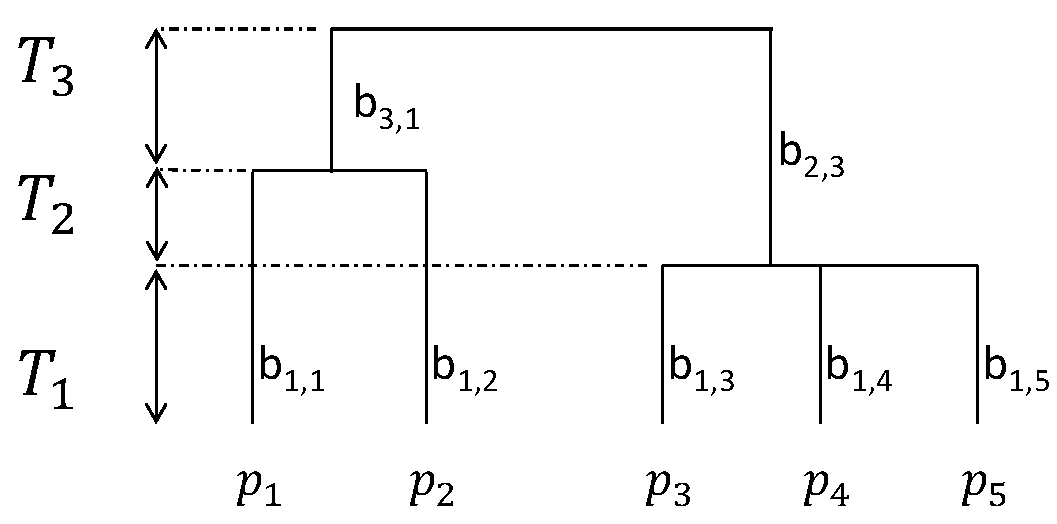
Figure 8.1: Arbre phylogénétique ou fonctionnel hypothétique. 5 espèces sont présentes (\(S=5\)), leurs probabilités notées \(p_1\) à \(p_5\). Les noms des branches sont affichés.
L’entropie HCDT (\(^{q}\!H\) de l’équation (4.5)) est calculée à chaque période. Figure 8.1, à la deuxième période (\(T_2\)), l’arbre a trois feuilles, avec des probabilités égales à celle des espèces 1 et 2 et la somme de celles des espèces 3 à 5. \(^{q}\!H\) peut être calculée avec ces valeurs de probabilités. On notera cette valeur d’entropie \(^{q}_{k}\!H\) où \(k\) est le quantième de la période.
L’indice \(I_q\) de Pavoine et al. est la somme des \(^{q}_{k}\!H\) pondérée par la durée de chaque période. Nous le normalisons par la hauteur totale de l’arbre (\(T\)) pour définir \(^{q}\!\bar{H}(T)\) :
\[\begin{equation} \tag{8.1} ^{q}\!\bar{H} \left( T \right)=\sum_{k=1}^K{\frac{T_k}{T}^{q}_{k}\!H}. \end{equation}\]
Dans un arbre parfaitement régulier, toutes les branches sont de longueur 1, il n’y a qu’une seule période, et \(I_q={^{q}\!H}\).
Shimatani (2001a) puis Ricotta (2005b) avaient montré que l’indice de Rao est la somme pondérée sur chaque période de l’indice de Simpson, c’est-à-dire l’égalité (8.1) pour le cas particulier \(q=2\).
Les indices \(^{q}\!\bar{H}(T)\) généralisent les mesures d’entropie classique à la diversité phylogénétique : \(T[^{0}\!\bar{H}(T)+1]\) est égal à PD ou FD, \(^{1}\!\bar{H}(T)\) est \(H_p\) et \(^2{\bar{H}(T)}\) est l’indice de Rao. On peut les interpréter intuitivement comme une somme pondérée par la longueur des périodes des valeurs de l’entropie à chaque période. À la dernière période (près des feuilles), toutes les classes sont présentes, la diversité est donc maximale. En remontant dans l’arbre, les classes se confondent et la diversité diminue progressivement. Deux classes peu distantes, comme les espèces 3 à 5 de la figure 8.1, apportent peu de diversité supplémentaire par rapport à une situation où les deux espèces seraient confondues (et leurs effectifs ajoutés), contrairement aux espèces 1 et 2.
8.2 Estimation
La correction du biais d’estimation applicable à l’entropie généralisée l’est aussi à chaque période de l’arbre. Les biais sont de moins en moins importants quand on se rapproche de la racine de l’arbre : il est de moins en moins probable de ne pas observer une classe quand les classes sont de plus en plus vastes.
Le package entropart fournit la fonction PhyloEntropy pour calculer \(^{q}\!\bar{H}(T)\) à partir d’un vecteur de probabilité ou d’abondances.
Dans le dernier cas, la correction de Tsallis est appliquée à chaque période.
Exemple : le package contient les données d’inventaire de deux hectares du dispositif de Paracou et la taxonomie des espèces concernées. Le calcul de l’indice de Rao, corrigé du biais d’estimation utilise le code suivant :
data(Paracou618)
PhyloEntropy(Paracou618.MC$Ns, 2, Paracou618.Taxonomy)## $Distribution
## [1] "Paracou618.MC$Ns"
##
## $Function
## [1] "PhyloEntropy"
##
## $Tree
## [1] "Paracou618.Taxonomy"
##
## $Normalized
## [1] TRUE
##
## $Cuts
## 1 2 3
## 0.9863189 0.9709766 0.9232516
##
## $Corrections
## 1 2 3
## "UnveilJ" "UnveilJ" "UnveilJ"
##
## $Total
## [1] 0.9601824
##
## $Type
## [1] "alpha or gamma"
##
## $Order
## [1] 2
##
## $Correction
## [1] "Best"
##
## attr(,"class")
## [1] "PhyloEntropy" "PhyloValue"La fonction retourne la valeur de \(^{q}_{k}\!H\) dans chaque intervalle (l’arbre est ici une taxonomie espèce-genre-famille, correspondant aux limites des périodes (Cuts) 1, 2 et 3 dont l’entropie va en décroissant) et la valeur de \(^{q}\!\bar{H}(T)\).
8.3 Entropie et diversité
La diversité phylogénétique est le nombre d’espèces équifréquentes et dont la distance à toutes les autres dans la phylogénie est maximale, dont l’entropie serait égale à l’entropie observée.
La possibilité de choisir comme distance de référence entre espèces une valeur inférieure à la distance maximale est discutée par Ricotta et Acosta (2014) pour la diversité fonctionnelle : sa signification biologique est liée à l’espace fonctionnel disponible pour la communauté, qui peut être trop réduit pour permettre la coexistence d’espèces dont la dissimilarité serait maximale.
L’entropie \(^{q}\!\bar{H}(T)\) peut être transformée en diversité (Marcon et al. 2014) de la même façon que \(^{q}\!D = e^{^{q}\!H}\) :
\[\begin{equation} \tag{8.2} ^{q}\!\bar{D}\left(T\right)=e^{^{q}\!\bar{H}\left(T\right)}_q. \end{equation}\]
Le nombre effectif d’espèces de l’entropie de Rao, \({^{2}\!\bar{D}}(T)=\frac{1}{[1-{^{2}\!\bar{H}}(T)]}\) a été établi par Ricotta et Szeidl (2009).
Chao, Chiu, et Jost (2010) obtiennent ce résultat sans recourir explicitement à l’entropie, mais en faisant le même calcul :
\[\begin{equation} \tag{8.3} {^{q}\!\bar{D}} \left( T \right) =\left( \sum_b{\frac{l(b)}{T} p(b)^q} \right)^{\frac{1}{1-q}}. \end{equation}\]
La somme est sur l’ensemble des branches de l’arbre, défini de façon identique à celle de Allen, Kon, et Bar-Yam (2009) 7.10.
Les entropies ont un comportement linéaire : elles s’additionnent tout au long de l’arbre pour donner \(^{q}\!\bar{H}(T)\). Les diversités \(^{q}_{k}\!D\) calculées à chaque période ne peuvent pas être sommées sur le modèle de l’équation (8.1) : \(^{q}\!\bar{D}(T)\) n’est pas la moyenne pondérée des diversités aux différentes périodes, sauf dans le cas particulier \(q=1\) où, comme pour la décomposition de l’indice de Shannon, il en est la moyenne géométrique pondérée.
La fonction PhyloDiversity de entropart permet de calculer \(^{q}\!\bar{D}(T)\) avec ou sans correction de biais, selon qu’elle traite un vecteur d’abondances ou de probabilités.
À la suite de l’exemple précédent, les résultats sont présentés sous forme de diversité au lieu d’entropie :
PhyloDiversity(Paracou618.MC$Ns, 2, Paracou618.Taxonomy)## $Distribution
## [1] "Paracou618.MC$Ns"
##
## $Function
## [1] "bcPhyloDiversity"
##
## $Tree
## [1] "Paracou618.Taxonomy"
##
## $Normalized
## [1] TRUE
##
## $Cuts
## 1 2 3
## 73.09335 34.45501 13.02960
##
## $Corrections
## 1 2 3
## "UnveilJ" "UnveilJ" "UnveilJ"
##
## $Total
## [1] 25.11451
##
## $Type
## [1] "alpha or gamma"
##
## $Order
## [1] 2
##
## $Correction
## [1] "Best"
##
## attr(,"class")
## [1] "PhyloDiversity" "PhyloValue"8.4 Diversité individuelle
La construction de la diversité fonctionnelle ou phylogénétique n’implique pas de regrouper les individus par espèces : chaque catégorie peut se réduire à un individu si des données individuelles moléculaires ou de traits sont disponibles.
Le regroupement des individus en une espèce revient simplement à considérer leur distance comme nulle. Diviser une espèce en deux espèces infiniment proches revient seulement à créer une période supplémentaire dans l’arbre, de longueur infinitésimale ; en d’autres termes, la mesure de diversité est continue face au regroupement. Cette propriété permet de limiter les conséquences du problème de l’espèce : séparer les individus d’une espèce en deux espèces proches dans l’arbre n’a que peu d’effet sur la diversité.
8.5 Arbres non ultramétriques
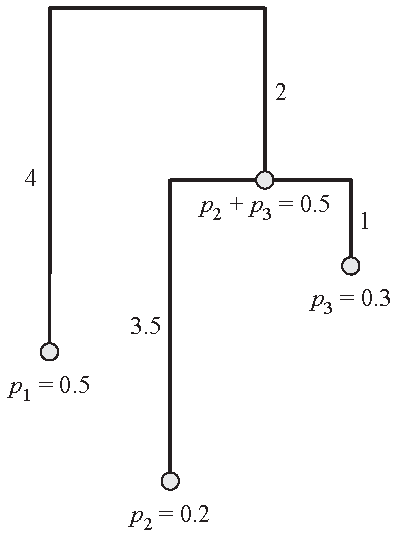
Figure 8.2: Arbre phylogénétique hypothétique non ultramétrique
Chao, Chiu, et Jost (2010) définissent la diversité phylogénétique selon l’équation (8.3) quelle que soit la forme de l’arbre, y compris s’il n’est pas ultramétrique. Dans ce cas, \(T\) est remplacé par \(\bar{T}\), la longueur moyenne des branches pondérée par la fréquence des espèces. Cette généralisation est très discutable : son sens n’est pas clair sur le plan de la mesure de la diversité au-delà du parallélisme de la forme mathématique.
L’arbre de la figure 8.2 (Chao, Chiu, et Jost 2010, fig. 1b) peut être découpé en périodes mais les deux premières (\(T_1\) : seule l’espèce 2 est présente ; \(T_2\) : les espèces 1 et 2 sont présentes) sont incomplètes au sens où la somme des probabilités n’y est pas égale à 1 donc \({\left(\sum{p^q_i}\right)}^{\frac{1}{1-q}}\) ne définit pas une diversité à ces périodes.
Pavoine et Bonsall (2009) traitent en détail les résultats aberrants que cause un arbre non ultramétrique dans le cas particulier de l’entropie de Rao. Leinster et Cobbold (2012) montrent qu’un arbre non ultramétrique implique que la dissimilarité entre les espèces dépende de leur fréquence, ce qui est contradictoire avec le cadre dans lequel la diversité phylogénétique a été définie.
Dans l’état actuel des connaissances, aucune méthode n’est applicable de façon satisfaisante aux arbres non ultramétriques.