9 Diversité de Leinster et Cobbold

La diversité de Leinster et Cobbold est l’inverse de la banalité moyenne des espèces, qui est elle-même la similarité moyenne d’une espèce aux autres. Elle va de pair avec l’entropie de Ricotta et Szeidl, dont la fonction d’information est le logarithme déformé de l’inverse la banalité. La diversité peut être calculée directement à partir de la distance entre espèces, sans recourir à un dendrogramme intermédiaire qui déformerait la topologie des espèces.

À partir de la théorie mathématique des catégories (Leinster 2013), Leinster et Cobbold (2012) ont proposé une mesure de diversité applicable à une communauté dont la position des espèces dans un espace multidimensionnel euclidien est connue. C’est donc une mesure applicable à la diversité fonctionnelle.

9.1 Définitions

Leinster et Cobbold (2012) proposent une unification des mesures de diversité à partir de la définition de la banalité des espèces. Une matrice carrée de dimension égale au nombre d’espèces, \(\mathbf{Z}\), décrit par ses valeurs \(z_{s,t}\) la similarité entre l’espèce \(s\) et l’espèce \(t\) comprises entre 0 et 1 (\(z_{s,s}=1\)).

La banalité d’une espèce \(s\) est définie par \(\sum_t{p_t z_{s,t}}\), c’est-à-dire la moyenne pondérée de sa similarité avec toutes les autres espèces : au minimum \(p_s\) si elle est totalement différente des autres (approche de la diversité neutre, \(\mathbf{Z}\) est la matrice identité \(\mathbf{I}_s\)), au maximum 1 si toutes les espèces sont totalement similaires (\(\mathbf{Z}\) ne contient que des 1). Une espèce rare totalement différente des autres est peu banale.

La moyenne généralisée d’ordre \(r\) (G. H. Hardy, Littlewood, et Pólya 1952), generalized mean ou power mean en anglais, est définie pour une distribution de valeurs de \(x_s\) dont la probabilité d’occurrence est \(p_s\) par

\[\begin{equation} \tag{9.1} \bar{x}={\left(\sum_s{p_s x^r_s}\right)}^{\frac{1}{r}}. \end{equation}\]

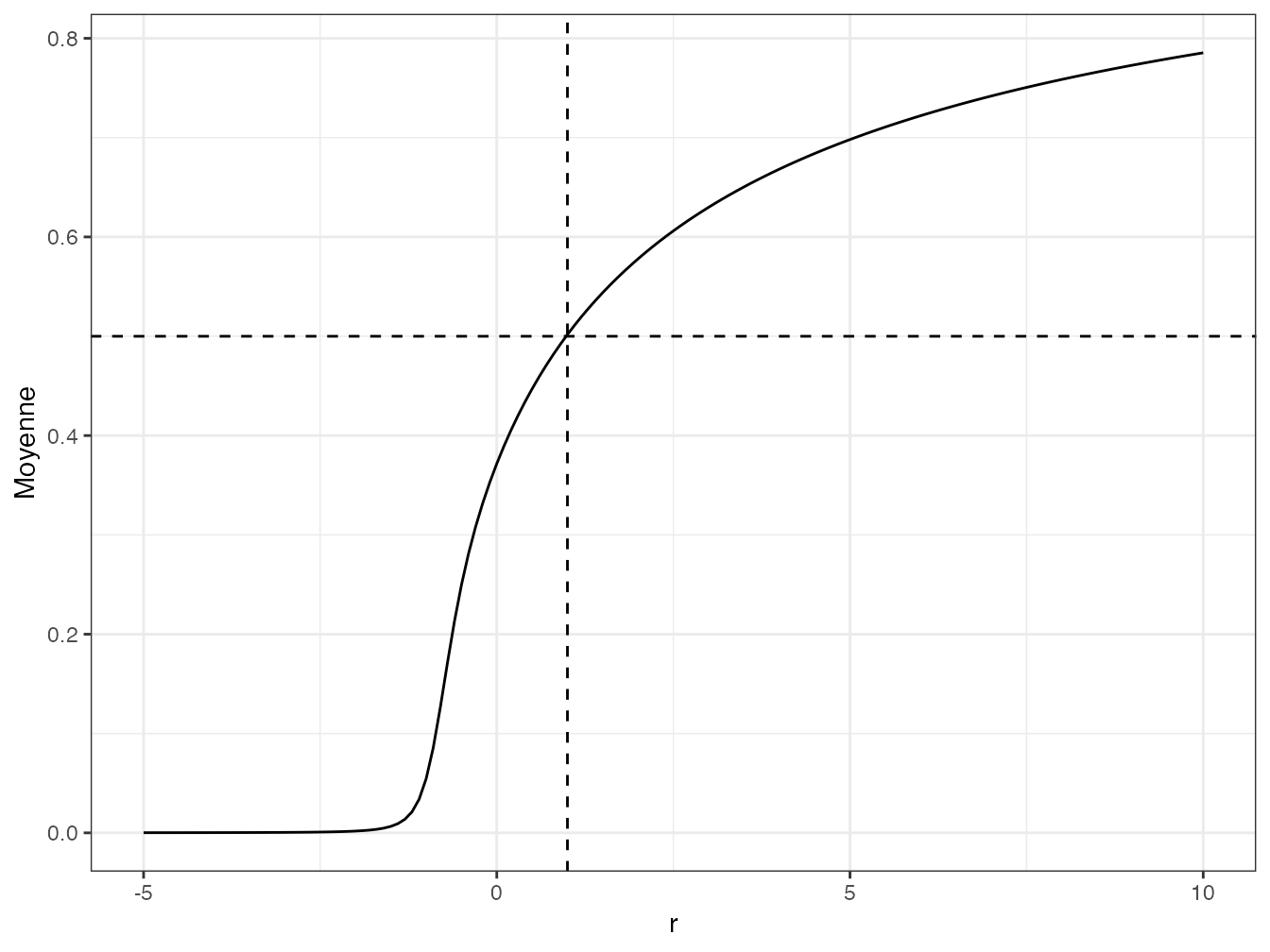
Figure 9.1: Moyenne généralisée d’ordre \(r\) (en abscisse) d’une distribution uniforme de 10000 valeurs tirées entre 0 et 1. La moyenne arithmétique 0,5 est obtenue pour \(r=1\). La moyenne généralisée tend vers la plus petite valeur (près de 0) quand \(r\to -\infty\), et vers la plus grande valeur (près de 1) quand \(r\to +\infty\).

La moyenne généralisée se réduit à la moyenne arithmétique pondérée pour \(r=1\). Elle donne un fort poids aux petites valeurs de \(x_s\) dans la moyenne pour les faibles valeurs de \(r\) (qui peuvent être négatives), et un fort poids aux grandes valeurs quand \(r\) est grand (figure 9.1).

Le code R nécessaire pour réaliser la figure est :

X <- runif(10000)
# La moyenne n'est pas définie à r=0, décalage de 10^-8
r <- seq(-5, 10, .1) + 1E-8
# Préparation des données
df <- data.frame(r, Moyenne = sapply(r, function(r) (mean(X^r))^(1/r)))
ggplot(df, aes(x = r, y = Moyenne)) +
  geom_line() +
  geom_hline(yintercept = .5, lty = 2) +
  geom_vline(xintercept = 1, lty = 2)

La banalité peut s’écrire sous forme matricielle en notant \(\mathbf{p}\) le vecteur des probabilités \(p_s\), on note alors \({\left(\mathbf{Zp}\right)}_s=\sum_t{p_{t}z_{s,t}}\).

La banalité moyenne des espèces de la communauté est calculée en prenant \(r=q-1\) :

\[\begin{equation} \tag{9.2} \left(\overline{{\mathbf{Zp}}}\right) = {\left(\sum_s{p_s{\left(\mathbf{Zp}\right)}^{q-1}_s}\right)}^{\frac{1}{q-1}}. \end{equation}\]

La diversité de la communauté est simplement l’inverse de la banalité moyenne des espèces :

\[\begin{equation} \tag{9.3} ^q\!D^{\mathbf{Z}}={\left(\sum_s{p_s{\left(\mathbf{Zp}\right)}^{q-1}_s}\right)}^{\frac{1}{1-q}}. \end{equation}\]

\(^q\!D^{\mathbf{Z}}\) converge vers \(^1\!D^{\mathbf{Z}}\) quand \(q\) tend vers 1 :

\[\begin{equation} \tag{9.4} ^1\!D^{\mathbf{Z}} = \frac{1}{\prod_s{{\left(\mathbf{Zp}\right)}^{p_s}_s}}. \end{equation}\]

9.2 Diversité neutre

Leinster et Cobbold montrent que la diversité HCDT est un cas particulier de \(^q\!D^{\mathbf{Z}}\), pour la matrice identité :

\[\begin{equation} \tag{9.5} ^{q}\!D={^q\!D^{\mathbf{I}}}. \end{equation}\]

9.3 Diversité non neutre

Une mesure de diversité non neutre est obtenue en utilisant une matrice \(\mathbf{Z}\) qui contient l’information sur la similarité entre les espèces. La dissimilarité entre espèces peut être obtenue à partir des arbres. L’exemple suivant utilise les données du calcul d’originalité, section 7.6.5. Pour un arbre de classe hclust, la fonction cophenetic fournit une demi-matrice de distances (classe dist).

print(cophenetic(hf), digits = 4)

##      Ess    Me    S1    Sr    Vm    Bg    Ef
## Me 1.224                                    
## S1 1.224 1.003                              
## Sr 2.464 2.464 2.464                        
## Vm 9.731 9.731 9.731 9.731                  
## Bg 9.731 9.731 9.731 9.731 5.653            
## Ef 9.731 9.731 9.731 9.731 1.694 5.653      
## Dg 9.731 9.731 9.731 9.731 1.101 5.653 1.694

La matrice doit être normalisée puis transformée en matrice de similarité. Une transformation simple est 1 moins la dissimilarité (préalablement normalisée pour être comprise entre 0 et 1) :

Dis <- cophenetic(hf)
print((Z <- 1 - as.matrix(Dis/max(Dis))), digits = 4)

##        Ess     Me     S1     Sr     Vm     Bg     Ef     Dg
## Ess 1.0000 0.8742 0.8742 0.7468 0.0000 0.0000 0.0000 0.0000
## Me  0.8742 1.0000 0.8969 0.7468 0.0000 0.0000 0.0000 0.0000
## S1  0.8742 0.8969 1.0000 0.7468 0.0000 0.0000 0.0000 0.0000
## Sr  0.7468 0.7468 0.7468 1.0000 0.0000 0.0000 0.0000 0.0000
## Vm  0.0000 0.0000 0.0000 0.0000 1.0000 0.4191 0.8259 0.8868
## Bg  0.0000 0.0000 0.0000 0.0000 0.4191 1.0000 0.4191 0.4191
## Ef  0.0000 0.0000 0.0000 0.0000 0.8259 0.4191 1.0000 0.8259
## Dg  0.0000 0.0000 0.0000 0.0000 0.8868 0.4191 0.8259 1.0000

La diversité peut être calculée par la fonction Dqz de entropart :

# Vecteur contenant 8 espèces...
(read.csv2("data/rao.effectifs.csv", row.names = 1, header = T) ->
    effectifs)

##     P1 P2 P3 P4
## Ess 97 36 34 61
## Me  62 24 49  4
## S1   4  6  6 75
## Sr  71 78 99 36
## Vm  76 29 34  2
## Bg  58 49 47 19
## Ef   9 34 91 35
## Dg  98 14 95 14

Ps <- rowSums(effectifs)/sum(effectifs)
Dqz(Ps, q = 2, Z)

##     None 
## 2.520938

Dans le cas particulier \(q=2\), \(^2\!D^{\mathbf{Z}}\) est égal à \(^{2}\!\bar{D}(T)\) :

PhyloDiversity(Ps, q = 2, phyf)$Total

##     None 
## 2.520938

Mais ce n’est pas le cas en général.

9.4 Entropie de Ricotta et Szeidl

Ricotta et Szeidl (2006) ont montré une similitude entre les entropies de Shannon et de Rao en généralisant l’entropie de Shannon en deux temps. Tout d’abord en remarquant que la probabilité d’occurrence d’une espèce est 1 moins la somme de celle des autres, d’où

\[\begin{equation} \tag{9.6} ^{1}\!H = -\sum_s{p_s\ln\left(1-\sum_{t\ne s}{p_t}\right)}. \end{equation}\]

\(1-\sum_{t\ne s}{p_t}\) est la banalité de l’espèce \(s\) si on mesure la diversité neutre. De façon plus générale, \({(\mathbf{Zp})}_s\) peut exprimer cette banalité. Enfin, l’entropie HCDT peut généraliser l’entropie de Shannon pour définir une mesure \(Q_{\alpha}\) que nous noterons \(^q\!H^{\mathbf{Z}}\) pour la cohérence de nos notations (\(q=\alpha\)) :

\[\begin{equation} \tag{9.7} ^q\!H^{\mathbf{Z}} = \sum_s{p_{s}\ln_q{\frac{1}{\left(\mathbf{Zp}\right)_s}}}. \end{equation}\]

De façon plus rigoureuse, on peut remarquer que \({(\mathbf{Zp})}_s\) décroît quand \(p_s\) décroît parce que la similarité d’une espèce avec elle-même est maximale. Une entropie définie à partir d’une fonction d’information de \(p_s\) reste donc une entropie quand on utilise la même fonction d’information sur \({(\mathbf{Zp})}_s\) : la fonction reste décroissante et vaut 0 pour \(p_s=1\) puisque \({(\mathbf{Zp})}_s=1\) dans ce cas. \(^q\!H^{\mathbf{Z}}\) est donc bien une entropie. La fonction d’information \(\ln_q(1/p_s)\) de l’entropie HCDT (4.16) est simplement remplacée par \(\ln_q(1/{(\mathbf{Zp})}_s)\).

L’entropie de Ricotta et Szeidl étend l’entropie HCDT en utilisant une fonction d’information plus générale, dépendant de la banalité de l’espèce plutôt que de sa seule probabilité, les deux étant égales dans le cas particulier de la diversité neutre. L’ordre de la diversité \(q\) permet de donner un plus ou moins grand poids aux espèces banales (et non aux espèces fréquentes : \(p_s\) est à la puissance 1). La fréquence et la banalité se confondent seulement pour la diversité neutre.

Le logarithme d’ordre \(q\) de \(^q\!D^{\mathbf{Z}}\) est \(^q\!H^{\mathbf{Z}}\) :

\[\begin{equation} \tag{9.8} \ln_q{^q\!D^{\mathbf{Z}}} = ^q\!H^{\mathbf{Z}}. \end{equation}\]

9.5 Définition de la similarité

La transformation d’une matrice de dissimilarité en une matrice de similarité nécessite une fonction strictement décroissante, dont le résultat est compris entre 0 et 1. La plus simple est \[z_{s,t} = 1 - \frac{d_{s,t}}{\max{(d_{s,t})}}.\] Leinster et Cobbold argumentent en faveur d’une transformation exponentielle négative, déjà utilisée par Nei (1972).

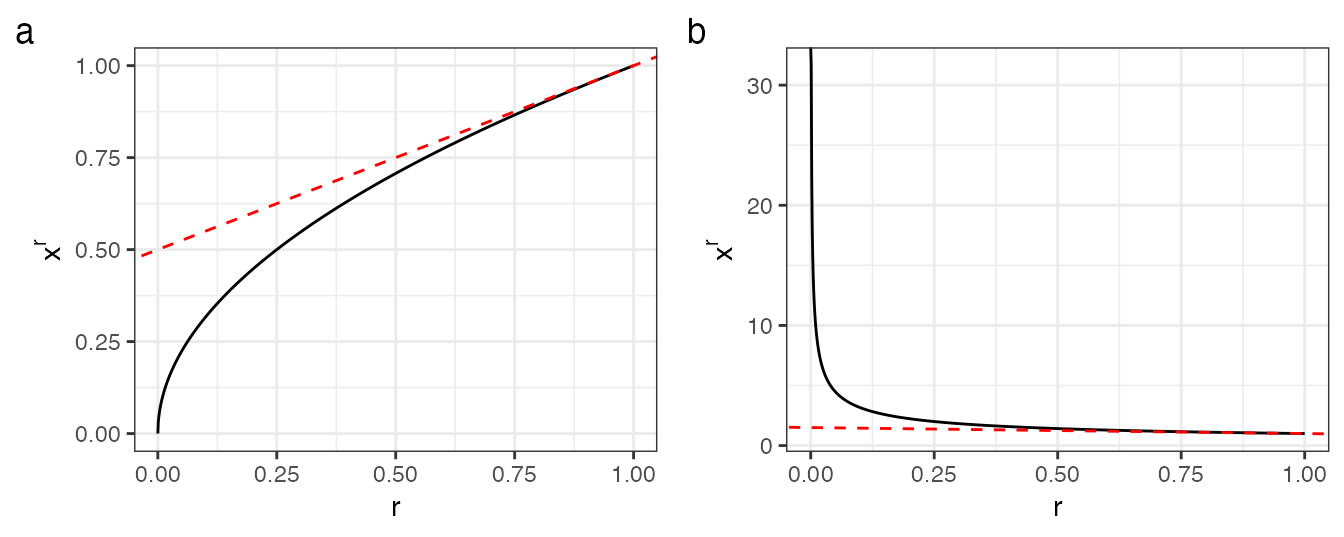
Figure 9.2: Approximation de \({(\mathbf{Zp})}_{s}^{q-1}\) par son développement limité au premier ordre pour (a) \(q=1.5\) (\(r=q-1\)) et (b) \(q=0.5\)

Le problème majeur de la diversité \(^q\!D^{\mathbf{Z}}\) est qu’elle fournit souvent des valeurs presque indépendantes de \(q\) quand on l’applique à une matrice de similarité fonctionnelle (Chiu et Chao 2014). De nombreux exemples, y compris dans l’article original de Leinster et Cobbold, montrent une très faible décroissance de la diversité de \(q=0\) à \(q=2\). Ce n’est pas un problème théorique mais numérique. Si la banalité de l’espèce \(s\) est proche de 1, sa puissance \(q\) peut être approchée par son développement limité au premier ordre : \[{(\mathbf{Zp})}_{s}^{q-1} \approx 1 + (q-1)[{(\mathbf{Zp})}_{s} - 1].\] Cette approximation linéaire implique que \[\sum_s{p_s{\left(\mathbf{Zp}\right)}^{q-1}_s} \approx [\sum_s{p_s{\left(\mathbf{Zp}\right)}_s}]^{q-1}.\] La puissance \(q-1\) disparaît donc dans le calcul de la diversité et l’équation (9.3) devient \[^q\!D^{\mathbf{Z}} \approx \bar{z}\] où \(\bar{z} = \sum_s{p_s (\mathbf{Zp})_s}\). Dans les faits, cette approximation vaut pour des valeurs de banalité assez éloignées de 1 (Figure 9.2).

Si une majorité des espèces (au sens de la somme de leurs probabilités respectives) a une banalité supérieure à 0,5, l’approximation linéaire est assez bonne et la moyenne généralisée de la banalité est proche de sa moyenne arithmétique. Ce n’est pas un problème pour la comparaison de profils de diversité de communautés différentes calculés à partir de la même matrice de similarité mais l’interprétation de la diversité en termes de nombres effectifs d’espèces dépendant de \(q\) n’est pas très intuitive.

Le code R nécessaire pour réaliser la figure est :

r <- 0.5
seqZp <- seq(0, 1, 0.001)
gga <- ggplot(data.frame(r = seqZp, xr = seqZp^r), aes(r, xr)) +
    geom_line() + geom_abline(intercept = 1 - r, slope = r, col = "red",
    lty = 2) + labs(y = expression(x^r)) + labs(tag = "a")
r <- -0.5
ggb <- ggplot(data.frame(r = seqZp, xr = seqZp^r), aes(r, xr)) +
    geom_line() + geom_abline(intercept = 1 - r, slope = r, col = "red",
    lty = 2) + labs(y = expression(x^r)) + labs(tag = "b")
grid.arrange(gga, ggb, ncol = 2)

La transformation exponentielle négative, \[z_{s,t} = e^{-u \frac{d_{s,t}}{\max{(d_{s,t})}}},\] est justifiée par Leinster (2013). \(u\) est une constante positive. Plus \(u\) est grand, plus la transformation est convexe : les similarités sont tassées vers 0 (figure 9.3).

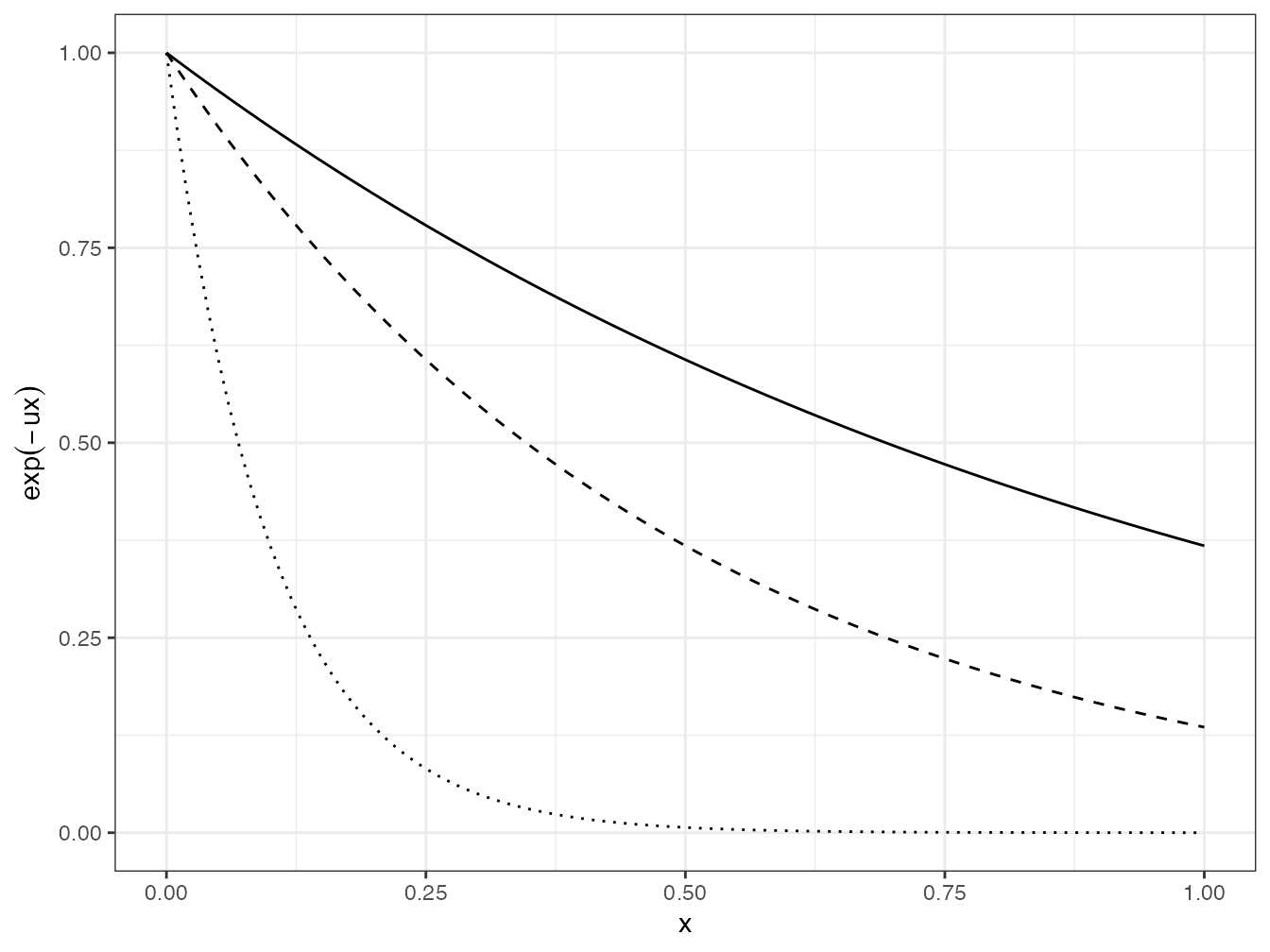
Figure 9.3: Transformation des distances (en abscisse) en similarités (en ordonnées) selon la valeur de \(u\). Trait plein : \(u=1\) ; pointillés longs : \(u=2\) ; pointillés : \(u=10\). Plus \(u\) est grand, plus les similarités sont tassées vers 0.

Le code R nécessaire pour réaliser la figure est :

ggplot(data.frame(x = seq(0, 1, by = .01)), aes(x)) + 
  stat_function(fun = function(x) exp(-x)) +
  stat_function(fun = function(x) exp(-2*x), lty = 2) +
  stat_function(fun = function(x) exp(-10*x), lty = 3) +
  labs(y = expression(exp(-ux)))

Augmenter la valeur de \(u\) diminue les similarités et donc la banalité des espèces, ce qui règle (arbitrairement) le problème de la faible sensibilité de la diversité au paramètre \(q\).

Du point de vue théorique, l’ordre des valeurs de la matrice des distances est justifié (par les différences entre traits fonctionnels par exemple) mais leur distribution ne l’est pas : elle n’est que la conséquence de la méthode de calcul. Le choix de \(u\) ne change pas l’ordre des distances mais déforme la distribution des similarités. La distance étant normalisée, \(u\) fixe l’échelle des distances avant la transformation.

Leinster relie la valeur de \(^q\!D^{\mathbf{Z}}\) à la magnitude de l’espace des espèces (espace dans lequel les espèces sont des points dont les distances deux à deux sont décrites par la matrice \(\Delta\), qui doit être euclidienne) : la magnitude de l’espace est la valeur maximale que peut atteindre la diversité. La magnitude est une propriété qui décrit la taille d’un espace dans le cadre de la théorie des catégories. Modifier \(u\) modifie la magnitude de l’espace selon une relation non triviale : \(u\) est un paramètre au même titre que \(q\). Quand \(u \to +\infty\), \(\mathbf{Z} \to \mathbf{I}_s\) : la diversité tend vers la diversité neutre. Leinster et Cobbold suggèrent de comparer les profils de diversité en fonction à la fois de \(q\) et de \(u\).

9.6 Estimation

Comme les autres mesures de diversité, \(^q\!D^{\mathbf{Z}}\) est sujette au biais d’estimation. Deux estimateurs réduisant le biais existent (Marcon, Zhang, et Hérault 2014). Le premier utilise la technique de Chao et Shen (2003) déjà vue pour la correction du biais de l’entropie de Shannon (3.37). L’estimateur de \(^q\!H^{\mathbf{Z}}\) est

\[\begin{equation} \tag{9.9} ^q\!{\tilde{H}}^{\mathbf{Z}} = \sum_s{\frac{\hat{C}\hat{p}_s \ln_q \frac{1}{{\left(\widetilde{\mathbf{Zp}}\right)}_s}}{1-{\left(1-\hat{C}\hat{p}_s\right)}^n}}, \end{equation}\]

où

\[\begin{equation} \tag{9.10} {\left(\widetilde{\mathbf{Zp}}\right)}_s = \sum_t{{\hat{C}\hat{p}}_t z_{s,t}} +\left(1-\hat{C}\right)\bar{z}. \end{equation}\]

L’estimateur de la diversité est \(^q\!{\tilde{D}}^{\mathbf{Z}} = e^{^q\!{\tilde{H}}^{\mathbf{Z}}}_q\).

L’autre estimateur suppose que la similarité des espèces non observées avec toutes les autres est la similarité moyenne observée. L’estimation utilise la technique de Z. Zhang et Grabchak (2016), qui consiste à développer l’estimateur en série entière au voisinage de \(p_s=1\). L’estimateur de \(^q\!D^{\mathbf{Z}}\) est, pour \(q\ne 1\),

\[\begin{equation} \tag{9.11} ^q\!{\tilde{D}}^{\mathbf{Z}} = {\left\{\hat{K}+\hat{V} -\sum_{s\le s_{\ne 0}}{\hat{C}\hat{p}_s{\left[\bar{z}\left(1-\hat{C}\hat{p}_s\right)+\hat{C}\hat{p}_s\right]}^{q-1}}\right\}} ^{\frac{1}{1-q}} \end{equation}\]

où

\[\begin{equation} \tag{9.12} \hat{K}=\sum_{s\le s_{\ne 0}}{\hat{C}\hat{p}_s{\left[\left(\sum_{t\le s_{\ne 0}}{\hat{C}\hat{p}_t z_{s,t}}\right)+\left(1-\hat{C}\right)\bar{z}\right]}^{q-1}} \end{equation}\]

et

\[\begin{equation} \tag{9.13} \hat{V}=1+\sum_{s\le s_{\ne 0}}{\frac{n_s}{n}\sum^{n-n_s}_{v=1}{{\left(1-\bar{z}\right)}^v\left[\prod^v_{i=1}{\frac{i-q}{i}}\right]\left[\prod^v_{j=1}{\left(1-\frac{n_s-1}{n-j}\right)}\right]}}. \end{equation}\]

L’estimateur de \(^q\!H^{\mathbf{Z}}\) est

\[\begin{equation} \tag{9.14} ^q\!{\tilde{H}}^{\mathbf{Z}} = \frac{\hat{K}+\hat{V}-\sum_{s\le s_{\ne 0}}{\hat{C}\hat{p}_s{\left[\bar{z}\left(1-\hat{C}\hat{p}_s\right)+\hat{C}\hat{p}_s\right]}^{q-1}}-1}{1-q}. \end{equation}\]

Pour \(q=1\),

\[\begin{equation} \tag{9.15} ^1\!{\tilde{H}}^{\mathbf{Z}} = \hat{L}+\hat{W}+\sum_{s\le s_{\ne 0}}{\hat{C}\hat{p}_s\ln\left[\bar{z}\left(1-\hat{C}\hat{p}_s\right)+\hat{C}\hat{p}_s\right]}, \end{equation}\] \[\begin{equation} ^1\!{\tilde{D}}^{\mathbf{Z}}=e^{^1\!{\tilde{H}}^{\mathbf{Z}}}, \end{equation}\]

où

\[\begin{equation} \tag{9.16} \hat{L}=-\sum_{s\le s_{\ne 0}}{\hat{C}\hat{p}_s \ln\left[\left(\sum_{t\le s_{\ne 0}}{{\hat{C}\hat{p}}_jz_{s,t}}\right)+\left(1-\hat{C}\right)\bar{z}\right]}, \end{equation}\] \[\begin{equation} \hat{W}=\sum_{s\le s_{\ne 0}}{\frac{n_s}{n}\sum^{n-n_s}_{v=1}{\frac{{\left(1-\bar{z}\right)}^v}{v}\left[\prod^v_{j=1}{\left(1-\frac{n_s-1}{n-j}\right)}\right]}}. \end{equation}\]

Le package entropart fournit les fonctions Dqz et HqZ pour calculer ces estimateurs.

data(Paracou618)
# Matrice de distances fonctionnelles
DistanceMatrix <- as.matrix(Paracou618.dist)
# Matrice de similarité
Z <- 1 - DistanceMatrix/max(DistanceMatrix)
# Calcul de la diversité
Dqz(Paracou618.MC$Ns, q = 1, Z)

##     Best 
## 1.488083

9.7 Diversité phylogénétique

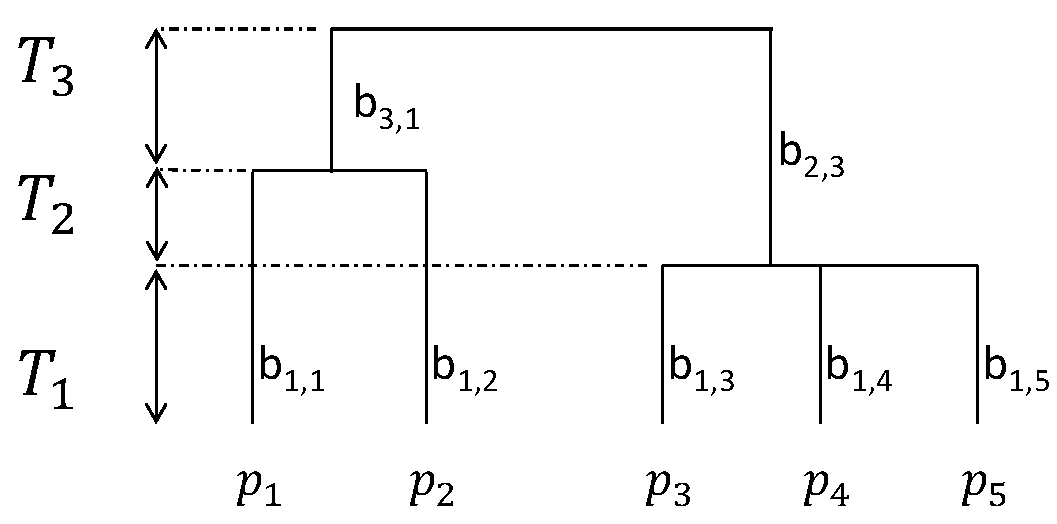
Figure 9.4: Arbre phylogénétique ou fonctionnel hypothétique. 5 espèces sont présentes (\(S=5\)), leurs probabilités notées \(p_1\) à \(p_5\). Les noms des branches sont affichés.

La diversité phylogénétique \(^{q}\!\bar{D}(T)\) appliquée à un arbre ultramétrique est un cas particulier de \(^q\!D^{\mathbf{Z}}\) pour une matrice \(\mathbf{Z}\) dont les lignes et colonnes sont la similarité des “espèces historiques” (Leinster et Cobbold 2012, proposition A7), c’est-à-dire les couples (espèce actuelle ; branche ancestrale).

Table 9.1: Table 9.2: Matrice de similarité correspondant à l’arbre phylogénétique en exemple. Les noms des lignes et colonnes sont les couples (espèce actuelle ; branche ancestrale).

	\((1;b_{1,1})\)	\((1;b_{3,1})\)	\((2;b_{1,2})\)	\((2;b_{3,1})\)	\((3;b_{1,3})\)	\((3;b_{2,3})\)	\((4;b_{1,4})\)	\((4;b_{2,3})\)	\((5;b_{1,5})\)	\((5;b_{2,3})\)
\((1;b_{1,1})\)	1	1	0	0	0	0	0	0	0	0
\((1;b_{3,1})\)	1	1	1	1	0	0	0	0	0	0
\((2;b_{1,2})\)	0	0	1	1	0	0	0	0	0	0
\((2;b_{3,1})\)	1	1	1	1	0	0	0	0	0	0
\((3;b_{1,3})\)	0	0	0	0	1	1	0	0	0	0
\((3;b_{2,3})\)	0	0	0	0	1	1	1	1	1	1
\((4;b_{1,4})\)	0	0	0	0	0	0	1	1	0	0
\((4;b_{2,3})\)	0	0	0	0	1	1	1	1	1	1
\((5;b_{1,5})\)	0	0	0	0	0	0	0	0	1	1
\((5;b_{2,3})\)	0	0	0	0	1	1	1	1	1	1

Par exemple, l’espèce 1 et les branches \(b_{1,1}\) et \(b_{3,1}\) fournissent les deux premières lignes et colonnes de la matrice ; l’espèce 5 et les branches \(b_{1,5}\) et \(b_{2,3}\), les deux dernières.

La diversité phylogénétique \(^{q}\!\hat{D}(T)\) est obtenue quand les éléments de la matrice \(\mathbf{Z}\) suivent les règles suivantes : les éléments de toutes les colonnes correspondant à une espèce donnée (par exemple les deux premières colonnes qui correspondent à l’espèce 1) valent 1 pour toutes les lignes correspondant à une branche dont l’espèce descend (les trois lignes correspondant aux branches \(b_{1,1}\) et \(b_{3,1}\)) ; les éléments dont l’espèce en colonne ne descend pas de la branche en ligne valent 0. La matrice n’est donc pas symétrique, mais c’est une matrice de similarité dont la diagonale vaut 1.

La probabilité de chaque espèce historique est la somme de celles des espèces actuelles qui en descendent, multipliée par la longueur de la branche normalisée par la hauteur de l’arbre. Dans l’exemple, la hauteur totale de l’arbre est \(T=T_1 + T_2 + T_3\). Les probabilités des espèces historiques sont \[(p_1 \frac{l(b_{1,1})}{T}, (p_1 + p_2) \frac{l(b_{3,1})}{T}, p_2 \frac{l(b_{1,2})}{T}, \dots, (p_3 + p_4 + p_5) \frac{l(b_{2,3})}{T}).\]

Les dimensions de la matrice de similarité et du vecteur de probabilités deviennent rapidement très grandes et leur écriture pénible : il est bien plus simple de calculer la diversité phylogénétique à partir des distances dans l’arbre et des probabilités des espèces. Cette équivalence de méthodes n’a donc pas d’intérêt pratique mais montre que la diversité de Leinster et Cobbold généralise la diversité phylogénétique. Cependant, le calcul de \(^q\!{\hat{D}}^{\mathbf{Z}}\) à partir d’une matrice \(\mathbf{Z}\) qui serait la simple transformation des distances de l’arbre phylogénétique, c’est-à-dire 1 moins les distances normalisées par la hauteur de l’arbre, ne donne pas la valeur de la diversité phylogénétique \(^{q}\!\bar{D}(T)\), sauf dans le cas particulier de la diversité de Rao, \(q=2\).

Pour un arbre non ultramétrique, il est possible de définir une matrice \(\mathbf{Z}\) similaire à celle de la table 9.1, mais ses valeurs non nulles ne sont pas égales à 1. Elles sont égales au rapport de \(\bar{T}\), la longueur moyenne des branches pondérée par la fréquence des espèces, sur la longueur de la branche : elles dépendent donc des fréquences des espèces et empêchent par conséquent la comparaison de la diversité entre communautés différentes.

9.8 Diversité individuelle

La diversité \(^q\!D^{\mathbf{Z}}\) et tous ses cas particuliers (phylodiversité et diversité neutre) peuvent être envisagés au niveau individuel plutôt qu’au niveau de l’espèce.

Le calcul de la diversité n’est pas affecté par le remplacement d’une espèce par deux espèces identiques. La ligne et la colonne de la matrice \(\mathbf{Z}\), correspondant à l’espèce \(s\) sont remplacées par deux lignes et colonnes identiques correspondant aux espèces \(s'\) et \(s''\), dont la similarité avec les autres espèces est la même que celle de l’espèce \(s\) et la similarité entre elles égale à 1, les probabilités vérifiant \(p_s=p_{s'}+p_{s''}\). L’opération peut être répétée jusqu’à la désagrégation complète de la matrice où chaque ligne correspondrait à un individu et les probabilités seraient égales à \({1}/{N}\). Il n’y donc pas de différence entre la mesure de la diversité individuelle et celle de la diversité spécifique qui n’est qu’une façon pratique de regrouper des individus ayant la même banalité. Dit autrement, l’entropie d’une communauté est la somme des entropie de ses espèces, qui n’est que la somme pondérée des entropies individuelles si tous les individus d’une espèce ont la même entropie.

La variabilité intraspécifique peut être traitée par un raisonnement similaire. L’idée d’intégrer aux mesures de diversité la possibilité que tous les individus d’une espèce ne soient pas semblables émerge dans la littérature (Pavoine et Ricotta 2014; Chiu et Chao 2014). Mais si des individus de la même espèce ne sont pas totalement similaires, ils ne peuvent pas être regroupés en prenant pour similarité de l’espèce avec elle-même une valeur unique qui résumerait la similarité entre les individus (au lieu de 1) pour tous les ordres de diversité.

Formellement, si l’espèce \(s\) est composée de deux groupes \(s'\) et \(s''\), la banalité du groupe \(s'\) est \[{\left(\mathbf{Zp}\right)}_{s'}=\sum_{t \ne s', s''}{p_{t}z_{s',t}} + p_{s'} + p_{s''}z_{s',s''},\] celle du groupe \(s''\) est \[{\left(\mathbf{Zp}\right)}_{s''}=\sum_{t \ne s', s''}{p_{t}z_{s'',t}} + p_{s'}z_{s',s''} + p_{s''}.\] Les similarités avec les autres espèces sont identiques : \(z_{s,t}=z_{s',t}=z_{s'',t}\). La contribution à la diversité des deux groupes \[\sum_{s'}{p_{s'}{\left(\mathbf{Zp}\right)}^{q-1}_{s'}}+\sum_{s''}{p_{s''}{\left(\mathbf{Zp}\right)}^{q-1}_{s''}}\] est remplacée après regroupement par \[\sum_{s}{p_{s}{\left(\mathbf{Zp}\right)}^{q-1}_{s}}.\] Puisque \(p_s=p_{s'}+p_{s''}\), le regroupement n’est possible quel que soit \(q\) que si les banalités des deux groupes sont identiques, ce qui interdit toute variabilité intraspécifique : \(z_{s',s''}\) est obligatoirement égal à 1. La non-linéarité de la moyenne généralisée ne permet pas de définir une matrice de similarité intégrant la variabilité intraspécifique.

Dans le cas de la diversité de Rao (\(q=2\)), on peut chercher la valeur de \(z_{s,s}\), différente de 1, définissant la similarité de l’espèce avec elle même pour prendre en compte sa variabilité. La résolution de l’équation \[\sum_{s'}{p_{s'}{\left(\mathbf{Zp}\right)}_{s'}}+\sum_{s''}{p_{s''}{\left(\mathbf{Zp}\right)}_{s''}} = \sum_{s}{p_{s}{\left(\mathbf{Zp}\right)}_{s}}\] permet de trouver \[z_{s,s}=1+ \frac{2 p_{s'} p_{s''}(z_{s',s''}-1)}{p_s^2}.\] Dans le cas le plus simple où \(p_{s'}=p_{s''}\), la similarité intraspécifique est \({(1+z_{s',s''})}/{2}\). La valeur de \(z_{s,s}\) peut être cherchée pour n’importe quelle valeur de \(q\), mais la résolution de l’équation est en général impossible analytiquement, et \(z_{s,s}\) varie avec \(q\). Se limiter à \(q=2\) simplifie le problème.

L’exemple suivant considère deux espèces, dont une comprenant deux groupes :

# Similarité entre les deux groupes
zs12 <- 0.9
# Probabilités des deux groupes
ps1 <- 1/5
ps2 <- 1/5
# Matrice de similarité
(Z2s <- matrix(c(1, zs12, 0.5, zs12, 1, 0.5, 0.5, 0.5, 1), nrow = 3))

##      [,1] [,2] [,3]
## [1,]  1.0  0.9  0.5
## [2,]  0.9  1.0  0.5
## [3,]  0.5  0.5  1.0

# Probabilités
(P2s <- c(ps1, ps2, 1 - ps1 - ps2))

## [1] 0.2 0.2 0.6

# Diversité
Dqz(P2s, 2, Z2s)

##     None 
## 1.329787

# Similarité intraspécifique après regroupement
(zss <- 1 + 2 * ps1 * ps2/(ps1 + ps2)^2 * (zs12 - 1))

## [1] 0.95

# Matrice de similarité après regroupement
(Z1s <- matrix(c(zss, 0.5, 0.5, 1), nrow = 2))

##      [,1] [,2]
## [1,] 0.95  0.5
## [2,] 0.50  1.0

# Probabilité après regroupement
(P1s <- c(ps1 + ps2, 1 - ps1 - ps2))

## [1] 0.4 0.6

# Diversité
Dqz(P1s, 2, Z1s)

##     None 
## 1.329787

En pratique, si les similarités entre individus ou groupes sont connues, le regroupement n’a aucun intérêt. Mais en absence de données individuelles, il est possible de choisir arbitrairement une similarité intraspécifique différente de 1 (ou de façon équivalente une distance différente de 0) pour calculer une diversité d’ordre fixé, de préférence 2.

9.9 Diversité des valeurs propres

L’approche de Pavoine et Izsák (2014) permet de prendre en compte la variabilité intraspécifique de façon rigoureuse. Pour mesurer la diversité neutre, les espèces sont placées dans un espace multidimensionnel, de dimension \(S\). Chaque espèce est représentée par un vecteur de longueur \(p_s\) sur son axe. Cette représentation a été utilisée par Campos et Isaza (2009) qui ont relié la diversité de Simpson au volume de la sphère sur laquelle se trouve le point définissant la communauté (figure 9.5).

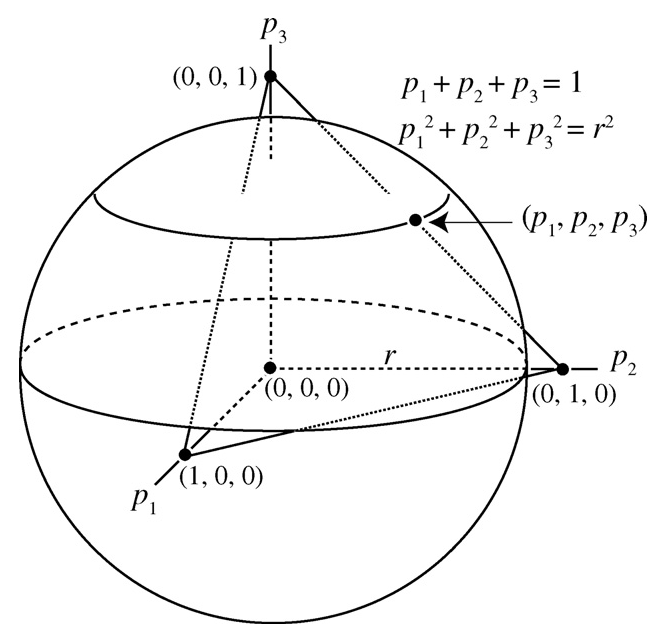
Figure 9.5: Représentation d’une communauté dans un espace multidimensionnel dont chaque axe correspond à une espèce. La communauté est composée de trois espèces. Le point représentant la communauté se trouve sur la sphère de rayon \(r=\sqrt{\sum_s{p_s^2}}\). Le plan (qui est en réalité un hyperplan de dimension \(S-1\)) d’équation \(\sum_s{p_s}=1\) est représenté par un triangle.

La matrice de similarité entre les espèces \(\mathbf{Z}\) permet d’affiner la représentation. Soit la matrice \(\mathbf{C}=\sqrt{\mathbf{Z}}\). Chaque espèce \(s\) est maintenant représentée par le vecteur dont la coordonnée sur l’axe \(t\) est \(\sqrt{p_s p_t}c_{s,t}\). Les axes correspondent aux espèces “pures”, totalement dissimilaires, les vecteurs des espèces réelles prennent en compte la similarité. Dans le cas extrême de la diversité neutre, \(\mathbf{C}=\mathbf{I}\), chaque espèce est située uniquement sur son axe. Dans l’autre cas extrême de totale similarité, où \(\mathbf{C}\) ne contient que des 1, toutes les espèces sont colinéaires.

Il est possible de calculer les \(S\) valeurs propres notées \(\lambda_s\) de la matrice des coordonnées des espèces et de les normaliser : \(\mu_s={\lambda_s}/{\sum_s{\lambda_s}}\). La communauté peut maintenant être représentée par ses valeurs propres \(\mu_s\) correspondant à la proportion d’une “espèce composite” pure sur chaque axe généré par les vecteurs propres : cette transformation est une ACP non centrée, non réduite. La diversité HCDT des valeurs propres est la diversité de la communauté, qui sera notée ici \(^q\!D^{\mathbf{Z}}(\Lambda)\).

La définition de cette diversité autorise toute matrice \(\mathbf{C}\) symétrique, dont les valeurs de similarité sont positives ou nulles, strictement positives sur la diagonale. Si \(\mathbf{C}\) est la racine carrée d’une matrice de similarité au sens strict \(\mathbf{Z}\), c’est-à-dire contenant des valeurs comprises entre 0 et 1 et dont les éléments de la diagonale sont tous égaux à 1, alors \(^2\!D^{\mathbf{Z}}(\Lambda)\) est égale à la diversité de Rao appliquée à une matrice de distances \(\mathbf{D}=1-\mathbf{Z}\). La définition de \(\mathbf{C}\) comme racine carrée de \(\mathbf{Z}\) se justifie par des raisons géométriques : la norme de chaque vecteur représentant une espèce est la racine carrée de la somme des carrés de ses coordonnées. Le carré de la norme du vecteur de l’espèce \(s\) est donc \(p_s\) multiplié par la banalité de l’espèce.

Si \(\mathbf{Z}=\mathbf{I}_s\), l’ACP ne modifie pas le nuage de points original et \(^q\!D^{\mathbf{Z}}(\Lambda)={^{q}\!D}\).

L’exemple suivant calcule la diversité de la méta-communauté Paracou618 selon la matrice de distances Paracou618.dist.

# Probabilités
Ps <- Paracou618.MC$Ps[Paracou618.MC$Ps > 0]
# Matrice de distances fonctionnelles
DistanceMatrix <- as.matrix(Paracou618.dist)
# Mise en correspondance de la matrice et du vecteur de
# probabilités
D <- DistanceMatrix[names(Ps), names(Ps)]
# Normalisation
D <- D/max(D)
# Transformation en matrice de similarité
Z <- 1 - D
# Matrice diagonale contenant les probabilités
Q <- diag(Ps)
# Matrice des espèces (les lignes de Sp sont les
# coordonnées des vecteurs)
Sp <- sqrt(Q) %*% sqrt(Z) %*% sqrt(Q)
# Valeurs propres normalisées
Lambda <- svd(Sp)$d
Mu <- Lambda/sum(Lambda)
# Comparaison des valeurs à q=2
Diversity(Mu, 2)

##     None 
## 1.540061

# Diversité de Rao
Dqz(Ps, 2, Z)

##     None 
## 1.490786

# La valeur à q=0 est le nombre d'espèces
Diversity(Mu, 0)

## None 
##  229

length(Ps)

## [1] 229

La valeur de la diversité des valeurs propres est différente de celle de la diversité de Rao à cause des approximations numériques liées au calcul des valeurs propres (qui nécessitent l’inversion d’une matrice carrée de dimension \(S\)). La valeur exacte est celle donnée par Dqz().

Le profil de diversité se trouve en figure 9.6.

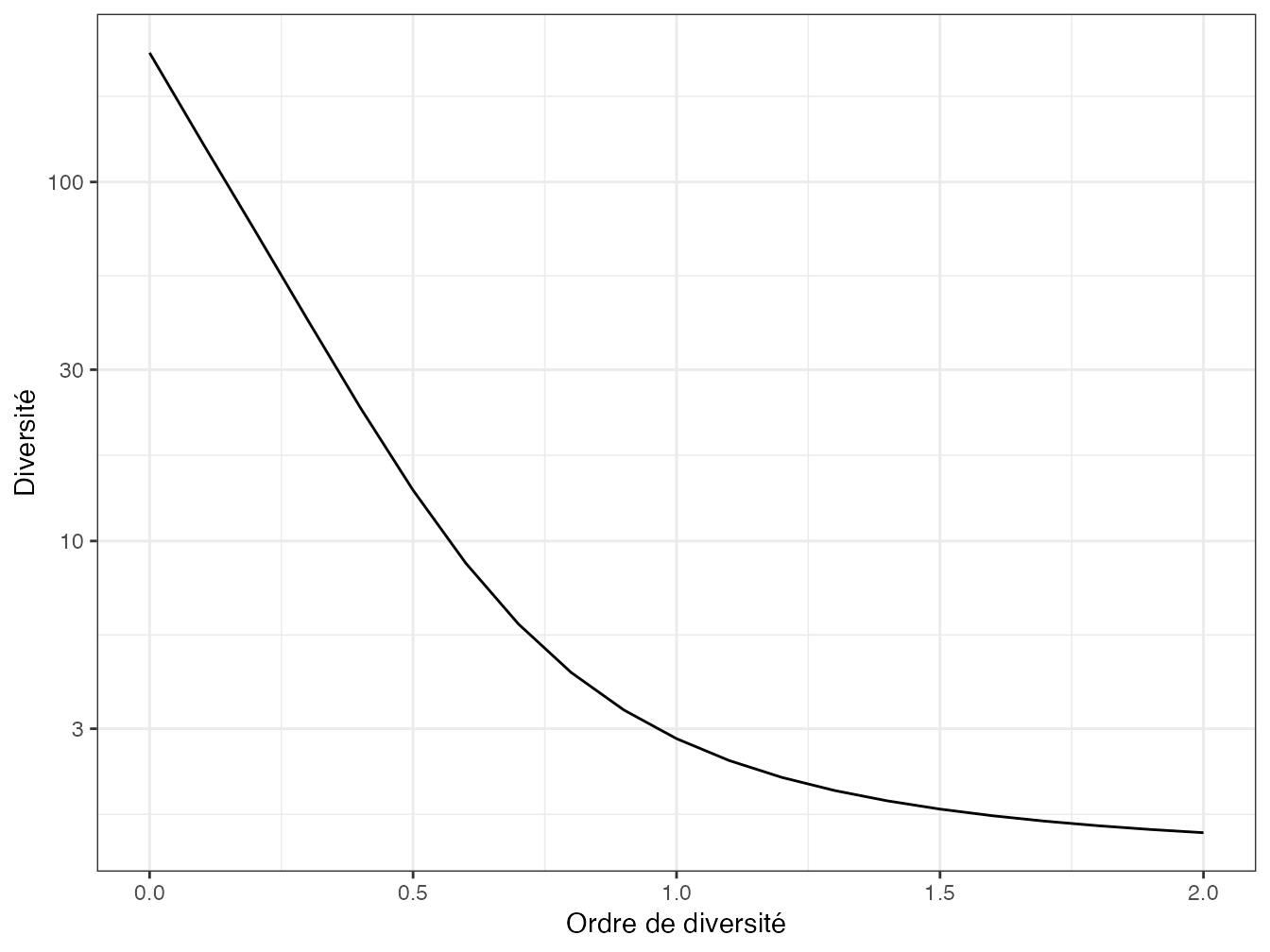
Figure 9.6: Profil de diversité des valeurs propres de la méta-communauté Paracou618.

Code R pour la figure :

DqZLambda <- CommunityProfile(Diversity, Mu)
Xlab <- "Ordre de diversité"
Ylab <- "Diversité"
autoplot(DqZLambda, xlab = Xlab, ylab = Ylab) + scale_y_log10()

La diversité des valeurs propres permet de ramener le problème de la diversité d’espèces partiellement similaires au calcul de la diversité neutre d’une communauté d’espèces composites totalement dissimilaires.

Les éléments de la diagonale de la matrice de similarité ne sont pas forcément égaux à 1 : des valeurs inférieures correspondent à la variabilité intraspécifique, selon le mécanisme de regroupement traité au paragraphe précédent. Les raisons qui empêchent d’utiliser des valeurs de similarité intraspécifique différentes de 1 dans le calcul de la diversité de Leinster et Cobbold ne s’appliquent pas ici : quelle que soit la valeur de \(q\), les valeurs propres sont les mêmes.

Les limites de la diversité des valeurs propres sont cependant nombreuses. La première est numérique : son calcul est imprécis dans des communautés très riches. L’inversion d’une matrice de dimension 200 ou plus est toujours problématique.

Les espèces non échantillonnées entraînent un biais d’estimation : le nombre de dimensions est sous-estimé. Comme les espèces manquantes ont une faible probabilité, leur vecteur est petit et n’influe pas beaucoup sur la diagonalisation de la matrice. Les valeurs propres manquantes sont donc petites. Elles influent sur la diversité pour les faibles valeurs de \(q\), notamment la diversité d’ordre 0 qui est le nombre de dimensions de la matrice des espèces (en général, le nombre d’espèces, ou une valeur inférieure si des espèces sont colinéaires). Il n’existe pas de technique pour corriger ce biais d’estimation.

La composition de la communauté en espèces composites dépend à la fois de la matrice de similarité et des probabilités des espèces réelles. Elle est donc unique pour chaque communauté, ce qui empêche toute décomposition de la diversité selon les méthodes présentées plus loin.

9.10 Synthèse

\(^{q}\!D(T)\) est l’exponentielle d’ordre \(q\) de la moyenne pondérée de l’entropie HCDT calculée à chaque période de l’arbre phylogénétique.

\(^q\!D^{\mathbf{Z}}\) est l’exponentielle d’ordre \(q\) de l’entropie de Ricotta et Szeidl, mais aussi l’inverse de la banalité moyenne des espèces de la communauté.

\(^q\!D^{\mathbf{Z}}\) et \(^{q}\!D\) sont des nombres effectifs d’espèces, respectent toutes les propriétés demandées à une mesure de diversité dont le principe de réplication. Leurs valeurs sont identiques pour \(q=2\) (diversité de Rao). \(^q\!D^{\mathbf{Z}}\) est moins sensible au paramètre \(q\) que \(^{q}\!D(T)\) : la figure 9.7 compare les deux mesures.

Le rôle du paramètre est assez différent : dans \(^q\!D^{\mathbf{Z}}\), la banalité des espèces est à la puissance \(q\) alors que leur probabilité est à la puissance 1. Le paramètre détermine l’importance donnée aux espèces originales, c’est-à-dire dont la banalité est petite, et non aux espèces rares. Les deux notions se confondent quand la diversité neutre est considérée : la banalité d’une espèce se réduit alors à sa fréquence.

Figure 9.7: Diversité phylogénétique (l’arbre est une taxonomie) d’ordre \(q\) de deux hectares de forêt de Paracou : \(^q\!D^{\mathbf{Z}}\) (trait plein) et \(^{q}\!\hat{D}(T)\) (pointillé).

Le code R nécessaire pour réaliser la figure est :

q <- c(seq(0, 3, 0.1))
# Réutilisation de Paracou618.Taxonomy au format phylog
# (cf. calcul de FAD)
DistanceMatrix <- as.matrix(Tree$Wdist^2/2)
Z <- 1 - DistanceMatrix/max(DistanceMatrix)
Divqz <- sapply(q, function(q) Dqz(Paracou618.MC$Ps, q, Z))
Divq <- sapply(q, function(q) ChaoPD(Paracou618.MC$Ps, q = q,
    PhyloTree = Paracou618.Taxonomy))
ggplot(data.frame(q, Divq, Divqz), aes(q)) + geom_line(aes(y = Divqz)) +
    geom_line(aes(y = Divq), lty = 2) + labs(y = "Diversité")

\(^q\!D^{\mathbf{Z}}\) est particulièrement intéressante pour mesurer la diversité fonctionnelle, souvent définie à partir d’une matrice de distances entre les espèces. La transformation d’une matrice en un arbre phylogénétique déforme les données (Pavoine, Ollier, et Dufour 2005; Podani et Schmera 2006, 2007). La diversité de Leinster et Cobbold est calculée directement à partir de la matrice.

Si l’arbre phylogénétique n’est pas ultramétrique, le calcul de la diversité est possible, mais la matrice \(\mathbf{Z}\) contient alors des valeurs comprises entre 0 et 1 qui dépendent des effectifs des espèces actuelles (ils interviennent dans le calcul de la hauteur de l’arbre qui est la moyenne de la longueur des branches). La dépendance entre similarité et fréquence des espèces constitue un problème théorique qui empêche d’interpréter la diversité calculée à partir d’un arbre non ultramétrique.

Enfin, il est possible de désagréger les données jusqu’au niveau individuel si la distance entre paires d’individus est connue. En revanche, la prise en compte de la variabilité intraspécifique par une similarité intraspécifique inférieure à 1 n’est possible que pour un ordre de diversité fixé : il n’est pas possible d’obtenir un profil de diversité de cette façon.