20 Indice $\alpha$ de Fisher

L’Indice $\alpha$ de Fisher est la pente de la relation linéaire entre le nombre d’espèces observées et le logarithme du nombre d’individus inventoriés. Cette relation correspond à une distribution d’abondance des espèces en log-séries, valide à l’échelle de la méta-communauté. Son utilisation à l’échelle locale est discutable.

Le modèle de Fisher (Fisher, Corbet, et Williams 1943) aboutissant à la SAD en log-séries, a marqué l’histoire de l’écologie. Il lie le nombre d’espèces au logarithme du nombre d’individus de façon linéaire dès que l’effectif est suffisant : la pente de la droite est le bien connu indice $\alpha$, tombé en désuétude pendant quelques décennies mais remis en vedette par la théorie neutre de Stephen P. Hubbell (2001). Il est utilisé à l’échelle locale (probablement à tort) et à l’échelle régionale, c’est pourquoi il est présenté en premier.

20.1 Construction

Le nombre d’espèces échantillonnées dépend de l’effort d’échantillonnage.

Fisher a relié le nombre d’espèces $S^{n}$ au nombre d’individus $n$ échantillonnés à partir du modèle suivant :

Le nombre d’individus $N$ de l’échantillon suit une loi de Poisson de paramètre $\lambda$ par hypothèse : la surface est fixée, égale à 1, et les individus sont distribués totalement aléatoirement (avec la même probabilité partout, et indépendamment les uns des autres) ;
Étant donné la taille de l’échantillon $N$ et la probabilité $p_s$ d’échantillonner l’espèce $s$, l’espérance du nombre d’individus échantillonnés dans l’espèce $s$ est $Np_s$ ;
Le nombre d’individus réellement observé fluctue aléatoirement. Il suit une loi de Poisson d’espérance $\lambda_s$, où $\lambda_s=\lambda p_s$ ;
La probabilité d’observer $\nu$ individus de l’espèce $s$ est notée ${\pi}_{s,\nu}$ ;
La distribution de $\lambda_s$ retenue par Fisher est une loi gamma de paramètres $k$ et $p$, choisie pour ses propriétés mathématiques qui impliquent que ${\pi}_{s,\nu}$ suit une loi binomiale négative de paramètres $k$ et $1/(p+1)$ ;
L’espérance du nombre d’espèces observées $\nu$ fois est $\sum_s{{\pi}_{s,\nu}}$ ;
Le paramètre $k=0$ décrit bien les données de Fisher et permet de calculer l’espérance du nombre d’espèces dans un échantillon de taille $n$.

Le raisonnement est détaillé ici. La loi gamma a deux paramètres positifs notés $k$ et $p$ par Fisher : le premier fixe sa forme, le second l’échelle. Les valeurs de forme inférieures à 1 donnent une distribution décroissante présentée sur la figure 20.1. La distribution obtenue est celle de $\lambda_s$, l’espérance du nombre d’individus de l’espèce $s$. Le paramètre de d’échelle permet d’ajuster les nombres d’individus à la taille de l’échantillon. Il est forcément très supérieur à 1. Plus le paramètre de forme $k$ est proche de 0, plus la décroissance des probabilités est rapide.

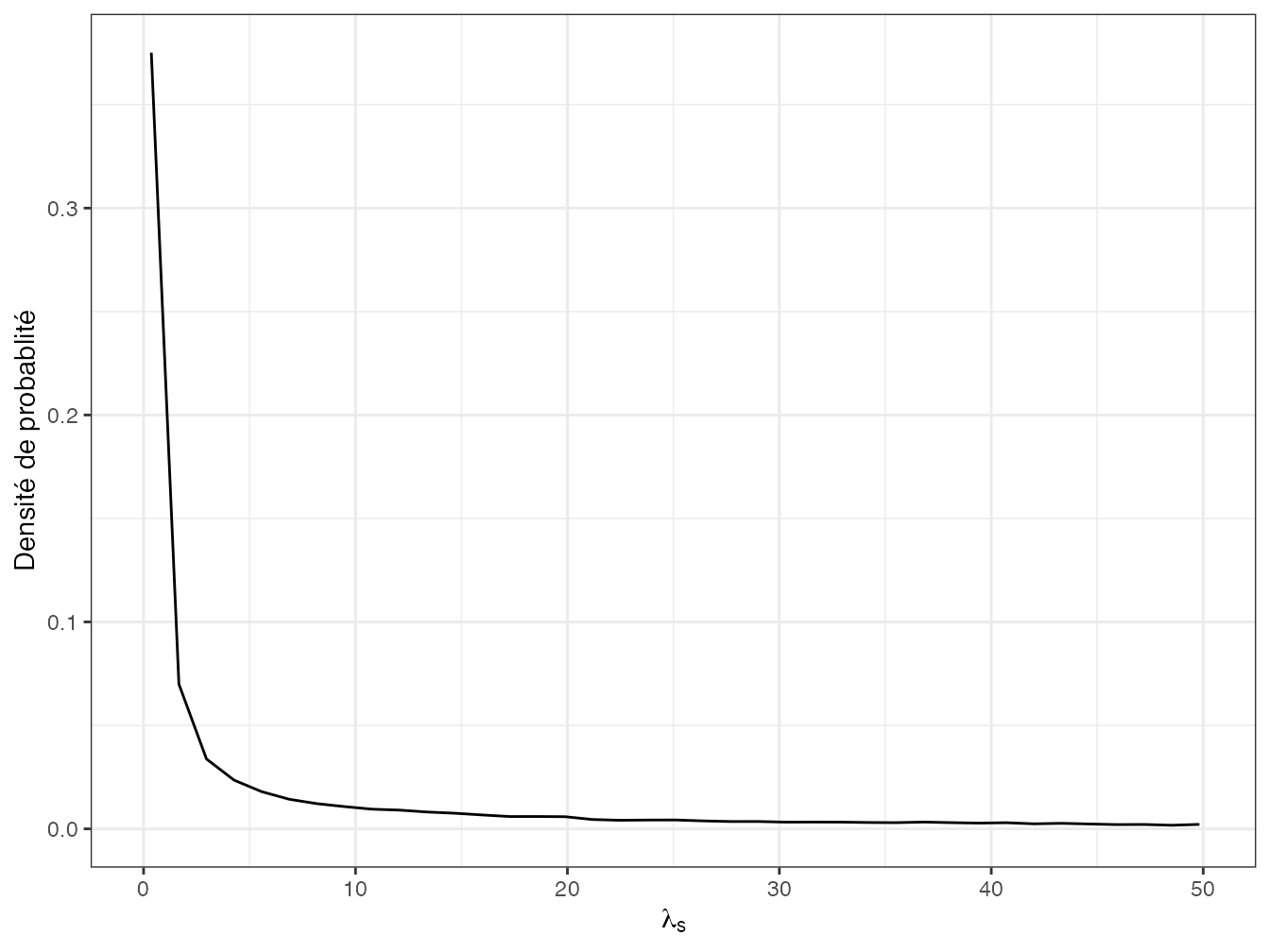
$Densité de probabilité d’une loi gamma de paramètres $0,2$ et 100. Seules les valeurs inférieures à 50 sont affichées.$

Figure 20.1: Densité de probabilité d’une loi gamma de paramètres $0,2$ et 100. Seules les valeurs inférieures à 50 sont affichées.

Le code R nécessaire pour réaliser la figure est :

library("GoFKernel")
k <- 0.2
p <- 100
d <- density.reflected(rgamma(10000, shape = k, scale = p), lower = 0)
ggplot(data.frame(d$x, d$y), aes(d.x, d.y)) +
  geom_line() +
  xlim(0, 50) +
  labs(x = expression(lambda[s]), y = "Densité de probablité")

Les effectifs de la communauté sont un mélange de lois de Poisson de paramètres aléatoires suivant tous la même loi gamma. La distribution des probabilités qui en résulte est une loi binomiale négative (Greenwood et Yule 1920). La probabilité qu’une espèce soit représentée par $\nu$ individus, notée ${\pi}_{s,\nu}$, suit donc une loi binomiale négative de paramètres $k$ et ${1}/{p+1}$ représentée sur la figure 20.2.

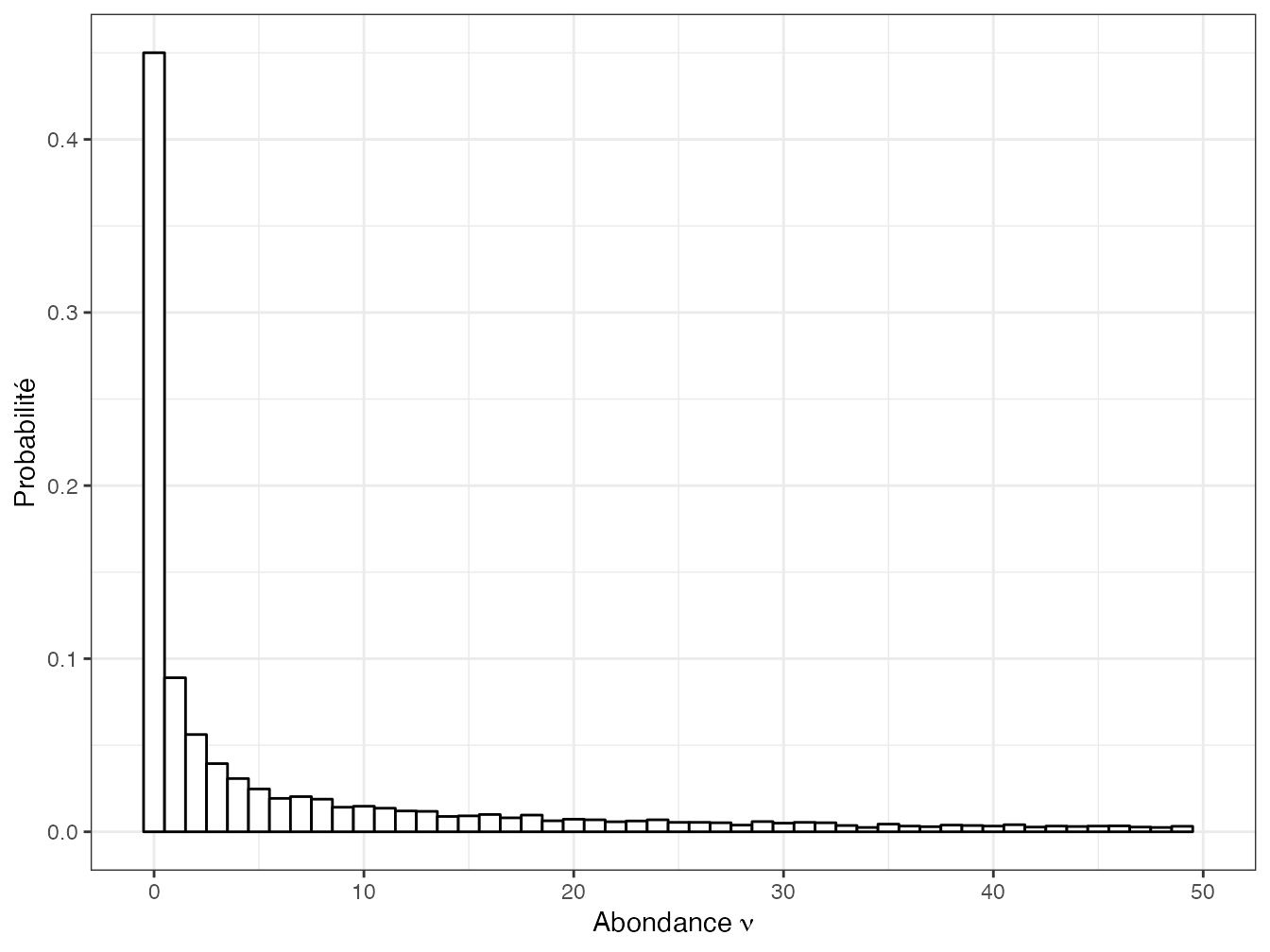
$Réalisation d’une loi gamma de paramètres $0,2$ et $100$. L’histogramme représente la proportion (qui estime la probabilité) des valeurs inférieures à 50. Les espèces d’abondance nulle ne sont pas observées dans l’échantillon.$

Figure 20.2: Réalisation d’une loi gamma de paramètres $0,2$ et $100$. L’histogramme représente la proportion (qui estime la probabilité) des valeurs inférieures à 50. Les espèces d’abondance nulle ne sont pas observées dans l’échantillon.

Le code R nécessaire pour réaliser la figure est :

nbin <- rnbinom(10000, size = k, prob = 1/(p+1))
ggplot(data.frame(nbin), aes(x = nbin, y = ..prop..)) + 
  geom_bar(width = 1, color = "black", fill = "white") +
  xlim(-0.5, 50) +
  labs(x = expression(paste("Abondance ", nu)), y = "Probabilité")

On notera que la distribution de ${\pi}_{s,\nu}$ décrit, pour une espèce, la probabilité d’être représentée par $\nu$ individus. Ce n’est pas la distribution des probabilités $p_s$, qui donnent la probabilité qu’un individu appartienne à l’espèce $s$. Une courbe représentant les valeurs de ${\pi}_{s,\nu}$ en fonction de leur rang n’est donc pas un diagramme rang-abondance, mais un “pseudo-RAC” (Izsák et Pavoine 2012).

La variance de la loi binomiale négative varie en sens inverse du paramètre $k$. En appliquant son modèle à des données, Fisher remarque que $k \to 0$, ce qui correspond à une distribution comprenant de nombreuses espèces de fréquences très variables, donc un pseudo-RAC décroissant rapidement, et retient cette propriété pour la suite de son raisonnement. La valeur nulle de $k$ simplifie les calculs et permet de calculer pour une valeur arbitraire de $\nu$ la somme sur toutes les espèces des valeurs de ${\pi}_{s,\nu}$. Dans ce cas, l’espérance du nombre d’espèces représentées par $\nu$ individus est, en posant $x=p/(p+1)$ et $\alpha$ une constante :

\[\begin{equation} \tag{20.1} {\mathbb E}\left(S^{n}_{\nu}\right) = \frac{\alpha}{\nu} x^\nu. \end{equation}\]

L’espérance du nombre d’espèces en est la somme pour toutes les valeurs de $\nu$ : \[\begin{equation} \tag{20.2} {\mathbb E}\left(S^{n}\right) = \sum_{\nu=1}^{\infty}{{\mathbb E}\left(S^{n}_{\nu}\right)} = -\alpha \ln(1-x). \end{equation}\]

Le nombre d’espèces est obtenu par la somme du développement en série entière du logarithme de $1-x$, d’où le nom de log-série.

De même, le nombre total d’individus est : \[\begin{equation} \tag{20.3} n = \sum_{\nu=1}^{\infty}{\nu {\mathbb E}\left(S^{n}_{\nu}\right)} = \sum_{\nu=1}^{\infty}{\alpha x^\nu} = \frac{\alpha x}{1-x}. \end{equation}\]

La combinaison des deux équations permet d’éliminer $x$ et d’obtenir l’espérance du nombre d’espèces observées en fonction de la taille de l’échantillon :

\[\begin{equation} \tag{20.4} {\mathbb E}\left( S^n \right) = \alpha\ln \left( 1 + \frac{n}{\alpha} \right). \end{equation}\]

$\alpha$ est un indicateur de la biodiversité qui peut être interprété comme le nombre d’espèces nouvelles découvertes quand le nombre d’individus échantillonnés est multiplié par $e$ : c’est en effet la pente de la courbe de $S^{n}$ en fonction de $\ln n$, qui se stabilise à partir d’une valeur de $n$ suffisante. C’est aussi le nombre de singletons attendus dans l’échantillon de taille $n$ comme le montre l’équation (20.1), sachant que $x \approx 1$.

$\alpha$ est aussi égal à $\theta$, le nombre fondamental de la biodiversité de Hubbell quand le nombre d’espèces est grand (Alonso et McKane 2004) : la SAD de la méta-communauté (pas celle de la communauté locale si la dispersion est limitée) du modèle neutre est en log-séries. $\alpha$ est le produit du nombre total d’individus de la méta-communauté, noté classiquement $J_m$, et du taux de spéciation individuel noté $\nu$. $x$ est le rapport entre les taux de naissance $b$ et de mortalité $d$ dans la méta-communauté, très légèrement inférieur à 1 parce que les espèces existantes sont appelées à disparaître par dérive, et remplacées par les nouvelles espèces : ${(b+\nu)}/{d}=1$.

Dans R, les fonctions fisher.alpha de la librairie vegan et fishers.alpha de la librairie untb (Hankin 2007) effectuent une résolution numérique de l’équation (20.4) pour estimer $\alpha$. La fonction optimal.theta dans untb évalue la valeur de $\theta$ par la méthode du maximum de vraisemblance (Stephen P. Hubbell 2001, 122), en utilisant toute l’information de la distribution. Le résultat est très différent parce que l’approximation de l’égalité de $\alpha$ et $\theta$ ne tient pas dans ce cas :

library("vegan")
data(BCI)
# Ns est un vecteur contenant les effectifs de chaque
# espèce
Ns <- colSums(BCI)
fisher.alpha(Ns)

## [1] 35.05477

library("untb")

## Registered S3 method overwritten by 'untb':
##   method       from 
##   plot.preston vegan

## 
## Attaching package: 'untb'

## The following objects are masked from 'package:dplyr':
## 
##     count, select

fishers.alpha(sum(Ns), length(Ns))

## [1] 35.05477

optimal.theta(Ns)

## [1] 80.95173

Le modèle de Fisher (20.4) peut être écrit sous la forme $\hat{S}^{n} = \alpha{\ln\left(\alpha+n\right)}-\alpha\ln\left(\alpha\right)$. Pour $n$ assez grand et sous l’hypothèse de saturation de Hubbell(Stephen P. Hubbell 2001), $A$ est proportionnel à $\alpha+n$ et le modèle de Fisher est équivalent au modèle de Gleason (Engen 1977).

Bordenave (Bordenave et De Granville 1998; Bordenave, De Granville, et Steyn 2011) propose un indice de richesse spécifique (IRS, ou SDI : Species Diversity Index) égal à la pente de la relation de Gleason. Dans le cadre de l’approximation précédente, il est égal à $\alpha$.

20.2 Variantes

Schulte, Lantinga, et Hawkins (2005) ont étendu le modèle de Fisher pour prendre en compte un nombre d’espèces fini $S$ et une distribution non indépendante des individus, prise en compte par un paramètre d’agrégation spatiale $c$ valable pour toutes les espèces :

\[\begin{equation} \tag{20.5} S^{n} = \frac{\alpha}{c} \ln\left(\frac{1+ n^c\,q}{1+ n^c\,q\,e^{-cS/\alpha}}\right), \end{equation}\]

où

\[\begin{equation} \tag{20.6} q =\frac{e^{c/\alpha}-1}{1-e^{c\left(1-S\right)/\alpha}}. \end{equation}\]

Si $S = \infty$ et $c = 1$, l’équation (20.5) se simplifie pour retrouver l’équation (20.4).

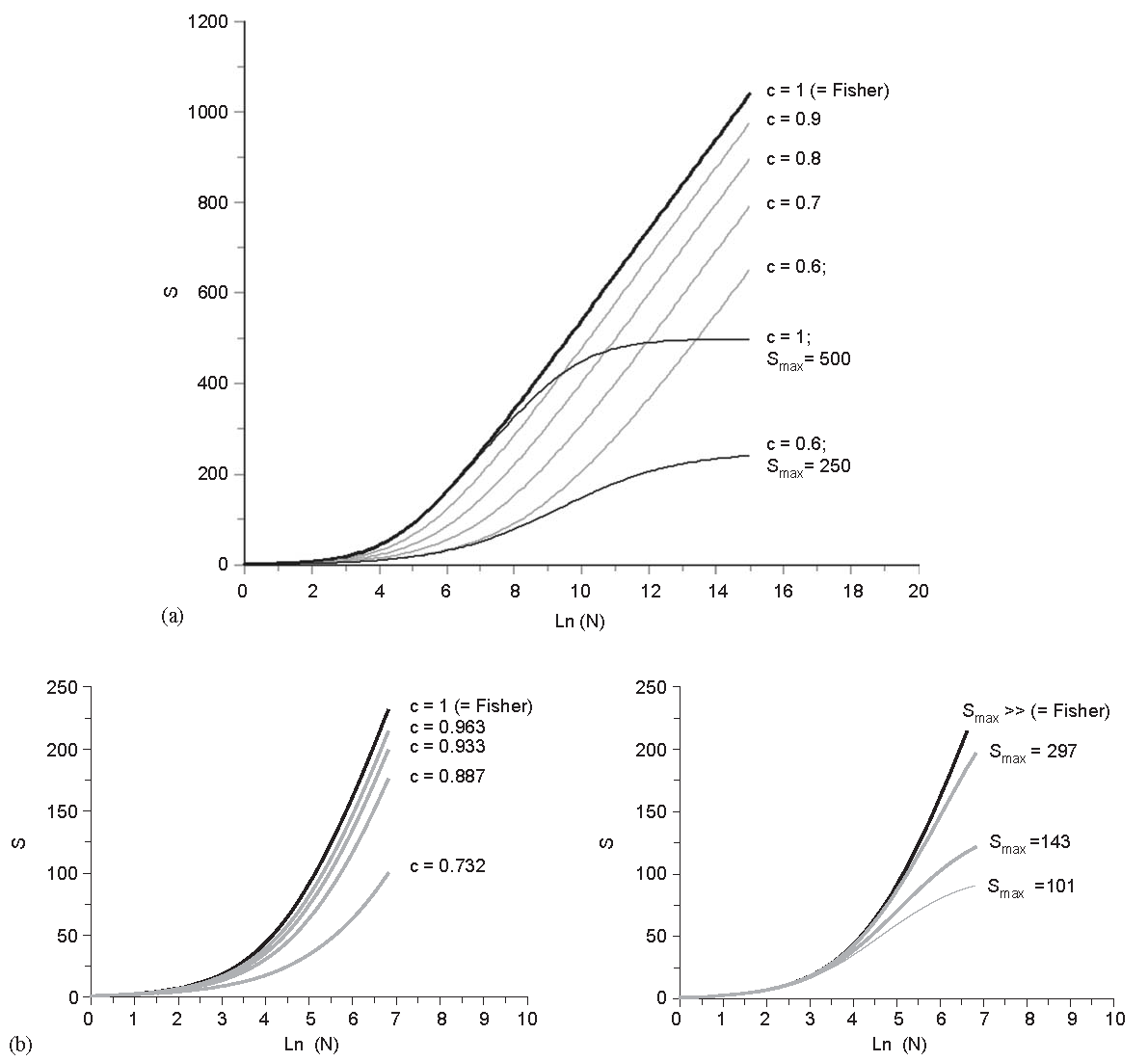
$Courbes nombre d’individus-espèces-simulées pour illustrer l’importance des paramètres $c$ (concentration spatiale) et $S_{\max}$ (nombre total d’espèces, $S$ dans nos notations) dans le modèle de Fisher. $\alpha$ est fixé à 100 pour toutes les courbes. (a) et (b) : la concentration spatiale ($c<1$) change drastiquement le nombre d’espèces attendu. En pratique, seuls $S$ et $N$ ($s^{n}_{\ne 0}$ et $n$ dans nos notations) sont observés. Si $c$ est supposé égal à 1 par erreur, $\alpha$ est sous-estimé. (a) et (c) : le nombre d’espèces n’est évidemment pas infini, ce qui change fortement la forme de la courbe. Si le nombre d’observations est grand, $\alpha$ sera aussi très sous-estimé.$

Figure 20.3: Courbes nombre d’individus-espèces-simulées pour illustrer l’importance des paramètres $c$ (concentration spatiale) et $S_{\max}$ (nombre total d’espèces, $S$ dans nos notations) dans le modèle de Fisher. $\alpha$ est fixé à 100 pour toutes les courbes. (a) et (b) : la concentration spatiale ($c<1$) change drastiquement le nombre d’espèces attendu. En pratique, seuls $S$ et $N$ ($s^{n}_{\ne 0}$ et $n$ dans nos notations) sont observés. Si $c$ est supposé égal à 1 par erreur, $\alpha$ est sous-estimé. (a) et (c) : le nombre d’espèces n’est évidemment pas infini, ce qui change fortement la forme de la courbe. Si le nombre d’observations est grand, $\alpha$ sera aussi très sous-estimé.

Leurs résultats (figure 20.3) montrent que la non prise en compte de ces deux paramètres aboutit à une sous-estimation systématique de $\alpha$, différente selon les sites, ce qui invalide les comparaisons inter-sites.

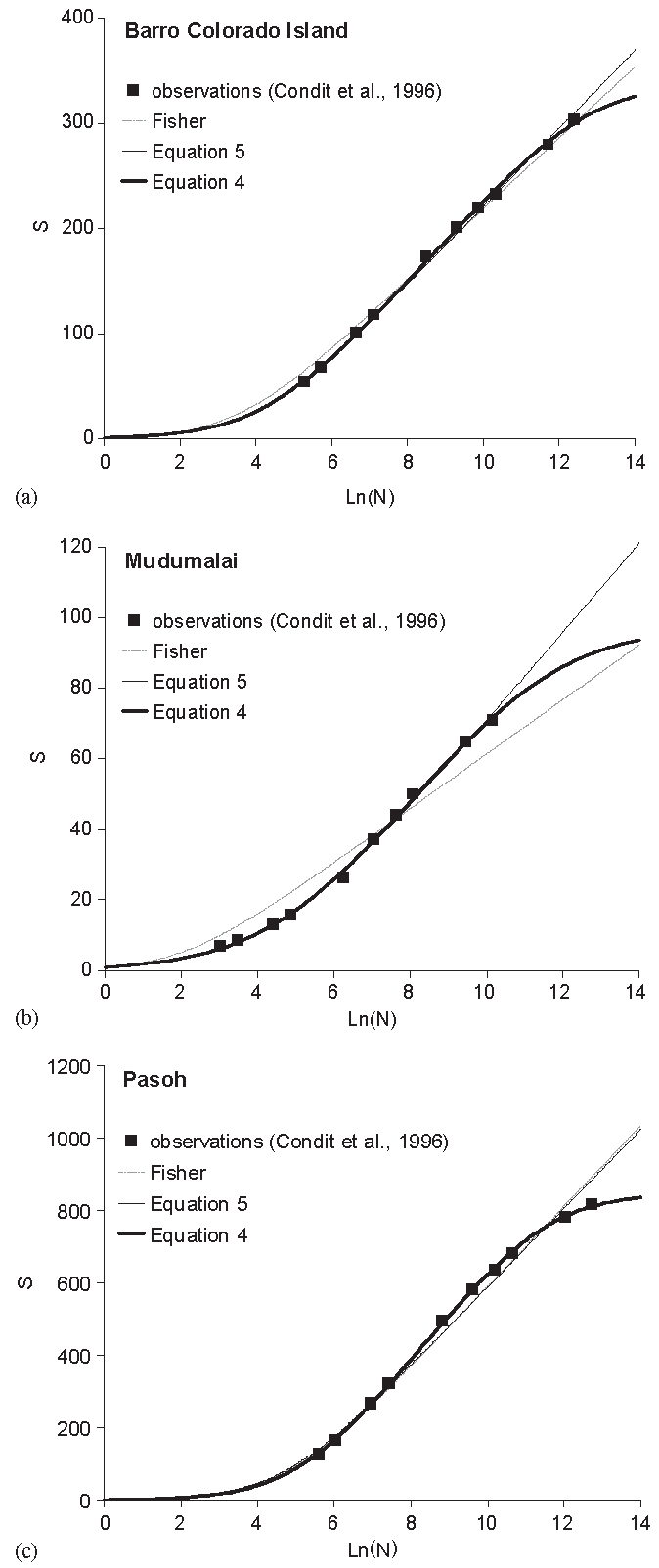
Comparaison entre le modèle de Fisher et le modèle étendu dans trois parcelles forestières connues. Les modèles sont ajustés aux données. Les courbes légendées Equation 4 correspondent au modèle de Fisher étendu par Schulte, alors que l’Equation 5 est le modèle intermédiaire, supposant le nombre total d’espèces infini.

Figure 20.4: Comparaison entre le modèle de Fisher et le modèle étendu dans trois parcelles forestières connues. Les modèles sont ajustés aux données. Les courbes légendées Equation 4 correspondent au modèle de Fisher étendu par Schulte, alors que l’Equation 5 est le modèle intermédiaire, supposant le nombre total d’espèces infini.

Appliqué à des données réelles (figure 20.4), le modèle de Fisher étendu s’ajuste forcément mieux (il possède trois paramètres au lieu d’un). L’approximation du nombre d’espèces infini paraît être la plus pénalisante parce qu’elle exclut l’inflexion de la courbe pour les grandes valeurs de $N$, même si ces valeurs sont rarement atteinte dans les faits ($e^{10}>20000)$.

L’indice de Fisher repose lourdement sur l’hypothèse que la distribution réelle des espèces est conforme au modèle. Jost (2007) montre par un exemple que des interprétations absurdes de l’indice peuvent être faites si l’hypothèse n’est pas respectée.

Kempton et Taylor (1976) et Kempton et Wedderburn (1978) ont défini l’indice $Q$ comme la pente de la courbe de $\hat{S}^{n}$ en fonction de $\log{n}$ mesurée entre le premier et le troisième quartile du nombre d’espèces observées, quelle que soit la distribution des espèces. $Q = \alpha$ si la distribution est en log-séries, et $Q = {c S}/{\sigma}$ si elle est log-normale ($c$ est une constante dépendant de la proportion des espèces échantillonnée, $S$ le nombre d’espèces total et $\sigma$ l’écart-type de la distribution du logarithme des probabilités).

La simulation suivante tire 10000 arbres dans le jeu de données BCI indépendamment et selon les fréquences des espèces. L’indice Q est calculé :

Ns <- colSums(BCI)
Inventaire <- rmultinom(10000, 1, Ns/sum(Ns))
# Cumul de l'inventaire
Cumul <- apply(Inventaire, 1, cumsum)
# Nombre d'espèces cumulées
nEspeces <- apply(Cumul, 1, function(x) length(x[x > 0]))
# Nombre total d'espèces
S <- max(nEspeces)
# Premier et troisièmes quartiles
Q13 <- which(nEspeces >= max(nEspeces)/4 & nEspeces <= max(nEspeces) *
    3/4)
nq1 <- min(Q13)
nq3 <- max(Q13)
Sq1 <- nEspeces[nq1]
Sq3 <- nEspeces[nq3]
# Indice Q
(Q <- (Sq3 - Sq1)/log(nq3/nq1))

## [1] 33.72253

La SAC correspondante est tracée en figure 20.5.

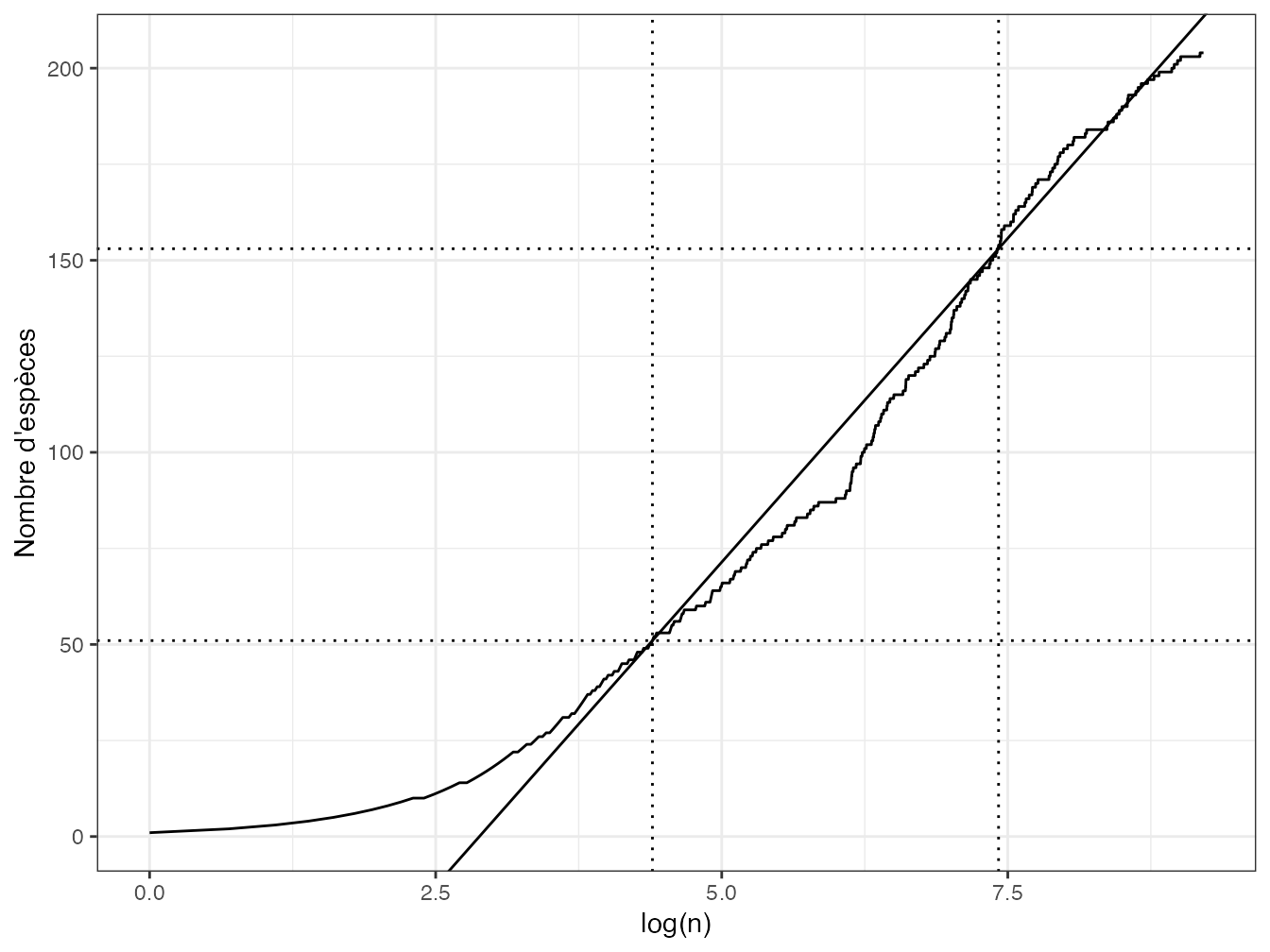
$SAC d’un inventaire simulé de 10000 arbres de BCI. Le nombre d’espèces cumulé est tracé en fonction du logarithme du nombre d’individus échantillonnés. $Q$ est la pente de la droite passant par les points de la courbe correspondant aux premier et troisième quartiles du nombre d’espèces.$

Figure 20.5: SAC d’un inventaire simulé de 10000 arbres de BCI. Le nombre d’espèces cumulé est tracé en fonction du logarithme du nombre d’individus échantillonnés. $Q$ est la pente de la droite passant par les points de la courbe correspondant aux premier et troisième quartiles du nombre d’espèces.

Code R pour réaliser la figure :

ggplot(data.frame(x = log(1:ncol(Inventaire)), y = nEspeces)) +
  geom_line(aes(x = x, y = y)) +
  geom_vline(xintercept = log(nq1), lty = 3) +
  geom_vline(xintercept = log(nq3), lty = 3) +
  geom_hline(yintercept = Sq1, lty = 3) +
  geom_hline(yintercept = Sq3, lty = 3) +
  geom_abline(intercept = Sq1-Q*log(nq1), slope = Q) +
  labs(x = "log(n)", y = "Nombre d'espèces")

19 Cadre

21 Accumulation de la diversité locale

Mesures de la Biodiversité

20 Indice \(\alpha\) de Fisher

20.1 Construction

20.2 Variantes