10 Cadre

La diversité \(\beta\) désigne la différentiation entre communautés, c’est-à-dire une mesure de divergence de composition spécifique entre elle, ou bien la divergence entre elles et leur assemblage, appelée diversité proportionnelle. La conciliation de ces deux définitions fait toujours l’objet de recherches.

La notion de diversité \(\beta\) a été introduite par Whittaker (1960), page 320, comme le niveau de changement dans la composition des communautés, ou le degré de différenciation des communautés, en relation avec les changements de milieu. La traduction de cette notion intuitive en une définition sans ambiguïté est encore une question de recherche et de débats.

Anderson et al. (2011) fournissent une revue des analyses utiles de la diversité \(\beta\) en forme de guide à destination des écologues reprise ici en introduction. La distinction entre diversité de différenciation et diversité proportionnelle est présentée ensuite.

Pour simplifier l’exposé, les individus seront échantillonnés dans des communautés, appartenant à une méta-communauté. Le tableau 10.1 résume les notations.

Des exemples montrent comment calculer cette diversité, principalement à l’aide du package entropart. Le package contient les données d’inventaire de deux hectares du dispositif de Paracou. Les données sont organisées dans le package sous la forme d’un objet MetaCommunity qui contient notamment la matrice des \(n_{s,i}\). Les parcelles de Paracou sont dans l’objet Paracou618.MC.

library(entropart)
summary(Paracou618.MC)

## Meta-community (class 'MetaCommunity') made of 1124 
## individuals in 2 communities and 425 species. 
## 
## Its sample coverage is 0.92266748426447 
## 
## Community weights are: 
## [1] 0.5720641 0.4279359
## Community sample numbers of individuals are: 
## P006 P018 
##  643  481 
## Community sample coverages are: 
##      P006      P018 
## 0.8943859 0.8463782

Table 10.1: Table 10.2: Notations des effectifs, tableau espèces-communautés.

	Communauté \(i\)	\(\dots\) Total : méta-communauté
Espèce \(s\)	\(n_{s,i}\) : nombre d’individus de l’espèce \(s\) dans la communauté \(i\). \(\hat{p}_{s|i}=n_{s,i}/n_{+i}\) est l’estimateur de la probabilité \(p_{s|i}\) qu’un individu de la communauté \(i\) soit de l’espèce \(s\).	\(n_{s+}=\sum_i{n_{s,i}}\). \(p_s=\sum_i{w_{i}p_{s|i}}\)
\(\dots\)
Total	\(n_{s+}=\sum_i{n_{s,i}}\). \(p_s=\sum_i{w_{i}p_{s|i}}\)	\(n\) : nombre total d’individus échantillonnés

10.1 Définition de la diversité \(\beta\) par objectifs

Anderson et al. (2011) proposent une revue des définitions de la diversité \(\beta\) selon les analyses écologiques auxquelles elles peuvent contribuer plutôt que selon leurs propriétés mathématiques.

Deux types de diversité \(\beta\) peuvent être définies (Vellend 2001) en accord avec les notions originales de Whittaker : le remplacement (turnover) des espèces le long d’un gradient environnemental, spatial ou temporel et la variation de la composition spécifique entre communautés, qui diffèrent de la méta-communauté et entre elles. Ces deux définitions sont présentées sur les figures 10.1 et 10.2 (Anderson et al. 2011).

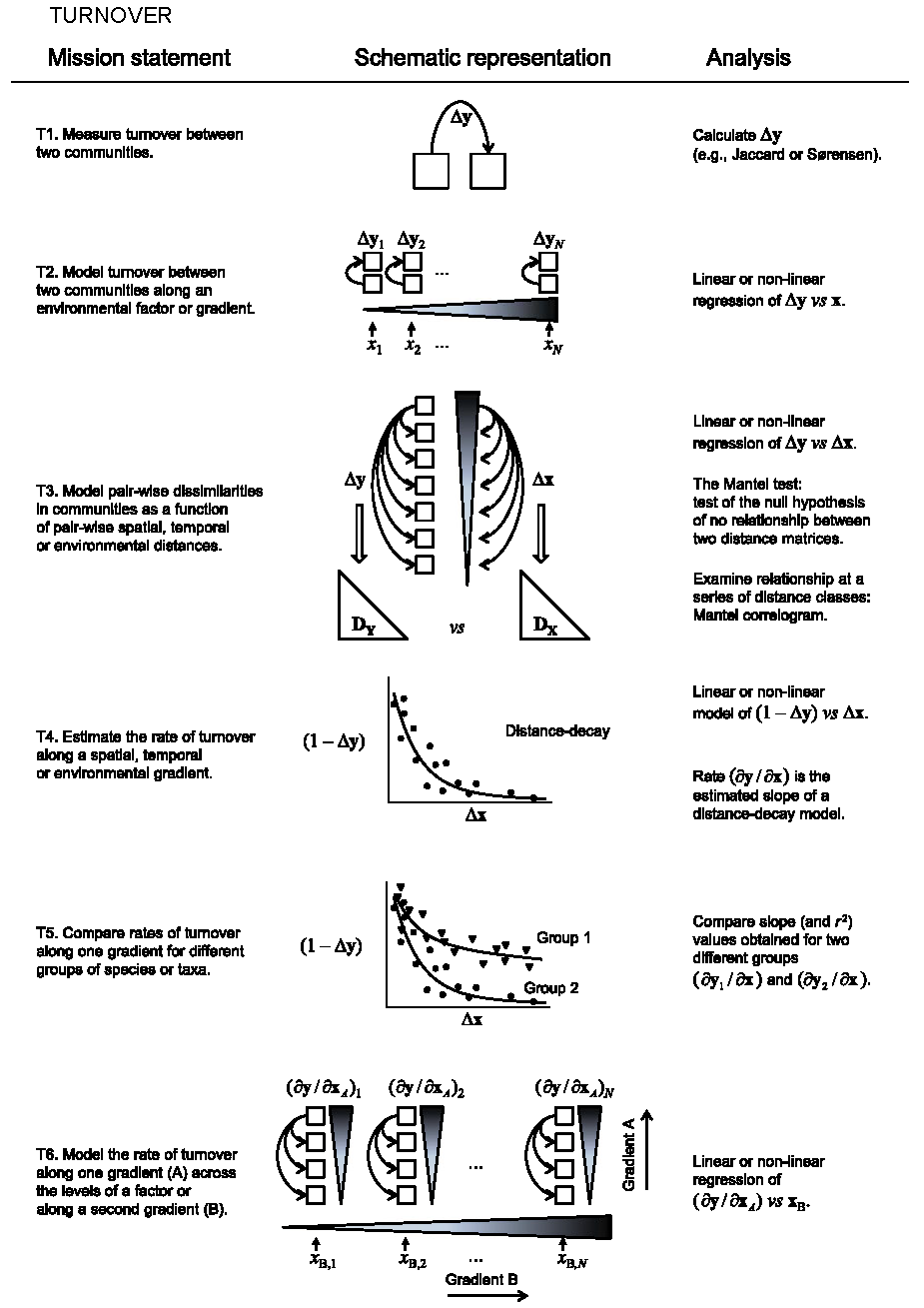
Figure 10.1: Diversité \(\beta\) liée au remplacement des espèces le long d’un gradient. \(\Delta{y}\) est la mesure de la dissimilarité entre deux communautés. \(\mathbf{x}\) est un gradient environnemental, spatial ou temporel. \(\Delta{x}\) est l’écart entre deux points du gradient.

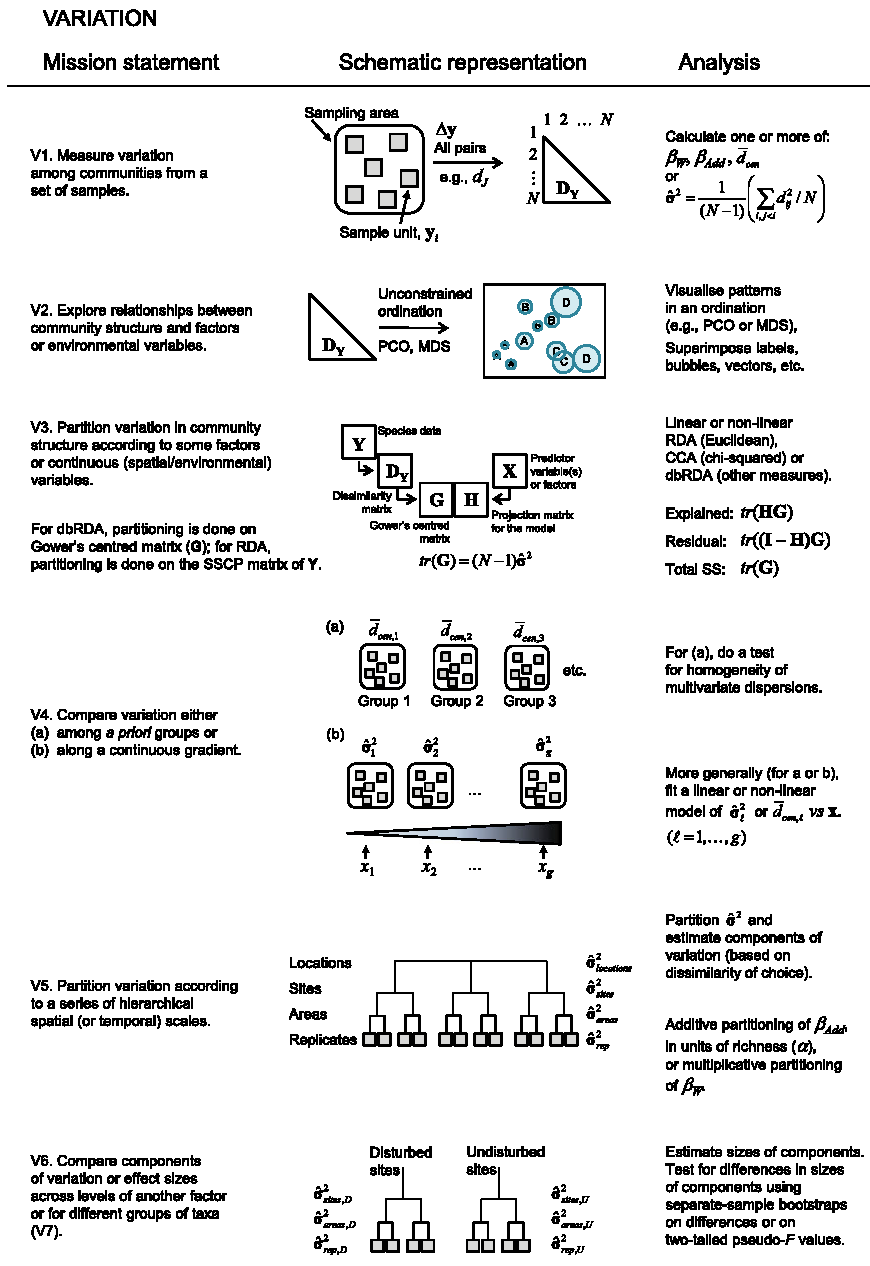
Figure 10.2: Diversité \(\beta\) liée à la variation de la composition spécifique. \(\beta_W\) est le rapport entre la diversité \(\gamma\) et la diversité \(\alpha\), \(\beta_{Add}\) leur différence. \(d_{ij}\) est la dissimilarité entre les communautés \(i\) et \(j\). \(\hat{\sigma}^2\) est la variance de cette dissimilarité, \(\bar{d}\) sa moyenne. Si \(d\) est une distance euclidienne, \(\bar{d}_{cen}\) est la distance moyenne des communautés à leur centre de gravité.

Les mesures de remplacement ne sont pas traitées en détail dans ce chapitre mais simplement présentées ici.

La plus simple (figure 10.1, T1) est la dissimilarité entre deux communautés notée \(\Delta{y}\). De nombreuses mesures de dissimilarité existent, elles sont détaillées dans le chapitre 11. Whittaker n’envisageait que la présence ou l’absence des espèces, mais leur abondance peut être prise en compte.

Cette dissimilarité peut être analysée en fonction du gradient de référence. La dissimilarité entre des paires de communautés présentant la même différence (par exemple ayant subi ou non un traitement) situées le long d’un gradient (par exemple la fertilité du sol) peut être analysée en fonction de ce gradient (figure 10.1, T2). Plus classiquement, la diversité \(\beta\) peut être régressée contre la valeur du gradient (T3). La dissimilarité de chaque paire de communautés est confrontée à son écart sur le gradient. Les deux analyses précédentes peuvent être combinées pour mesurer le remplacement des espèces selon deux gradients emboîtés (T6).

Une variation sur le modèle T2 consiste à le représenter sous la forme d’un modèle de décroissance en fonction de la distance (Nekola et White 1999), éventuellement pour plusieurs groupes de communautés (figure 10.1, T4 et T5). L’indice de Simpson spatialement explicite (Section 23.1) entre dans ce cadre bien qu’il soit construit différemment.

Les mesures de variation (figure 10.2, V1) concernent la dissimilarité entre plusieurs communautés ou entre chaque communauté et la méta-communauté. L’équivalence de ces deux concepts n’est pas évidente : elle a été montrée pour les mesures de dissimilarité entre paires de communautés par Legendre et Anderson (1999) ; Legendre et Gallagher (2001) ; Legendre, Borcard, et Peres-Neto (2005) et pour l’entropie de Rao par Pavoine, Dufour, et Chessel (2004) mais reste une question ouverte pour l’entropie HCDT en général.

La diversité \(\beta\) peut être mesurée pour un assemblage de communautés au choix comme la moyenne des dissimilarités entre les paires de communautés ou à partir des diversités \(\gamma\) et \(\alpha\), c’est-à-dire en tant que mesure dérivée. Cette dernière approche est traitée dans ce chapitre, où il sera montré que la mesure dérivée est aussi une dissimilarité moyenne entre communautés et méta-communauté.

Si la diversité est mesurée comme moyenne des dissimilarités, elle peut être analysée par des méthodes d’ordination indirectes (figure 10.2, V2) ou directes (V3). Elle peut aussi être comparée entre méta-communautés ou modélisée en fonction d’un gradient environnemental (V4), de façon similaire au modèle T6.

La diversité \(\beta\) peut être décomposée en niveaux hiérarchiques emboîtés (V5). Des tests statistiques sont nécessaires pour comparer les niveaux : par exemple, montrer que la diversité (inter) entre des communautés supposées différentes est significativement plus grande que celle (intra) des placettes d’échantillonnage de chacune d’entre elles, à la manière d’une analyse de variance (V6). D’autres analyses sont bien sûr envisageables, comme la comparaison de la forme de la courbe de dissimilarité moyenne entre paires de communautés en fonction de la distance à des patrons connus, issus de simulation de processus à identifier (Réjou-Méchain et al. 2011).

10.2 Typologie des mesures

Cette approche utilitaire est complétée par le cadre théorique de Jurasinski, Retzer, et Beierkuhnlein (2009) qui distinguent plusieurs types de mesures de diversité :

• La diversité d’inventaire (inventory diversity), qui traite des données récoltées sur une unité spatiale, ce qui correspond à la définition des diversités\(\ \alpha\) et \(\gamma\) ;
• La diversité de différenciation (differentiation diversity), qui mesure à quel point les unités spatiales sont différentes, ce qui correspond à la définition littérale de la diversité \(\beta\) de Whittaker ;
• La diversité proportionnelle (proportional diversity), diversité \(\beta\) qui se construit par différence ou rapport des diversités \(\gamma\) et \(\alpha\). Marcon et al. (2014) ont montré qu’avec une décomposition appropriée de la diversité, la diversité proportionnelle est aussi la divergence entre la distribution des communautés locales et celle de la méta-communauté : la diversité \(\beta\) mesure alors à quel point les unités spatiales sont différentes de leur assemblage plutôt qu’entre elles.

Dans son article fondateur, Whittaker (1960) définit la diversité \(\beta\) comme le niveau de changement dans la composition des communautés, la nomme “diversité secondaire” et lui attribue la lettre \(\beta\) en référence à la diversité “primaire” mesurable par l’indice \(\alpha\) de Fisher (Fisher, Corbet, et Williams 1943), voir le chapitre 20. Il illustre cette définition par une mesure de différentiation : l’indice de Jaccard, mais utilise ensuite une mesure proportionnelle : le rapport des indice \(\alpha\) de l’assemblage des communautés à sa moyenne sur les communautés. La conciliation des deux approches n’est pas simple. Gregorius (2016) montre notamment que les mesures habituelles de diversité proportionnelle ne rendent pas compte correctement de la différentiation.

10.3 Décomposition de la diversité

La façon de décomposer la diversité, aboutissant donc à une diversité \(\beta\) proportionnelle, ne fait pas consensus. Les éléments du débat sont présentés ici.

10.3.1 Définitions de la diversité \(\beta\), mesure dérivée

Tuomisto (2010a) passe en revue l’ensemble des définitions de la diversité \(\beta\) dérivée des diversités \(\gamma\) et \(\alpha\). Toutes ont en commun :

• Une définition de la mesure de diversité, appliquée à la diversité \(\gamma\), qui est généralement une des mesures vues dans le chapitre 3 ;
• Une définition de la diversité \(\alpha\), qui peut être par exemple :
  • La diversité locale mesurée dans chaque communauté, indépendamment de toute référence hors de la communauté ;
  • De façon équivalente, le nombre d’espèces effectives dans les communautés.
  • Une façon de combiner les diversités \(\gamma\) et \(\alpha\) pour obtenir la diversité \(\beta\), par exemple :
    • \(\beta={\gamma}/{\alpha}\) ;
    • \(\beta=\gamma-\alpha\).

L’utilisation des nombres de Hill, la mesure locale de la diversité \(\alpha\) et la définition de la diversité \(\beta\) comme rapport des diversités \(\gamma\) et \(\alpha\) permet de définir la “vraie diversité” (Jost 2006, 2007) \(\beta\) qui est un nombre de communautés équivalentes (compositionnal units) similaire au nombre d’espèces équivalentes des diversités \(\alpha\) et \(\gamma\). Tuomisto (2011) milite pour que le terme diversité soit réservé à la vraie diversité (homogène à un nombre d’espèces) et que les autres mesures soient appelées différemment : “entropie” de Shannon ou “probabilité” de Gini-Simpson notamment.

10.3.2 Le débat sur la décomposition

L’objectif est de décomposer la diversité totale, notée \(\gamma\) en une composante inter-groupes, notée \(\beta\) et une composante intra-groupes notée \(\alpha\).

Whittaker (1960, 1972) est l’auteur de ce concept. Il a posé le principe que la diversité \(\gamma\) devait être le produit des diversités \(\alpha\) et \(\beta\).

Lande (1996) a une approche additive et postule que les mesures de diversité doivent être concaves : la diversité d’un jeu de données regroupant plusieurs communautés doit être supérieure ou égale à la somme pondérée des diversités dans chaque communauté. De cette façon, il est possible de définir une diversité totale égale à la somme pondérée des diversités \(\alpha\) (intra-communautés) et \(\beta\) (inter-communautés), toutes les diversités étant positives ou nulles. Il note que “la partition serait plus facilement interprétable si les différentes composantes de la diversité pouvaient être exprimés au moyen de la même formule” (ce qui n’est en fait jamais le cas). Une revue sur les avantages de la décomposition additive est proposée par Veech et al. (2002).

Un débat assez stérile a découlé de l’opposition entre les deux approches, principalement dû à la transformation logarithmique (Ricotta 2009b), à des définitions imprécises et des démonstrations empiriques remises en question (Baselga 2010a; Veech et Crist 2010). Il reste que la décomposition multiplicative permet seule la définition de la diversité \(\beta\) en tant que diversité au sens strict (Chao, Chiu, et Hsieh 2012).

Marcon et al. (2012) montrent que l’entropie de Shannon \(H_{\beta}\) est une mesure de diversité de différenciation en donnant sa définition indépendamment de \(H_{\alpha}\) et \(H_{\gamma}\), comme l’avaient fait Ricotta et Marignani pour l’entropie quadratique de Rao (Ricotta et Marignani 2007). C’est également une diversité proportionnelle, comme toutes les mesures passées en revue par Tuomisto : la diversité de Shannon permet d’unifier les deux approches.

L’indice de Shannon, couplé à son expression sous forme de nombre de Hill, respecte finalement tous les critères imposés ou souhaités. Sa décomposition est détaillée ci-dessous. Enfin, Marcon et al. (2014) généralisent ce résultat à toutes les mesures de diversités dérivées de l’entropie généralisée de Tsallis.

10.3.3 Décomposition multiplicative de la diversité

Jost (2007) et Chao, Chiu, et Hsieh (2012) ont montré que la décomposition des nombres de Hill en éléments indépendants est multiplicative :

\[\begin{equation} \tag{10.1} ^{q}\!D_{\gamma} = ^{q}\!D_{\alpha} ^{q}\!D_{\beta}. \end{equation}\]

\(^{q}\!D_{\alpha}\) et \(^{q}\!D_{\gamma}\) sont les nombres de Hill d’ordre \(q\) égaux aux diversités \(\alpha\) et \(\gamma\). Ce sont des nombres équivalents d’espèces. \(^{q}\!D_{\beta}\) est le “nombre de communautés effectives” ou “nombre équivalent de communautés”, c’est-à-dire le nombre de communautés de poids égal ne possédant aucune espèce en commun (et dont la dissimilarité entre les espèces de communautés différentes est maximale quand la diversité est phylogénétique ou fonctionnelle) (Pavoine, Marcon, et Ricotta 2016), qui fourniraient la même valeur de diversité \(\beta\).

La diversité \(\beta\) est indépendante de la diversité \(\alpha\) si les poids des communautés sont égaux. L’indépendance signifie que la valeur de \(^{q}\!D_{\beta}\) n’est pas contrainte par celle de \(^{q}\!D_{\alpha}\). Cette propriété est souvent considérée comme importante (M. V. Wilson et Shmida 1984; Gregorius 2010), et sera discutée largement ici.

10.3.4 Définitions de la diversité \(\alpha\)

La diversité \(\alpha\) est calculée pour chaque communauté, et notée \(^q_iD_{\alpha}\) (l’entropie correspondante est notée \(^{q}_{i}\!H_{\alpha}\)). La diversité \(\alpha\) de la méta-communauté est intuitivement la moyenne de celle des communautés. En raison de leurs propriétés mathématiques, il est plus simple de considérer la moyenne des entropies \(\alpha\).

Le poids de chaque groupe est \(w_i\), souvent choisi égal au nombre d’individus de la communauté divisé par le nombre total ou à la surface de chaque groupe, mais qui peut être arbitraire, tant que \(p_s=\sum_i{w_i p_{s|i}}\). Deux façons de pondérer la somme émergent de la littérature (Chao, Chiu, et Hsieh 2012). La définition classique est selon Routledge (1979)

\[\begin{equation} \tag{10.2} ^{q}\!H_{\alpha} = \sum_i{w_i {^{q}_{i}\!H_{\alpha}}}; \end{equation}\]

\[\begin{equation} \tag{10.3} ^{q}\!D_{\alpha}={\left(\sum_s{\sum_i{w_i p^q_{s|i}}}\right)}^{1/{\left(1-q\right)}}. \end{equation}\]

La pondération proposée par Jost (2007) est

\[\begin{equation} \tag{10.4} ^{q}\!H_{\alpha} = \sum_i{\frac{w^q_i}{\sum_i{w^q_i}} {^{q}_{i}\!H_{\alpha}}}; \end{equation}\]

\[\begin{equation} \tag{10.5} ^{q}\!D_{\alpha} = {\left(\sum_s{\sum_i{\frac{w^q_i}{\sum_i{w^q_i}}p^q_{s|i}}}\right)}^{{1}/{\left(1-q\right)}}. \end{equation}\]

La première est la pondération naturelle. La seconde, qui utilise les poids à la puissance \(q\), donne donc d’autant moins d’importance que \(q\) est grand aux communautés dont le poids est faible. Les deux définitions se confondent pour \(q=1\).

Si les poids sont différents, Jost (2007) a montré que l’indépendance n’est possible que si la diversité \(\alpha\) est définie selon sa pondération. En revanche, cette pondération ne garantit pas que la diversité \(\gamma\) soit supérieure à la diversité \(\alpha\) si \(q\) n’est égal ni à 0 ni à 1. Jost conclut donc que la décomposition n’est possible que pour des communautés de même poids ou pour \(q=0\) ou \(q=1\). Ricotta (2009a) contourne cette difficulté en proposant une méthode de ré-échantillonnage qui permet d’égaliser les poids.

Chiu, Jost, et Chao (2014) établissent une nouvelle définition de la diversité \(\alpha\) qui permet d’assurer l’indépendance et garantit que la diversité \(\beta\) est positive quels que soient les poids des communautés :

\[\begin{equation} \tag{10.6} ^{q}\!D_{\alpha}=\frac{1}{I}{\left(\sum_s{\sum_i{{\left(w_ip_{s|i}\right)}^q}}\right)}^{{1}/{\left(1-q\right)}}. \end{equation}\]

Cette définition pose problème : alors que le choix de \(q\) a pour but de donner une importance plus ou moins grande aux espèces rares, son effet est le même sur la taille des communautés La diversité dépendra essentiellement des espèces rares dans les communautés de faible poids si \(q\) est petit, définissant une diversité bi-dimensionnelle. Cette question est traitée en détail au chapitre 18.

Marcon et al. (2014) préfèrent la définition de Routledge qui est plus intuitive et garantit que la diversité \(\gamma\) est supérieure à la diversité \(\alpha\). La dépendance entre \(^{q}\!D_{\beta}\) et \(^{q}\!D_{\alpha}\) est le prix à payer.