21 Accumulation de la diversité locale
La courbe d’accumulation (SAC) décrit comment la richesse, ou la diversité, augmente en fonction de l’effort d’échantillonnage. Sous l’hypothèse d’un tirage multinomial des individus observés, les formules de raréfaction (estimation du nombre d’espèces pour une surface inférieure à celle inventoriée) sont bien contenues. La structure spatiale rend les observations dépendantes entre elles et doit être prise en compte.
Les propriétés des courbes d’accumulation ont été largement étudiées dans la littérature, notamment pour prédire la richesse spécifique (section 3.1.3).
L’influence de la structure spatiale est considérable mais souvent négligée parce que difficile à prendre en compte. Quelques méthodes sont pourtant applicables.
21.1 Courbes d’accumulation
On suppose que la communauté locale est de taille fixe et contient donc un nombre fixe d’espèces, et que leur découverte progressive aboutira à une asymptote de la SAC.
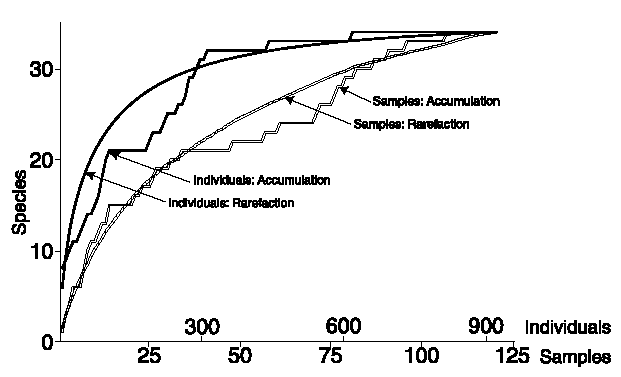
Figure 21.1: Courbes d’accumulation et de raréfaction, obtenues par inventaires individuels ou groupés (samples). Les courbes de raréfaction permettent de lisser les courbes d’accumulation. Les courbes obtenues par inventaire groupé sont en général en dessous des courbes individuelles à cause de l’agrégation spatiale.
Gotelli et Colwell (2001) proposent une revue des problèmes les plus communément rencontrés dans l’estimation et la comparaison de la richesse spécifique. Ils suggèrent notamment de calculer la courbe de raréfaction (figure 21.1) plutôt que d’utiliser la courbe d’accumulation obtenue en traçant simplement le nombre d’espèces découvert en fonction de l’effort d’échantillonnage. La courbe de raréfaction est obtenue en sous-échantillonnant dans l’inventaire complet des effectifs de toutes tailles et en calculant le nombre moyen d’espèces trouvé pour chacun, ce qui permet de la lisser. La formulation exacte de la courbe de raréfaction et de sa variance est connue (Ugland, Gray, et Ellingsen 2003).

Figure 21.2: Courbe d’accumulation des espèces d’arbres de Barro Colorado Island. Calcul par specaccum : accumulation des 50 carrés avec permutations.
La fonction specaccum de la librairie vegan (Oksanen et al. 2012) permet de tracer les SAC (figure 21.2) selon différentes méthodes, avec un intervalle de confiance obtenu par permutation de l’ordre d’ajout des données ou à partir des formules de raréfaction.
Le code R nécessaire pour réaliser la figure est :
data(BCI)
SAC <- specaccum(BCI, "random")
plot(SAC, ci.type = "poly", lwd = 2, ci.lty = 0, ci.col = "lightgray")Pour une surface donnée, le nombre d’individus est une variable aléatoire. Dans ce cas, la SAC (dépendant de la surface) est différente de la courbe de raréfaction (fonction du nombre d’individus) de Gotelli et Colwell, que Coleman (1981) nomme “courbe du collecteur”.
La SAC théorique en fonction de la surface contient une incertitude concernant le nombre d’individus. Si la densité \(\lambda_s\) (nombre d’individus par unité de surface) des espèces peut être connue (estimée en comptant les individus) ou si les probabilités \(p_s\) sont issues d’un modèle (log-séries, log-normal…), le nombre d’individus observés de l’espèce \(s\) suit une loi de Poisson d’espérance \(A\hat{\lambda}_s\) ou, de façon équivalente (Pielou 1969, 204‑5), \(np_s\) (dans ce deuxième cas, \(n\) est l’estimateur de \(N\), la variable aléatoire correspondant à la taille de l’échantillon).
La SAC théorique en fonction du nombre d’individus ne contient pas cet aléa. Le nombre d’individus de l’espèce \(s\) suit alors une loi binomiale d’espérance \(np_s\) et la distribution d’un échantillon de taille \(n\) suit la loi multinomiale correspondante. Les deux approches se réconcilient en fixant arbitrairement le nombre d’individus échantillonnés dans la courbe aire-espèce : conditionnellement au nombre total d’individus, la distribution des abondances des espèces issues de lois de Poisson de paramètres \(\lambda_s\) suit une loi multinomiale (Steel 1953) dont les probabilités sont proportionnelles à \(\lambda_s\).
La SAC définie en fonction du nombre d’individus est au sens strict une succession de points (à chaque valeur de \(n\)), pas une courbe continue. Elle est toutefois toujours présentée comme une courbe lissée passant par les points pour être continue et dérivable.
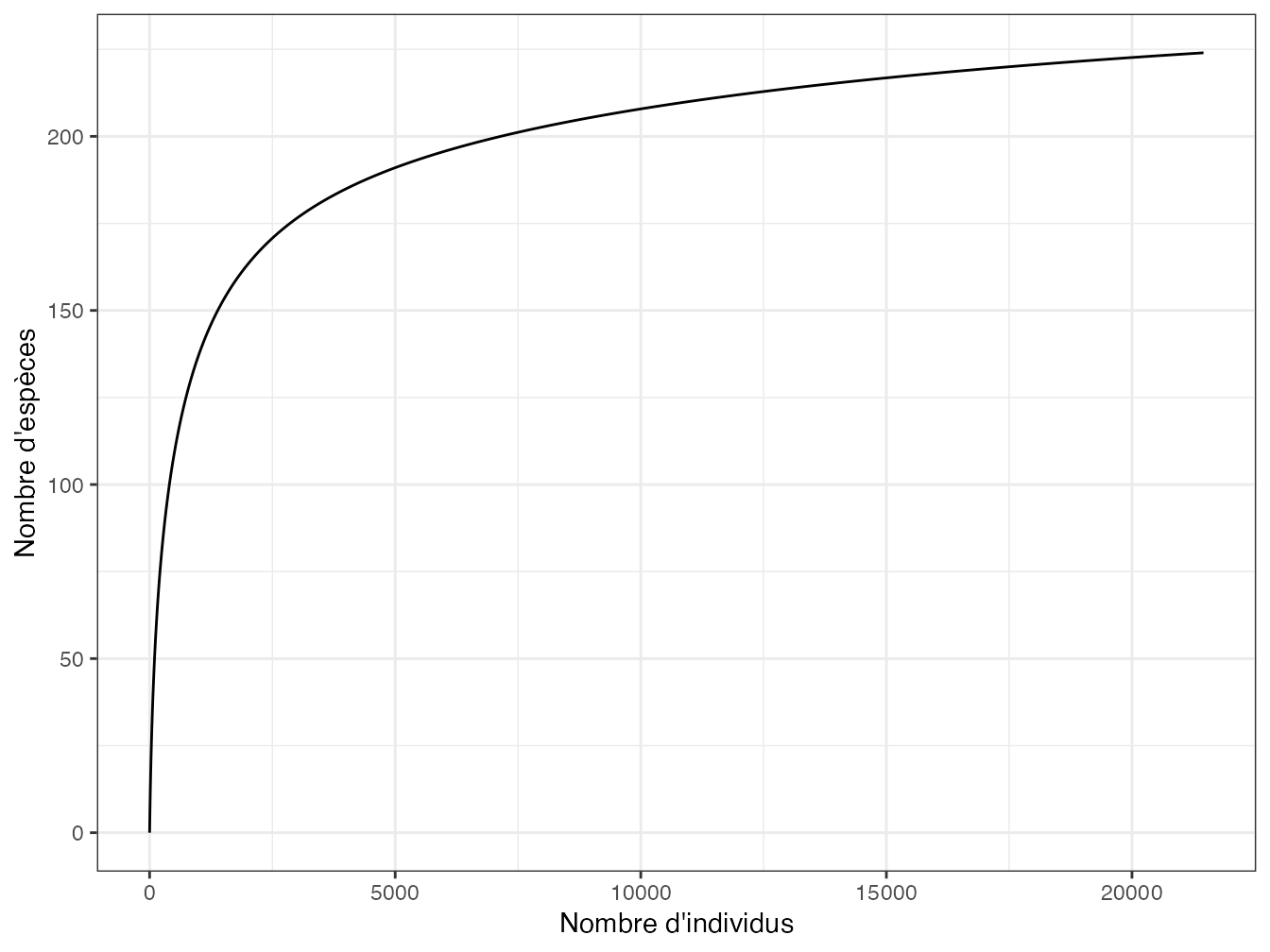
Figure 21.3: Courbe d’accumulation des espèces d’arbres de Barro Colorado Island. Somme des entropies de Simpson généralisées.
Une difficulté supplémentaire consiste à prendre en compte les espèces non échantillonnées en appliquant des techniques statistiques pour réduire le biais qu’elles induisent (Colwell et al. 2012). Dans ce but, la SAC théorique peut être construite (Chao, Wang, et Jost 2013) comme la somme des entropies de Simpson généralisées (Z. Zhang et Zhou 2010), présentées en section 4.7.3.
La courbe obtenue (figure 21.3) est la même que par raréfaction, sans les problèmes d’estimation.
Son intervalle de confiance n’est pas représenté : l’estimation est sans biais et a une variance très petite ; d’autre part, la variabilité de l’échantillonnage prise en compte dans la figure 21.2 est ignorée ici. La fonction GenSimp.z est fournie par le package EntropyEstimation (Cao et Grabchak 2014).
Code pour la figure :
21.2 Extrapolation
L’extrapolation de la SAC est un cas particulier de celle de la diversité, déjà vue en section 4.6.8.
Béguinot (2015b) a une approche différente. Il considère la SAC comme une fonction continue et infiniment dérivable de la taille de l’échantillon. Le nombre d’espèces non observées dans un échantillon de taille \(n\) est noté \(s^{n}_{0}\). Le nombre d’espèces observées dans la SAC est \(s^{n}_{>0} = S - s^{n}_{0}\). Quand \(n\) est assez grand, la pente de la SAC varie peu entre \(n-1\) et \(n+1\) individus. Béguinot (2014) approxime la dérivée de \(s^{n}_{0}\) par \(s^{n}_{0}-s^{n-1}_{0}\). La dérivée est en réalité plus grande : la pente de la SAC, qui est l’opposée de la pente de \(s^{n}_{0}\), décroît avec \(n\) mais l’approximation est acceptable quand \(n\) est assez grand. De même, les dérivées successives, par exemple seconde, sont approchées par la variation de la dérivée d’ordre inférieur, par exemple première, entre \(n-1\) et \(n\). En combinant ces approximations avec l’espérance du nombre d’espèces observées \(\nu\) fois dans un échantillon de taille \(n\), équation (3.2), on obtient : \[\begin{equation} \tag{21.1} {\mathbb E}\left( s^{n}_{\nu} \right) = \left(-1 \right)^{\nu-1} \binom{n}{\nu} \frac{\partial^\nu s^{n}_{>0}}{\partial n^\nu}, \nu=1,2,\dots \end{equation}\]
L’espérance du nombre d’espèces observées \(\nu\) fois dépend directement de la dérivée \(\nu\) de la SAC.
Béguinot (2015b) écrit l’accroissement du nombre d’espèces observées quand l’échantillon augmente de \(n\) à \(n +\delta n\) sous la forme d’une série entière, qu’il combine avec l’équation précédente pour en obtenir une approximation : \[\begin{equation} s^{n +\delta n} \approx s^{n} + \sum_\nu {\left(-1 \right)^{\nu-1} s^{n}_{\nu} \left(\frac{\delta n}{n}\right)^{\nu}}. \end{equation}\]
La somme est infinie mais ses termes décroissent rapidement. Le nombre de termes à prendre en compte est d’autant plus grand que \(\frac{\delta n}{n}\), le niveau d’extrapolation, est grand. L’auteur conseille de ne pas pousser l’extrapolation au delà du double de \(n\).
Cette méthode est comparée à l’extrapolation de la diversité d’ordre 0 (section 4.6.8) et à l’estimateur de T.-J. Shen, Chao, et Lin (2003) (section 3.1.1.8) dans l’illustration suivante.
Une communauté théorique log-normale de 300 espèces est créée. Des inventaires de 1000 individus sont simulés et les trois méthodes d’extrapolation de la richesse spécifique sont appliquées pour estimer la richesse d’un échantillon de 1800 individus. Les résultats obtenus sont comparés à des inventaires directs de 1800 individus.
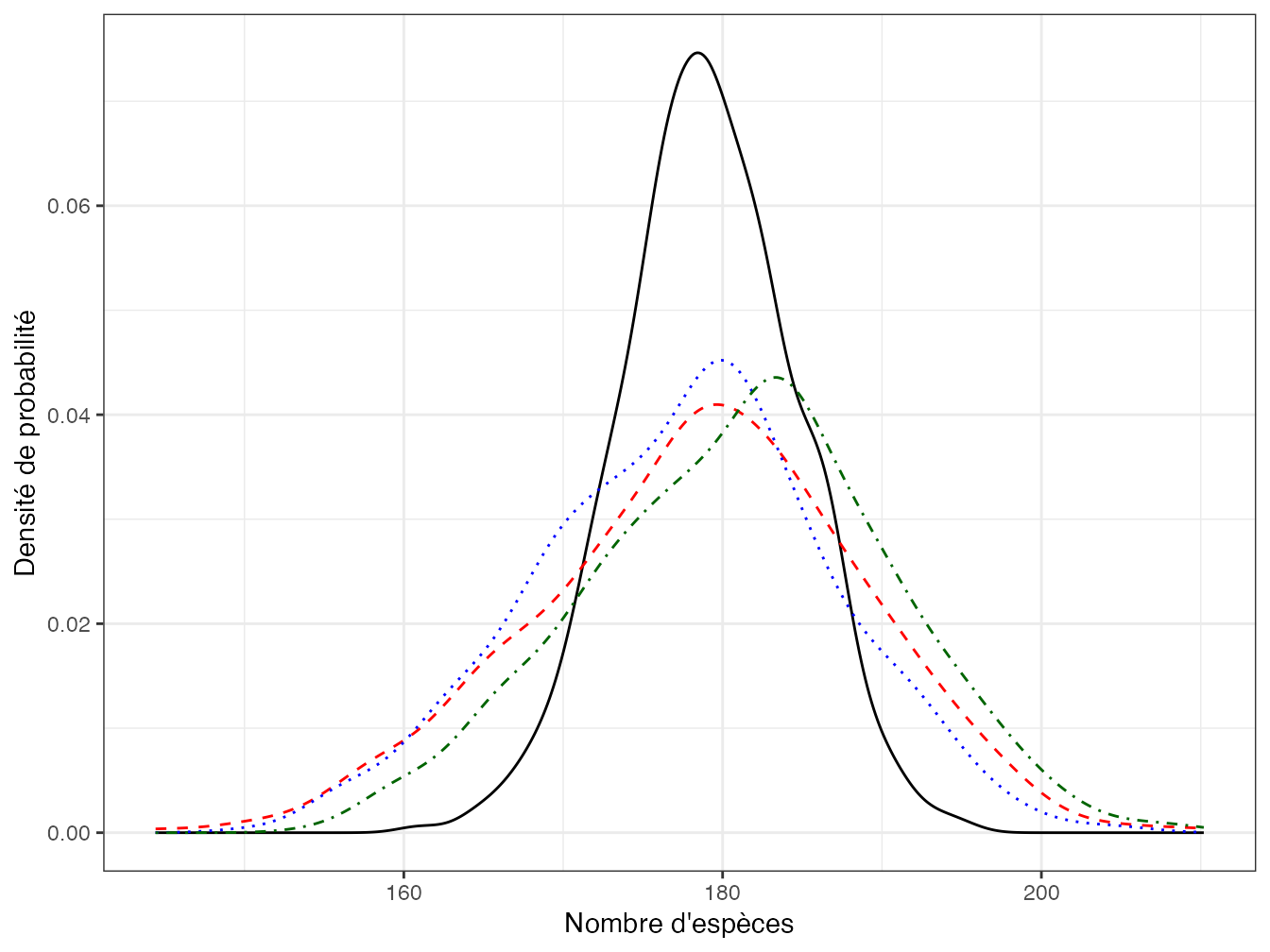
Figure 21.4: Distribution de la richesse obtenue par extrapolation à 1800 individus de 500 inventaires de 1000 individus selon les méthodes de Shen et al. (pointillés alternés vert), Béguinot (tirets rouges) ou Chao, Gotelli et al. (pointillés bleu). La distribution de la richesse de 500 inventaires de même taille est représentée par la courbe noire.
La figure 21.4 montre que les extrapolations sont bonnes et très similaires avec les trois méthodes. La distribution des 500 simulations d’extrapolation est proche de celle des 500 inventaires, avec une plus grande variabilité due à la quantité plus faible de données disponibles.
Le code R nécessaire pour réaliser la figure est :
# Ecart-type de la communauté log-normale
sdlog <- 2
# Nombre d'espèces
S <- 300
# Tirage des probabilités log-normales (l'espérance est sans importance)
Ps <- as.ProbaVector(rlnorm(S, 0, sdlog))
# Taille de l'inventaire
n <- 1000
# Niveau d'extrapolation
extra <- 0.8
# Nombre de simulations
nSim <- 500
# Création de nSim inventaires de n individus
Samples <- rmultinom(nSim, n, Ps)
# Richesse observée
S0 <- colSums(Samples > 0)
# Fonction d'extrapolation selon Béguinot
ExtrapolateB <- function(Ns) {
# Création d'un tableau contenant le nombre d'espèces par abondance
f <- AbdFreqCount(Ns)
# Calcul des termes de la somme
s <- sapply(1:nrow(f), function(i)
(-1)^(f[i, 1]-1) * f[i,2] * extra^f[i, 1])
return(sum(s))
}
# Extrapolation des inventaires
eB <- apply(Samples, 2, ExtrapolateB) + S0
# Extrapolation selon Chao, Gotelli et al. (2014)
ei <- apply(Samples, 2, Richness, Level = n*(1 + extra),
RCorrection = "Chao1")
# Fonction d'extrapolation selon Shen et al.
library("SPECIES")
ExtrapolateS <- function(Ns) {
# Nombre d'espèces non observées
sink(tempfile()) # Suppression des messages de jackknife()
S0 <- jackknife(AbdFreqCount(Ns))$Nhat -sum(Ns > 0)
sink() # restauration de l'affichage normal
# Taux de couverture
C <- Coverage(Ns)
# Espèces nouvelles
return(S0*(1 -(1 -(1 -C)/S0)^(n*extra)))
}
# Extrapolation des inventaires
eS <- apply(Samples, 2, ExtrapolateS) + S0
# Tirage de nSim communautés de taille n(1+extra)
Communities <- rmultinom(nSim, n*(1 + extra), Ps)
richCommunities <- colSums(Communities > 0)
# Distribution des résultats
deCommunities <- density(richCommunities)
deB <- density(eB)
dei <- density(ei)
deS <- density(eS)
# Figure
Xlab <- "Nombre d'espèces"
Ylab <- "Densité de probabilité"
ggplot(data.frame(richCommunities, eB, ei, eS)) +
geom_density(aes(richCommunities)) +
geom_density(aes(eB), lty = 2, col = "red") +
geom_density(aes(ei), lty = 3, col = "blue") +
geom_density(aes(eS), lty = 4, col = "darkgreen") +
labs(x = Xlab, y = Ylab)Béguinot (2015a) propose également une forme analytique de la SAC extrapolée en combinant l’équation (21.1) à l’estimateur jackknife d’ordre 2. Alors, dans le domaine de validité de l’estimateur jackknife 2, c’est-à-dire quand le nombre de singletons est supérieur à 0,6 fois le nombre de doubletons, la richesse pour \(n\) individus est \[\begin{equation} \tag{21.2} s^{n} = s^{n_0} +2s^{n_0}_{1}-s^{n_0}_{2} -\left(3s^{n_0}_{1}-2s^{n_0}_{2}\right)*\frac{n_0}{n} -\left(s^{n_0}_{2}-s^{n_0}_{1}\right)*\left(\frac{n_0}{n}\right)^2, \end{equation}\] où \(n_0\) est la taille de l’inventaire de départ.
La méthode est testée ici sur la même communauté log-normale. 500 inventaires de 5000 individus sont réalisés et chacun est extrapolé jusqu’à 25000 individus.
# Extrapolation jusqu'à
Nmax <- 25000
# SAC réelle, obtenue par la somme des entropies de Simpson
# généralisées Calcul de p(1-p)^r pour toutes les espèces
# (en lignes) et tous les r (en colonnes)
GSsr <- Ps * sapply(1:Nmax, function(r) (1 - Ps)^r)
# Simpson généralisé pour tous les r
GSr <- colSums(GSsr)
# SAC: somme cumulée des entropies de Simpson généralisées
SAC <- cumsum(GSr)
# Fonction d'extrapolation de la SAC
ExtraSAC <- function(Ns, N) {
# Ns est le vecteur des abondances de l'échantillon, N
# est le vecteur des tailles à extrapoler
n0 <- sum(Ns)
Sn0 <- sum(Ns > 0)
f1 <- sum(Ns == 1)
f2 <- sum(Ns == 2)
# Extrapolation à chaque taille
vapply(N, function(n) Sn0 + 2 * f1 - f2 - (3 * f1 - 2 * f2) *
n0/n - (f2 - f1) * (n0/n)^2, 0)
}
# Taille de l'échantillon
n <- 5000
# Tirage de nSim inventaires dans la communauté log-normale
Samples <- rmultinom(nSim, n, Ps)
# Extrapolation des inventaires
ExtraSACs <- apply(Samples, 2, ExtraSAC, n:Nmax)
# Moyenne et intervalle de confiance à 95%
Moyenne <- apply(ExtraSACs, 1, mean)
Max <- apply(ExtraSACs, 1, quantile, probs = 0.975)
Min <- apply(ExtraSACs, 1, quantile, probs = 0.025)
# Taille d'échantillon réduite
nReduit <- 1000
# Tirage de nSim inventaires dans la communauté log-normale
Samples <- rmultinom(nSim, nReduit, Ps)
# Extrapolation des inventaires
ExtraSACs <- apply(Samples, 2, ExtraSAC, nReduit:Nmax)
# Moyenne
MoyenneReduit <- apply(ExtraSACs, 1, mean)À titre de comparaison, l’extrapolation d’un seul inventaire de 1000 individus est également tentée.
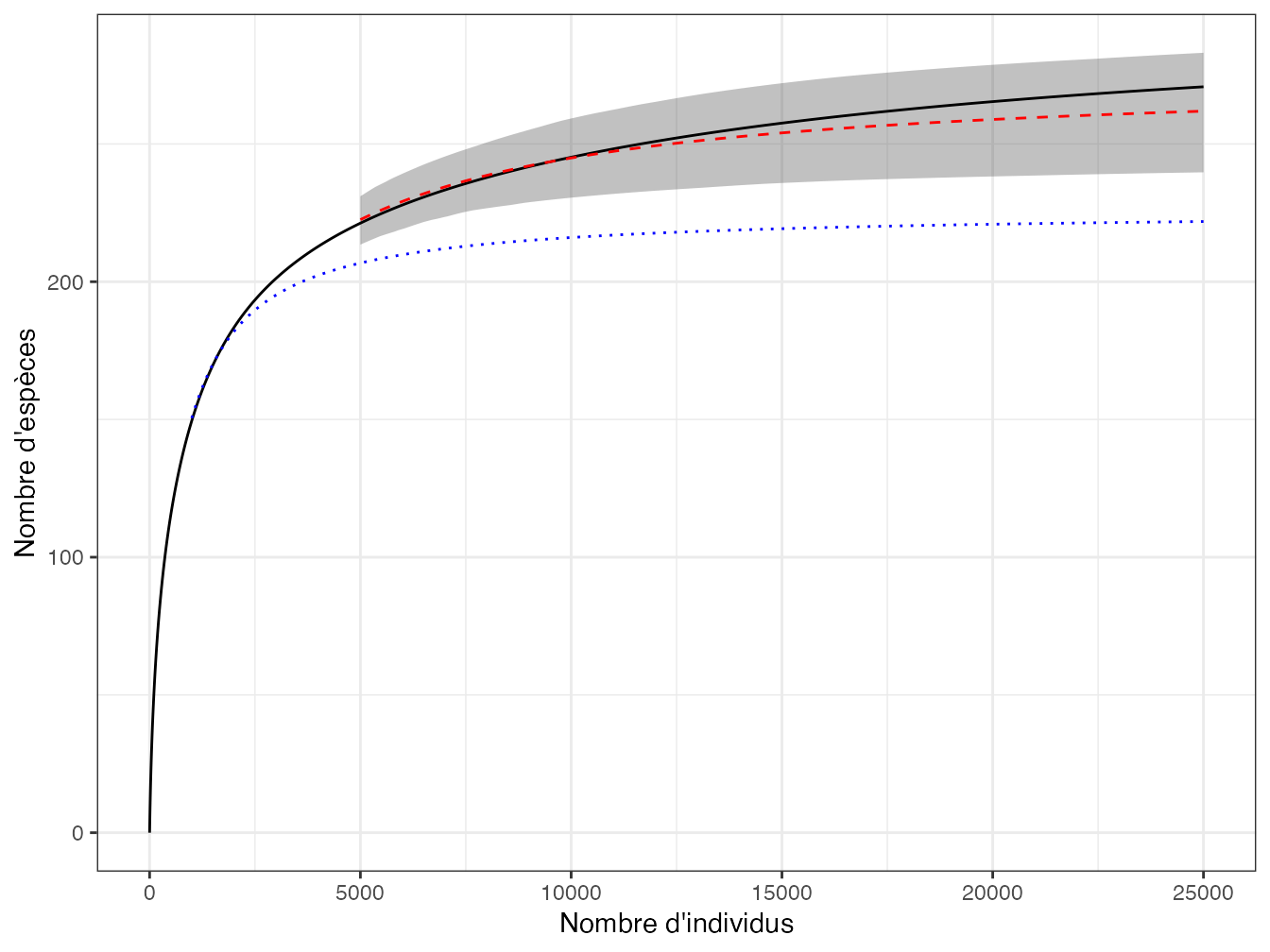
Figure 21.5: Extrapolation de 500 inventaires de 5000 individus (valeurs moyenne en tireté rouge et enveloppe de confiance à 95 % en gris) superposée à la SAC réelle d’une communauté log-normale de 300 espèces. L’extrapolation (en pointillés bleu) d’un inventaire limité à 1000 individus est sévèrement sous-estimée.
L’extrapolation fonctionne assez bien (figure 21.5) tant que l’échantillonnage n’est pas trop faible. Avec un inventaire de 5000 individus dans cet exemple, l’estimation de la richesse asymptotique par l’estimateur jackknife 2 est correcte, l’extrapolation de la SAC l’est aussi. En limitant l’inventaire à 1000 individus, l’information disponible est trop limitée.
Le code R nécessaire pour réaliser la figure est :
ggplot() +
geom_ribbon(aes(x, ymin = Min, ymax = Max),
data.frame(x = n:Nmax, Min, Max), alpha = 0.3) +
geom_line(aes(x, y), data.frame(x = 0:Nmax, y = c(0, SAC))) +
geom_line(aes(x, y), data.frame(x = n:Nmax, y = Moyenne),
col = "red", lty = 2) +
geom_line(aes(x, y), data.frame(x = nReduit:Nmax, y = MoyenneReduit),
col = "blue", lty = 3) +
labs(x = "Nombre d'individus", y = "Nombre d'espèces")21.3 Influence de la structure spatiale
Les modèles classiques de courbes aire-espèces supposent un tirage indépendant des individus. Sur le terrain, par exemple en forêt, l’échantillonnage est continu : s’il existe une structure spatiale comme des agrégats, la probabilité que l’arbre suivant soit d’une espèce donnée dépend de ses voisins, donc de l’arbre précédent. Intuitivement, on comprend bien que le nouvel arbre de la même espèce apporte moins d’information, ce qui revient à surestimer la taille de l’échantillon ou sous-estimer la richesse pour une taille d’échantillon fixée (Veech 2005).
Plotkin, Potts, Leslie, et al. (2000) traitent un problème un peu différent : connaissant le nombre total d’espèces dans les dispositifs de la figure 22.2, ils tracent la courbe de raréfaction théorique qui considère simplement que la probabilité de ne pas rencontrer une espèce suit une loi binomiale, les tirages étant indépendants. Ce modèle surestime largement la diversité pour les petites surfaces : la probabilité de ne pas rencontrer une espèce agrégative est sous-estimée. Le biais diminue quand la surface d’échantillonnage augmente, parce que la taille relative des agrégats diminue.
Les effets de l’agrégation peuvent donc être opposés selon la question posée. Dans tous les cas, il suffit de considérer qu’un agrégat surestime le nombre d’arbres de son espèce qui devrait être pris en compte dans le cadre d’un modèle à tirages indépendants.
Plotkin et al. proposent une méthode permettant de prendre en compte la structure spatiale pour fournir des modèles de courbes aire-espèces fiables, dans un cadre particulier où le nombre total d’espèces et leur structure spatiale sont connus. La méthode nécessite une carte des individus. Le semis de point est considéré comme le résultat d’un processus de Neyman-Scott (Neyman et Scott 1958) : des centres d’agrégats sont tirés de façon complètement aléatoire et les individus sont répartis autour des centres selon une loi normale en deux dimensions. Les paramètres du processus sont estimés à partir du semis de points, puis la courbe aire-espèces est obtenue par simulation du processus.
Le problème est traité de façon plus approfondie par Picard, Karembe, et Birnbaum (2004) qui s’appuient sur la théorie des processus ponctuels. En supposant que la distribution spatiale des espèces est homogène (c’est-à-dire stationnaire et isotrope), la forme du domaine échantillonné n’a pas d’importance : l’aire \(A\) peut être représentée par un cercle de rayon \(r=\sqrt{{A}/{\pi}}\). La probabilité d’observer l’espèce \(s\) dans \(A\) est identique à la probabilité que la distance entre un individu de l’espèce \(s\) et un point arbitrairement choisi soit inférieure à \(r\). Cette probabilité a été largement étudiée et est connue sous le nom de fonction \(F\) de Diggle (1983), ou empty space function. \(F_s(r)\) est la fonction d’espace vide de l’espèce \(s\), dont l’argument est la distance \(r\). Le nombre d’espèces peut être écrit comme la somme des fonctions \(F_s\) :
\[\begin{equation} \tag{21.3} {\mathbb E}\left( S^A \right) = \sum_s{F_s\left( r \right) }. \end{equation}\]
La fonction \(F_s(r)\) est connue pour les processus ponctuels courants (N. A. Cressie 1993; Stoyan et Stoyan 1994). Le processus de Poisson place les individus indépendamment les uns des autres avec la même probabilité partout. Son seul paramètre est l’intensité \(\lambda_s\), qui donne l’espérance du nombre d’individus de l’espèce \(s\) par unité de surface. Si toutes les espèces sont distribuées selon un processus de Poisson, la courbe aire-espèce est décrite par
\[\begin{equation} \tag{21.4} {\mathbb E}\left( S^A \right) = S - \sum_s{e^{-\lambda_s A}}. \end{equation}\]
L’équation (21.4) est identique au modèle de distribution aléatoire de Coleman en remplaçant la distribution observée des effectifs par espèce par l’intensité du processus de Poisson.
Les formes de \(F_s\) sont connues aussi pour des processus agrégatifs, notamment le processus de Matérn (1960) ou des distributions régulières.
La courbe aire-espèce peut donc être évaluée à partir d’inventaires fournissant la position des individus.
Le processus ponctuel correspondant à chaque espèce peut être inféré pour fournir une forme analytique de la courbe comme dans l’équation (21.4) ou bien la fonction d’espace vide de chaque espèce peut être estimée à partir des données par la fonction Fest du package spatstat et sommée pour toutes les espèces selon l’équation (21.3).
La relation aire-espèce contient au moins autant de paramètres que d’espèces : l’intensité \(\lambda_s\) si l’espèce \(s\) est distribuée spatialement selon un processus de Poisson, deux paramètres supplémentaires pour le processus de Matérn. Cette complexité peut être réduite si la distribution des fréquences des espèces (la SAD) est connue. Picard et al. fournissent les relations pour une SAD en log-séries et une SAD géométrique, avec une distribution spatiale suivant un processus de Poisson : elles ne contiennent que deux paramètres, un lié au nombre total d’individus, et un propre à chaque SAD. Les formules se compliquent quand la distribution spatiale n’est pas poissonnienne et ne sont pas disponibles quand la SAD (log-normale par exemple) ne prévoit pas le nombre exact d’individus par espèce.
Enfin, il est possible de prendre en compte les espèces non observées. La relation aire-espèce (21.3) s’entend pour toutes les espèces. Elle peut être réécrite sous la forme \[\begin{equation} \tag{21.5} {\mathbb E}\left( S^A \right) = \sum_{s=1}^{S_{\ne 0}}{F_s\left( r \right)} + \sum_{s=S_{\ne 0}+1}^{S}{F_s\left( r \right)}. \end{equation}\]
Le premier terme de la somme correspond aux espèces observées, le deuxième aux espèces non observées. La distribution des espèces non observées peut maintenant être estimée dans certains cas (Chao, Hsieh, et al. 2015) et leur distribution spatiale être supposée poissonnienne puisque ce sont des espèces rares (Picard, Karembe, et Birnbaum 2004), ce qui ouvre la voie à une meilleure estimation de la courbe.