6 Cadre

La diversité fonctionnelle ou phylogénétique prend en compte la proximité des espèces entre elles. Généralement, la distance entre espèces est évaluée dans l’espace des traits, approximation de l’espace des niches, pour la diversité fonctionnelle et dans un dendrogramme représentant la phylogénie ou la taxonomie pour la diversité phylogénétique.

Les mesures neutres de la diversité considèrent que toutes les classes auxquelles les objets appartiennent sont différentes, sans que certaines soient plus différentes que d’autres. Par exemple, toutes les espèces sont équidistantes les unes des autres, qu’elles appartiennent au même genre ou à des familles différentes. Intuitivement, l’idée qu’une communauté de \(S\) espèces toutes de genres différents est plus diverse qu’une communauté de \(S\) espèces du même genre est satisfaisante. B. H. Walker (1992) argumente en faveur de la protection de groupes fonctionnels plutôt que de celle de chacune des espèces qui les constitue pour maintenir le bon état des écosystèmes.

Il s’agit donc de caractériser la différence entre deux classes d’objets, puis de construire des mesures de diversité en rapport (Pielou 1975; May 1990; Cousins 1991). En écologie, ces différences sont fonctionnelles ou phylogénétiques, définissant la diversité fonctionnelle (Tilman et al. 1997) ou la diversité phylogénétique (phylodiversity) (Webb, Losos, et Agrawal 2006).

Les premières propositions de ce type d’indices sont dues à Rao (1982) (voir section 7.6) puis, avec nettement moins de succès, Vane-Wright, Humphries, et Williams (1991) et Warwick et Clarke (1995). Chave, Chust, et Thébaud (2007) montrent que la diversité neutre prédit mal la diversité phylogénétique (calculée par l’entropie quadratique de Rao).

De nombreuses mesures de diversité ont été créées et plusieurs revues permettent d’en faire le tour. (Ricotta 2007; Vellend et al. 2010) Les mesures présentées ici sont les plus utilisées, et notamment celles qui peuvent être ramenées aux mesures classiques en fixant une distance égale entre toutes les espèces. Le cadre méthodologique dans lequel ces mesures ont été développées est présenté dans ce chapitre, suivi par une revue des nombreuses mesures de diversité fonctionnelles et phylogénétiques de la littérature. L’entropie phylogénétique et la diversité de Leinster et Cobbold sont ensuite développées en détail, suivies d’une synthèse et de considérations sur la mesure de la diversité individuelle plutôt que spécifique.

Des exemples montrent comment calculer cette diversité, principalement à l’aide du package entropart. Le package contient les données d’inventaire de deux hectares du dispositif de Paracou et la taxonomie des espèces concernées :

library("entropart")
# Chargement du jeu de données
data(Paracou618)

6.1 Dissimilarité et distance

Une similarité ou dissimilarité est toute application à valeurs numériques qui permet de mesurer le lien entre les individus d’un même ensemble ou entre les variables. Pour une similarité le lien est d’autant plus fort que sa valeur est grande.

Une dissimilarité vérifie (\(k\), \(l\) et \(m\) sont trois individus) :

• La dissimilarité d’un individu avec lui-même est nulle : \(d\left(k,k\right)=0\) ;
• La dissimilarité entre deux individus différents est positive : \(d\left(k,l\right)\ge 0\) ;
• La dissimilarité est symétrique : \(d\left(k,l\right)=d\left(l,k\right)\).

Une distance vérifie en plus :

• La distance entre deux individus différents est strictement positive : \(d\left(k,l\right)=0\Rightarrow k=l\) ;
• L’inégalité triangulaire : \(d\left(k,m\right)\le d\left(k,l\right)+d\left(l,m\right)\). De nombreux indices de dissimilarité ne vérifient pas cette propriété.

Une distance est euclidienne si elle peut être représentée par des figures géométriques. On peut rendre toute distance euclidienne par ajout d’une constante (Lingoes 1971; Cailliez 1983). Dans R, utiliser is.euclid() pour vérifier qu’une distance est euclidienne, et cailliez() ou lingoes() pour la transformation.

Enfin, une distance est ultramétrique si \(d\left(k,m\right) \le \max\left(d\left(k,l\right),d\left(l,m\right)\right)\). Les distances obtenues en mesurant les longueurs des branches d’un dendrogramme (arbre) résultant d’une classification hiérarchique sont ultramétriques.

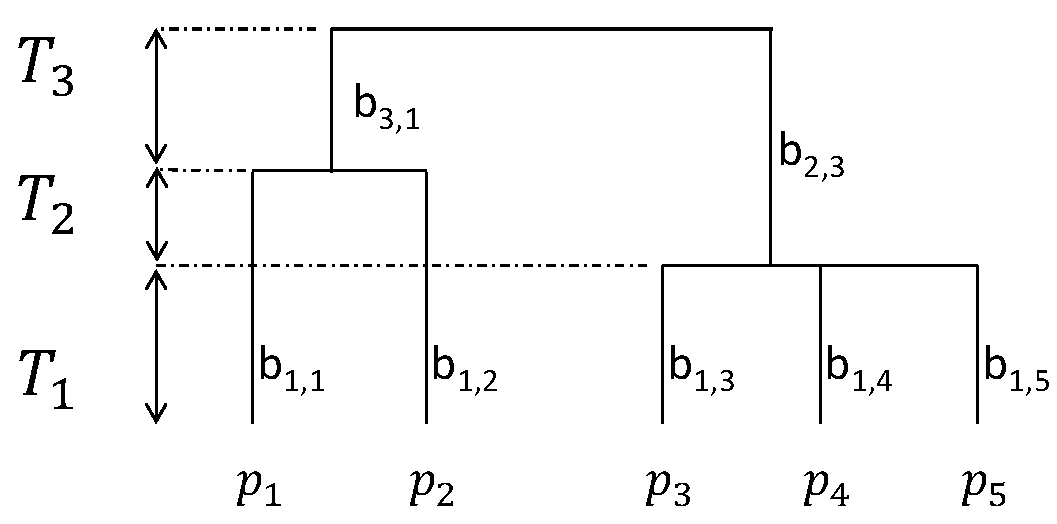
Figure 6.1: Arbre phylogénétique ou fonctionnel hypothétique. 5 espèces sont présentes (\(S=5\)), leurs probabilités notées \(p_1\) à \(p_5\). Les noms des branches sont affichés.

La façon exacte de mesurer les longueurs de branche est illustrée par la figure 6.1 : la distance entre les espèces 1 et 2 est \(T_1+T_2\), elle est égale à \(T_1\) entre les espèces 4 et 5. La distance est la hauteur du premier noeud commun.

6.2 Distance phylogénétique

La façon la plus évidente de définir une distance entre espèces est d’utiliser la taxonomie (Clarke et Warwick 2001, Warwick2001), en attribuant une distance arbitraire (par exemple 1) à deux espèces du même genre, une autre (par exemple 2) à deux espèces de la même famille, etc. La distance définie est ultramétrique.

La taxonomie peut être remplacée avantageusement par une phylogénie. La phylogénie idéale contiendrait l’histoire évolutive de toutes les espèces et les distances seraient les temps de divergence depuis le premier ancêtre commun. En pratique, les phylogénies sont établies à partir d’un nombre de marqueurs génétiques limités, sans datation précise (mais avec des calages partiels à partir de fossiles), et ne sont pas toujours ultramétriques. Elles peuvent prendre en compte chaque individu, sans regroupement par espèce. Une méthode pour dater une phylogénie est fournie par Chave, Chust, et Thébaud (2007) Zanne et al. (2014) fournissent une phylogénie datée de plus de 32000 espèces. Ricotta et al. (2012) montrent sur des exemples que la diversité calculée à partir de phylogénies datées est très corrélée à celle calculée à partir de simples taxonomies.

Dans tous les cas, la distance est une mesure de la divergence évolutive. Du point de vue de la biologie de la conservation, chaque espèce accumule une quantité d’évolution, interprétée comme une quantité d’information (Crozier 1997) dont le maximum doit être préservé.

L’entropie phylogénétique (voir chapitre 8) utilise un arbre phylogénétique pour mesurer la diversité.

6.3 Distance fonctionnelle

L’approche fonctionnelle est différente. Chaque espèce ou individu est représenté par ses valeurs de traits dans un espace multidimensionnel. Le vecteur de traits est considéré comme un proxy de la niche écologique (Westoby et al. 2002). Les individus proches dans l’espace des traits sont donc considérés comme proches écologiquement. Les distances entre les points peuvent être calculées directement dans l’espace des traits ou, fréquemment, un arbre est construit par classification automatique hiérarchique.

La première étape consiste donc à choisir un ensemble de traits pertinents et à les mesurer de façon standardisée (Cornelissen et al. 2003). Toute la stratégie relative à la photosynthèse peut être par exemple assez bien résumée par la masse surfacique des feuilles (I. J. Wright et al. 2004), mais, en forêt tropicale, ce trait est décorrélé de la densité du bois (Baraloto et al. 2010). Les valeurs manquantes peuvent être complétées en utilisant toute l’information disponible par MICE (multiple imputation by chained equations) (van Buuren et al. 2006), disponible sous R dans le package mice (van Buuren et Groothuis-Oudshoorn 2011).

La prise en compte de variables qualitatives ou de rang et la possibilité de données manquantes pose un problème pratique de construction de la matrice de dissimilarité, traité par Gower (1971). La formule de Gower, étendue par Podani (1999) puis Pavoine et al. (2009) à d’autres types de variables, calcule la dissimilarité entre deux espèces par la moyenne des dissimilarités calculées pour chaque trait, dont la valeur est comprise entre 0 et 1 :

• Pour une variable quantitative, la différence de valeur entre deux espèces est normalisée par l’étendue des valeurs de la variable ;
• Les variables ordonnées sont remplacées par leur rang et traitées comme les variables quantitatives ;
• Pour des variables qualitatives, la dissimilarité vaut 0 ou 1 ;
• Les valeurs manquantes sont simplement ignorées et n’entrent pas dans la moyenne.

Une matrice de distances entre espèces est construite de cette façon. Podani et Schmera (2006) suggèrent d’utiliser ensuite une classification hiérarchique par UPGMA (Sokal et Michener 1958) qu’ils montrent être la plus robuste (pour le calcul de FD, voir section 7.5) à l’ajout ou au retrait d’un trait ou d’une espèce. Mouchet et al. (2008) suggèrent plutôt d’appliquer toutes les méthodes de classification et de retenir à la fin l’arbre dont la distribution des distances entre espèces dans l’arbre est la plus proche de la distribution des distances dans la matrice de dissimilarités : cette proximité est mesurée par la corrélation cophénétique, c’est-à-dire le coefficient de corrélation entre les valeurs de distances (Sokal et Rohlf 1962; Legendre et Legendre 2012). Un arbre consensus (Felsenstein 2004) est souvent plus proche de la matrice de distance.

Un dendrogramme fonctionnel n’a pas d’interprétation aussi claire qu’un arbre phylogénétique qui représente le processus de l’évolution. Il peut être interprété comme la représentation à des échelles de plus en plus grossières en allant vers le haut de l’arbre de regroupements fonctionnels dans des niches de plus en plus vastes.

La transformation d’une matrice (non ultramétrique) en dendrogramme déforme la topologie des espèces (Pavoine, Ollier, et Dufour 2005; Podani et Schmera 2007) : une mesure de diversité qui utilise directement la matrice est préférable, c’est un intérêt de la diversité de Leinster et Cobbold (voir chapitre 9). Maire et al. (2015) ont défini une mesure de qualité d’un espace fonctionnel, mSD, comme l’écart quadratique moyen entre les distances fonctionnelles entre espèces dans l’espace utilisé (par exemple les distances cophénétiques dans un dendrogramme fonctionnel) et les distances originales (dans la matrice de distance à partir de laquelle l’arbre a été obtenu). Dans la matrice originale, les valeurs de traits sont centrées et réduites, et la hauteur du dendrogramme est fixée pour que la distance cophénétique maximale soit égale à la distance originale maximale.

Villéger, Maire, et Leprieur (2017) ont montré que l’utilisation de dendrogrammes fonctionnels dans une étude de Sobral, Lees, et Cianciaruso (2016) amène à sous-estimer les changements de niveau de biodiversité liés à l’arrivée d’espèces invasives d’oiseaux. Dans la très grande majorité des dendrogrammes utilisés, la transformation de la matrice de distance a entraîné un écart moyen de plus de 10 % par rapport aux valeurs originales (une valeur de mSD, l’écart quadratique moyen, supérieure à 1 %) Cette déformation est suffisante pour largement invalider les résultats obtenus.

6.4 Équivalence des deux diversités

L’approche fonctionnelle étant particulièrement complexe et lourde à mettre en oeuvre (notamment pour la mesure des traits sur chaque individu), la tentation a été grande de considérer que la phylogénie contenait plus d’information fonctionnelle que ce qui pouvait être mesuré, et donc de considérer la diversité phylogénétique comme proxy de la diversité fonctionnelle.

Du point de vue théorique, le modèle le plus simple de l’évolution de la valeur d’un trait hypothétique au cours du temps est le mouvement brownien : à chaque génération, la valeur du trait varie un peu, sans mémoire. Dans ce cadre (Felsenstein 1985), la variance de la valeur actuelle du trait pour une espèce donnée est proportionnelle à la durée de l’évolution et la covariance entre deux espèces à celle de l’âge de leur ancêtre commun. Deux espèces proches dans l’arbre phylogénétique décrivant l’évolution doivent donc avoir des valeurs de trait corrélées.

Webb (2000) a montré que des communautés d’arbres tropicaux avaient une moins grande diversité phylogénétique locale qu’attendue sous l’hypothèse nulle d’une distribution aléatoire des espèces, et a supposé que la cause en était le filtrage environnemental local, agissant sur les traits et observables par la phylogénie, sous l’hypothèse de conservation phylogénétique des traits fonctionnels. La discipline appelée écologie phylogénétique des communautés cherche encore à comprendre quels traits sont conservés et lesquels sont convergents (Cavender-Bares et al. 2009).

Swenson et Enquist (2009) puis Hähn et al. (2024) ont montré que la corrélation entre les deux diversités était faible, voire négative. L’utilisation de la diversité phylogénétique comme proxy de la diversité fonctionnelle n’est pas satisfaisante (Pavoine et Bonsall 2011). Pour optimiser la conservation, les deux aspects de la diversité, souvent divergents, doivent être pris en compte (Devictor et al. 2010).

6.5 Typologie des mesures

À partir de la littérature (Ricotta 2007; Pavoine et Bonsall 2011), une typologie des mesures de diversité émerge. Elle étend les notions classiques de richesse et équitabilité.

La richesse est l’accumulation de classes différentes dans les mesures classiques. Dans un arbre phylogénétique, la longueur des branches représente un temps d’évolution : la richesse en est la somme. FD et PD sont des mesures de richesse.

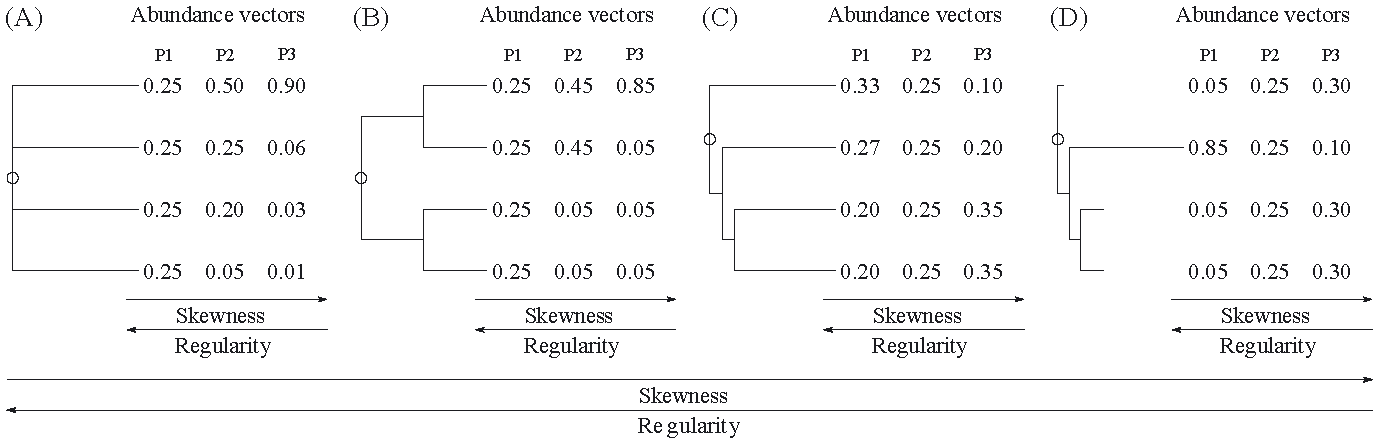
Figure 6.2: Régularité contre irrégularité. Les arbres de A à D sont de plus en plus irréguliers. L’arbre A, parfaitement régulier, est le cadre des mesures classiques de la diversité. La phylogénie étant donnée, trois vecteurs d’abondance (P1 à P3) sont de moins en moins réguliers : dans les cas C et D, la régularité maximale n’est pas obtenue pour des effectifs identiques, mais en augmentant les effectifs des espèces originales.

La régularité mesure la façon dont les espèces occupent uniformément l’espace des niches (Pavoine et Bonsall 2011). Cette notion est simple dans un espace multidimensionnel (par exemple, l’espace des traits fonctionnels). Dans un arbre phylogénétique (figure 6.2, Pavoine et Bonsall (2011)), la régularité de l’arbre (Mooers et Heard 1997) est un premier critère, complété éventuellement par les abondances. Dans un arbre parfaitement régulier, la régularité se réduit à l’équitabilité.

Les mesures de divergence sont des fonctions croissantes de la dissimilarité entre les espèces, généralement considérées par paires. Certaines sont pondérées par les abondances, d’autres non. Dans un arbre parfaitement régulier, l’indice de Simpson est une mesure de divergence pondérée. Ces mesures sont influencées par la richesse et la régularité.

Face à la profusion des mesures de diversité fonctionnelle, Ricotta (2005a), en complément de Solow et Polasky (1994) établit un certain nombre d’axiomes :

1. Monotonicité d’ensemble : la diversité ne doit pas diminuer quand une espèce est ajoutée avec une faible probabilité (qui ne modifie pas la structure de la communauté existante), quelles que soient ses caractéristiques fonctionnelles ;
2. Jumelage (Weitzman 1992) : l’introduction d’une espèce identique à une espèces existante ne doit pas augmenter la diversité. De façon moins triviale, une espèce infiniment proche ne doit pas augmenter la diversité : il s’agit donc d’un axiome de continuité dans l’espace des niches.
3. Monotonicité de distance : la diversité ne doit pas diminuer quand la distance entre espèces est augmentée.
4. Décomposabilité : les mesures de divergence doivent être décomposables en diversité \(\alpha\), \(\beta\) et \(\gamma\), ce qui implique leur concavité par rapport aux probabilités.

L’entropie phylogénétique permet d’unifier ces notions, mais de nombreuses mesures ont été proposées. Elles sont détaillées au chapitre suivant.