Shannon entropy of a community

Calculates the Shannon entropy of a probability vector.

Shannon(NorP, ...)
bcShannon(Ns, Correction = "Best", CheckArguments = TRUE)
# S3 method for ProbaVector
Shannon(NorP, ..., CheckArguments = TRUE, Ps = NULL)
# S3 method for AbdVector
Shannon(NorP, Correction = "Best", Level = NULL,
  PCorrection = "Chao2015", Unveiling = "geom", RCorrection = "Rarefy", ..., 
  CheckArguments = TRUE, Ns = NULL)
# S3 method for integer
Shannon(NorP, Correction = "Best", Level = NULL,
  PCorrection = "Chao2015", Unveiling = "geom", RCorrection = "Rarefy", ..., 
  CheckArguments = TRUE, Ns = NULL)
# S3 method for numeric
Shannon(NorP, Correction = "Best", Level = NULL, 
  PCorrection = "Chao2015", Unveiling = "geom", RCorrection = "Rarefy", ..., 
  CheckArguments = TRUE, Ps = NULL, Ns = NULL)

Arguments

Ps: A probability vector, summing to 1.
Ns: A numeric vector containing species abundances.
NorP: A numeric vector, an integer vector, an abundance vector (AbdVector) or a probability vector (ProbaVector). Contains either abundances or probabilities.
Correction: A string containing one of the possible asymptotic estimators: "None" (no correction), "ChaoShen", "GenCov", "Grassberger", "Grassberger2003", "Schurmann", "Holste", "Bonachela", "Miller", "ZhangHz", "ChaoJost", "Marcon", "UnveilC", "UnveiliC", "UnveilJ" or "Best", the default value. Currently, "Best" is "UnveilJ".
Level: The level of interpolation or extrapolation. It may be an a chosen sample size (an integer) or a sample coverage (a number between 0 and 1). Entropy extrapolation require its asymptotic estimation depending on the choice of Correction. Entropy interpolation relies on the estimation of Abundance Frequence Counts: then, Correction is passed to AbdFreqCount as its Estimator argument.
PCorrection: A string containing one of the possible corrections to estimate a probability distribution in as.ProbaVector: "Chao2015" is the default value. Used only for extrapolation.
Unveiling: A string containing one of the possible unveiling methods to estimate the probabilities of the unobserved species in as.ProbaVector: "geom" (the unobserved species distribution is geometric) is the default value. If "None", the asymptotic distribution is not unveiled and only the asymptotic estimator is used. Used only for extrapolation.
RCorrection: A string containing a correction recognized by Richness to evaluate the total number of species in as.ProbaVector. "Rarefy" is the default value to estimate the number of species such that the entropy of the asymptotic distribution rarefied to the observed sample size equals the observed entropy of the data. Used only for extrapolation.
...: Additional arguments. Unused.
CheckArguments: Logical; if TRUE, the function arguments are verified. Should be set to FALSE to save time when the arguments have been checked elsewhere.

Details

Bias correction requires the number of individuals to estimate sample Coverage.

Correction techniques are from Miller (1955), Chao and Shen (2003), Grassberger (1988), Grassberger (2003), Schurmann (2003), Holste et al. (1998), Bonachela et al. (2008), Zhang (2012), Chao, Wang and Jost (2013). More estimators can be found in the entropy package.

Using MetaCommunity mutual information, Chao, Wang and Jost (2013) calculate reduced-bias Shannon beta entropy (see the last example below) with better results than the Chao and Shen estimator, but community weights cannot be arbitrary: they must be proportional to the number of individuals.

The functions are designed to be used as simply as possible. Shannon is a generic method. If its first argument is an abundance vector, an integer vector or a numeric vector which does not sum to 1, the bias corrected function bcShannon is called.

Entropy can be estimated at a specified level of interpolation or extrapolation, either a chosen sample size or sample coverage (Chao et al., 2014), rather than its asymptotic value. Extrapolation relies on the estimation of the asymptotic entropy. If Unveiling is "None", then the asymptotic estimation of entropy is made using the chosen Correction, else the asymtpotic distribution of the community is derived and its estimated richness adjusted so that the entropy of a sample of this distribution of the size of the actual sample has the entropy of the actual sample.

Value

A named number equal to the calculated entropy. The name is that of the bias correction used.

References

Bonachela, J. A., Hinrichsen, H. and Munoz, M. A. (2008). Entropy estimates of small data sets. Journal of Physics A: Mathematical and Theoretical 41(202001): 1-9.

Chao, A. and Shen, T. J. (2003). Nonparametric estimation of Shannon's index of diversity when there are unseen species in sample. Environmental and Ecological Statistics 10(4): 429-443.

Chao, A., Wang, Y. T. and Jost, L. (2013). Entropy and the species accumulation curve: a novel entropy estimator via discovery rates of new species. Methods in Ecology and Evolution 4(11):1091-1100.

Chao, A., Gotelli, N. J., Hsieh, T. C., Sander, E. L., Ma, K. H., Colwell, R. K., Ellison, A. M (2014). Rarefaction and extrapolation with Hill numbers: A framework for sampling and estimation in species diversity studies. Ecological Monographs, 84(1): 45-67.

Grassberger, P. (1988). Finite sample corrections to entropy and dimension estimates. Physics Letters A 128(6-7): 369-373.

Grassberger, P. (2003). Entropy Estimates from Insufficient Samplings. ArXiv Physics e-prints 0307138.

Holste, D., Grosse, I. and Herzel, H. (1998). Bayes' estimators of generalized entropies. Journal of Physics A: Mathematical and General 31(11): 2551-2566.

Miller, G. (1955) Note on the bias of information estimates. In: Quastler, H., editor. Information Theory in Psychology: Problems and Methods: 95-100.

Shannon, C. E. (1948). A Mathematical Theory of Communication. The Bell System Technical Journal 27: 379-423, 623-656.

Schurmann, T. (2004). Bias analysis in entropy estimation. Journal of Physics A: Mathematical and Theoretical 37(27): L295-L301.

Tsallis, C. (1988). Possible generalization of Boltzmann-Gibbs statistics. Journal of Statistical Physics 52(1): 479-487.

Zhang, Z. (2012). Entropy Estimation in Turing's Perspective. Neural Computation 24(5): 1368-1389.

Examples

# Load Paracou data (number of trees per species in two 1-ha plot of a tropical forest)
data(Paracou618)
# Ns is the total number of trees per species
Ns <- as.AbdVector(Paracou618.MC$Ns)
# Species probabilities
Ps <- as.ProbaVector(Paracou618.MC$Ns)
# Whittaker plot
plot(Ns)


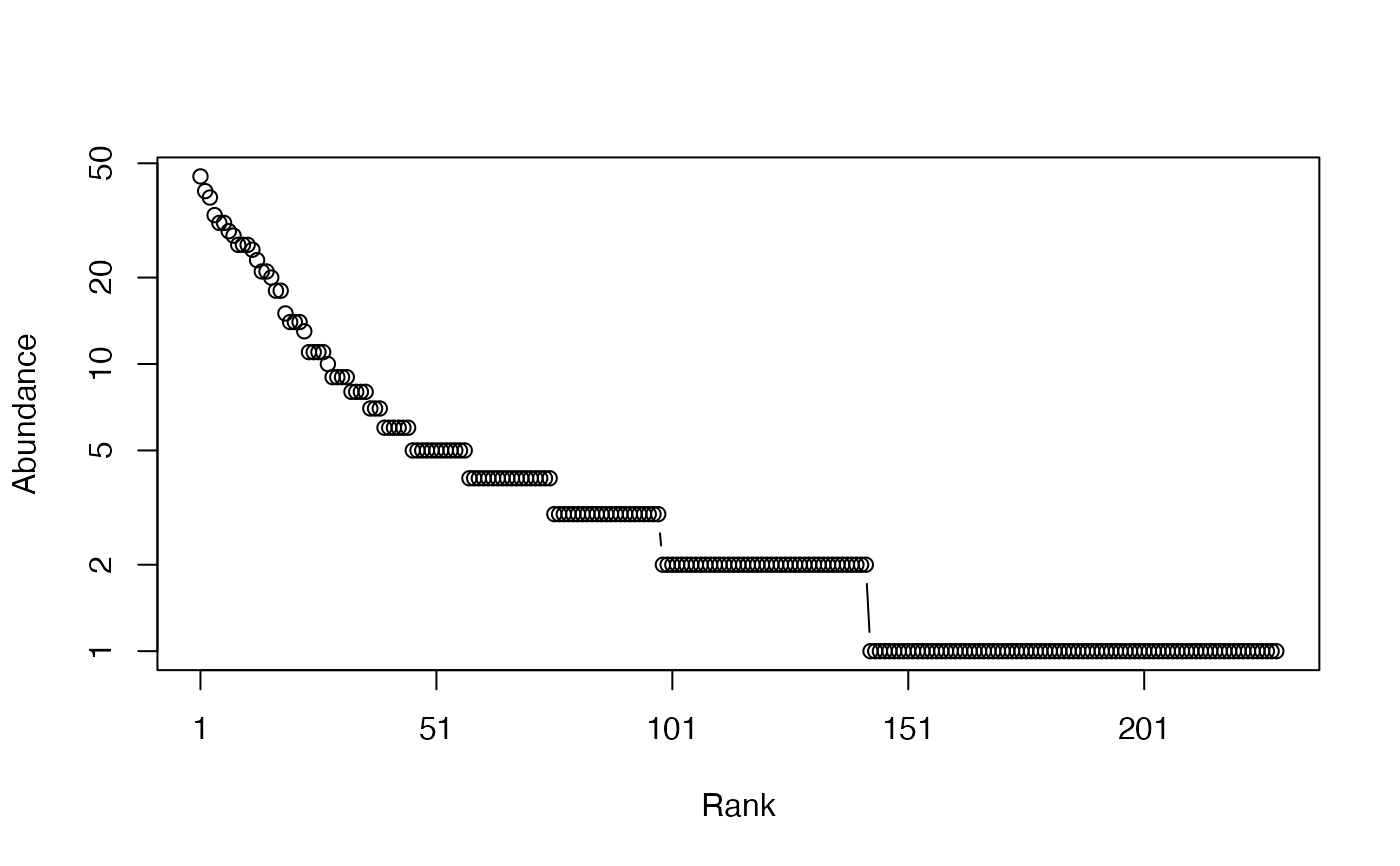# Calculate Shannon entropy
Shannon(Ps)
#>     None 
#> 4.736023 

# Calculate the best estimator of Shannon entropy
Shannon(Ns)
#>  UnveilJ 
#> 4.928035 

# Use metacommunity data to calculate reduced-bias Shannon beta as mutual information
(bcShannon(Paracou618.MC$Ns) + bcShannon(colSums(Paracou618.MC$Nsi))
- bcShannon(Paracou618.MC$Nsi))
#>   UnveilJ 
#> 0.3439827

Arguments

Details

Value

References

See also

Examples