Skip to contents

dbmss

Distance-Based Measures of Spatial Structures

Source: vignettes/dbmss.Rmd
dbmss.Rmd

The dbmss package allows simple computation of spatial statistic functions of distance to characterize the spatial structures of mapped objects, including classical ones (Ripley’s K and others) and more recent ones used by spatial economists (Duranton and Overman’s KdK_d, Marcon and Puech’s MM). It relies on spatstat for some core calculation.

This vignette contains a quick introduction.

Data

The main data format is wmppp for weighted, marked point pattern. It inherits from the ppp class of the spatstat package.

A wmppp object can be created from the coordinates of points, their type and their weight.

library("dbmss")
# Draw the coordinates of 10 points
X <- runif(10)
Y <- runif(10)
# Draw the point types.
PointType <- sample(c("A", "B"), size = 10, replace = TRUE)
# Plot the point pattern. Weights are set to 1 ant the window is adjusted
autoplot(wmppp(data.frame(X, Y, PointType)))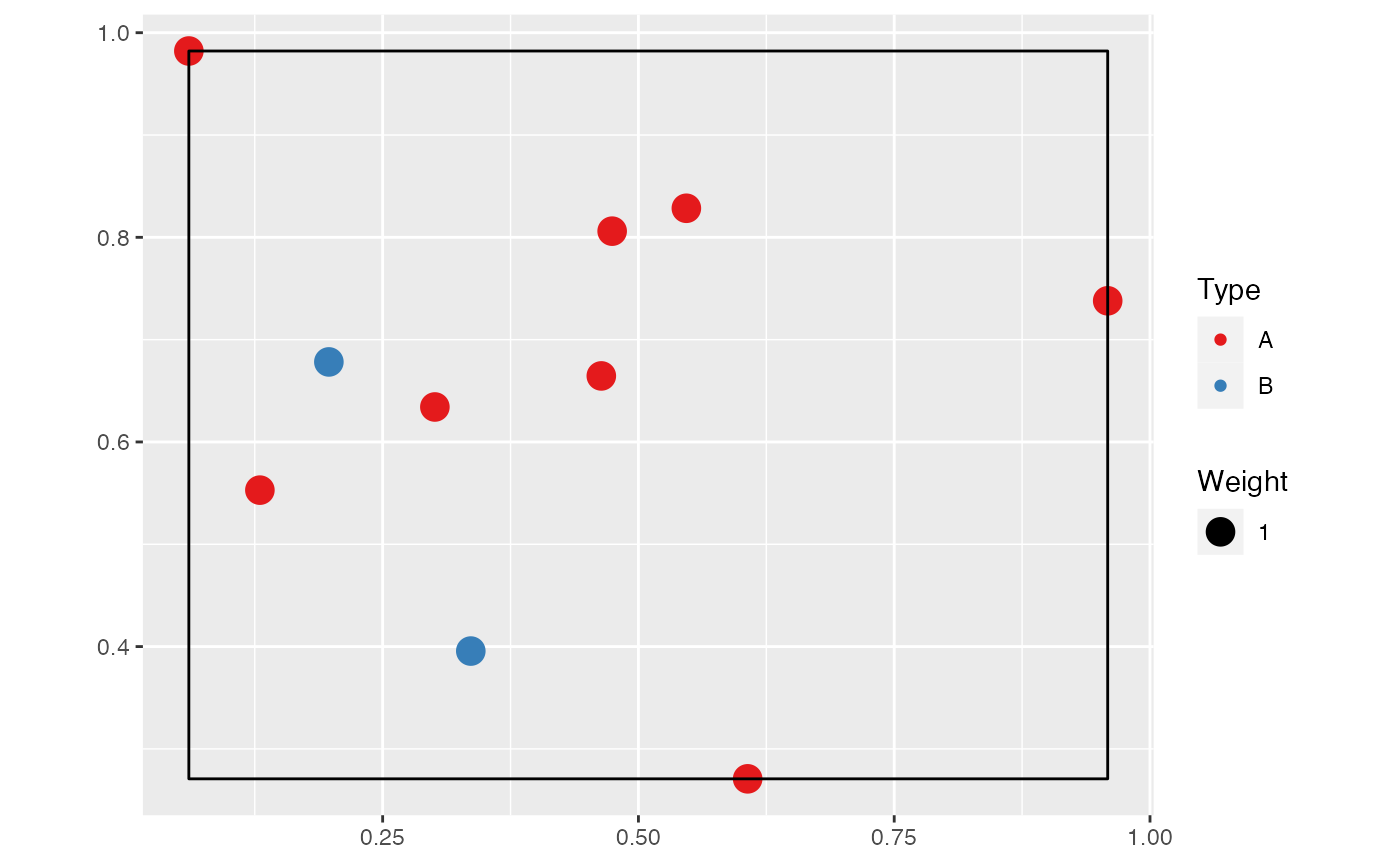

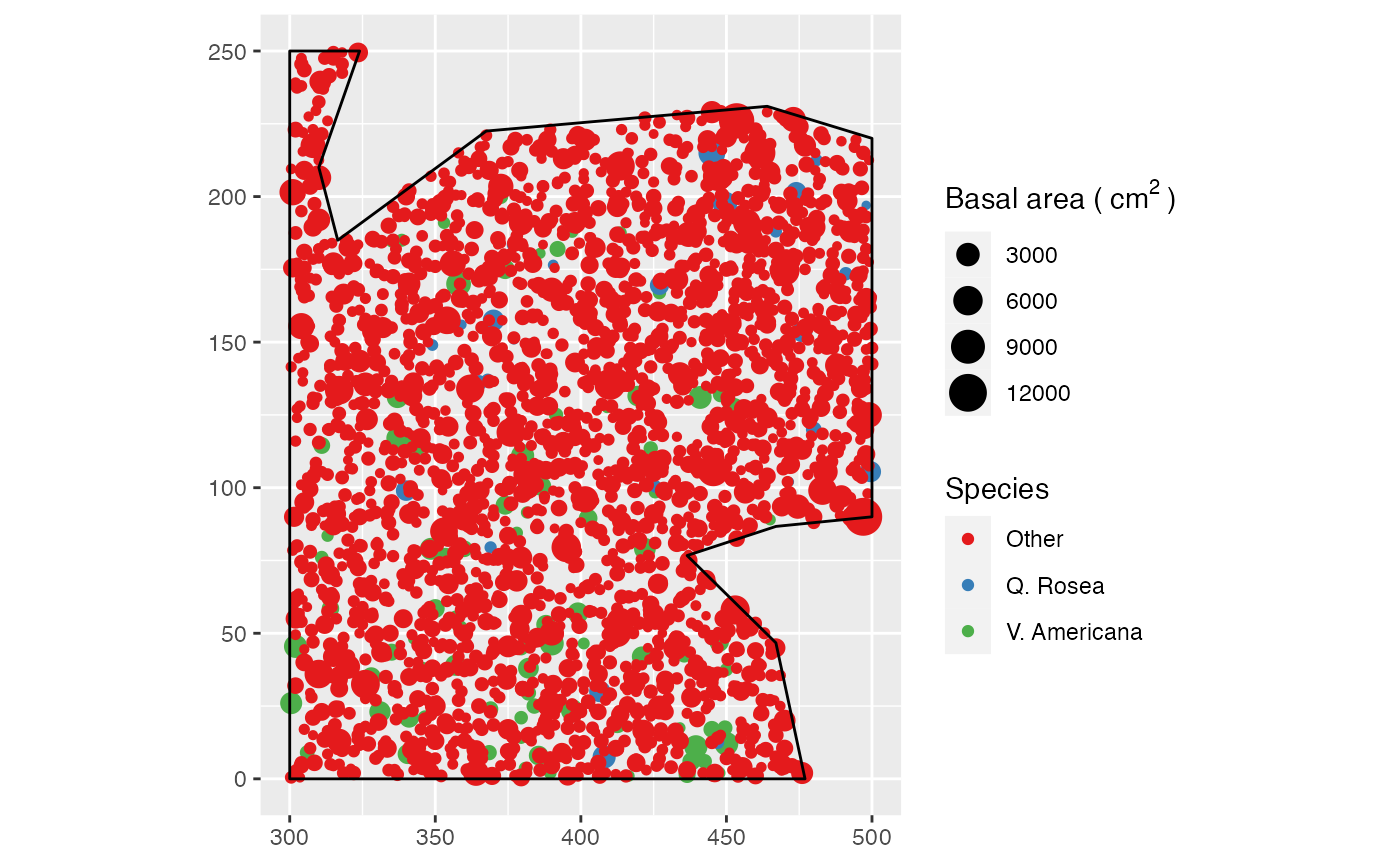
An example dataset is provided: it is a point pattern from the Paracou forest in French Guiana. Two species of trees are identified, other trees are of type “Other”. Point weights are their basal area, in square centimeters.

# Plot (second column of marks is Point Types) 
autoplot(
  paracou16, 
  labelSize = expression("Basal area (" ~cm^2~ ")"), 
  labelColor = "Species"
)

Main functions

The main functions of the package are designed to calculate distance-based measures of spatial structure. Those are non-parametric statistics able to summarize and test the spatial distribution (concentration, dispersion) of points.

The classical, topographic functions such as Ripley’s K are provided by the spatstat package and supported by dbmss for convenience.

Relative functions are available in dbmss only. These are the MM and mm and KdK_d functions.

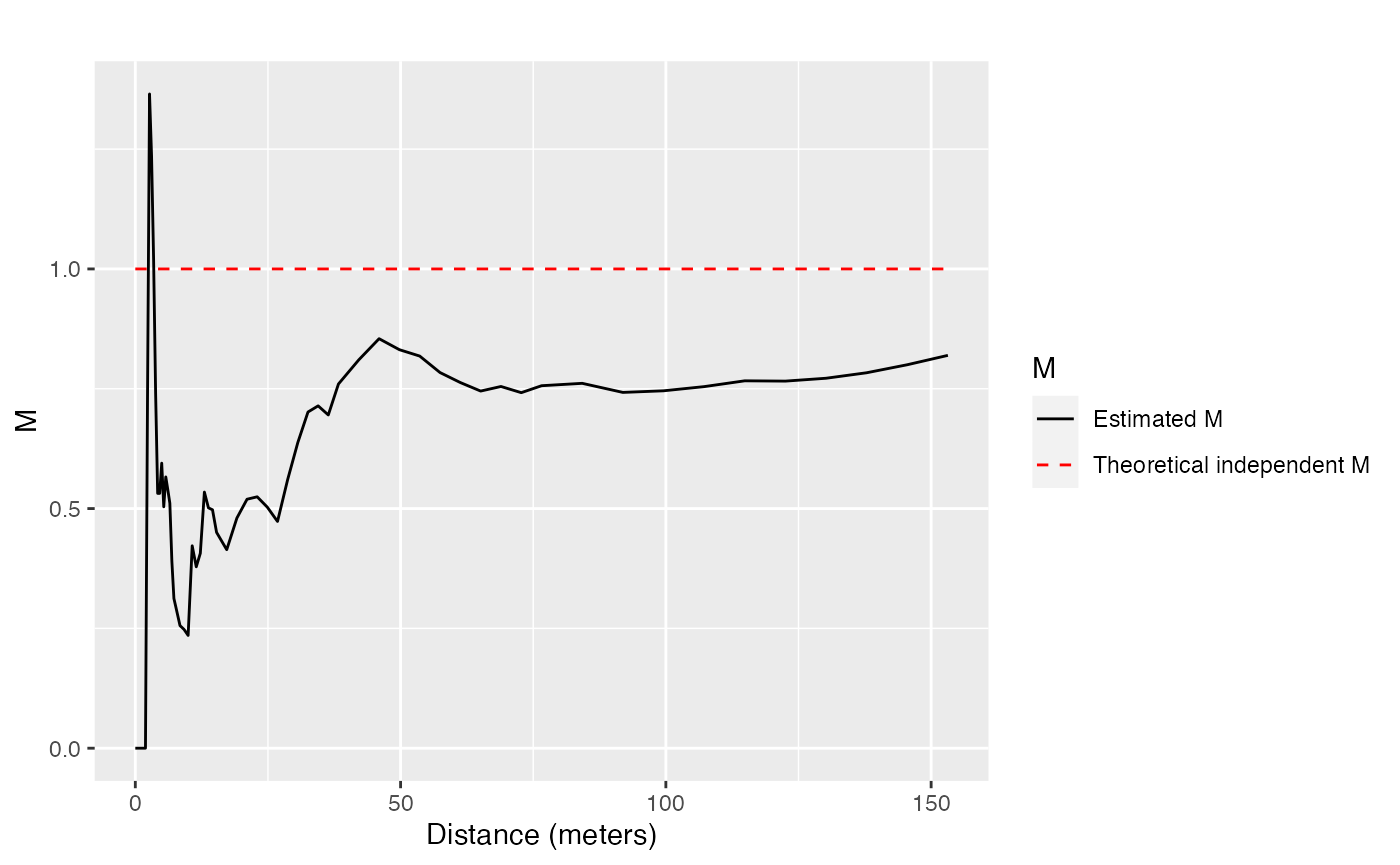
The bivariate MM function can be calculated for Q. Rosea trees around V. Americana trees:

autoplot(
  Mhat(
    paracou16, 
    ReferenceType = "V. Americana", 
    NeighborType = "Q. Rosea"
  ), 
  main = ""
)

Confidence envelopes

Confidence envelopes of various null hypotheses can be calculated. The univariate distribution of Q. Rosea is tested against the null hypothesis of random location.

autoplot(
  KdEnvelope(paracou16, ReferenceType = "Q. Rosea", Global = TRUE), 
  main = ""
)

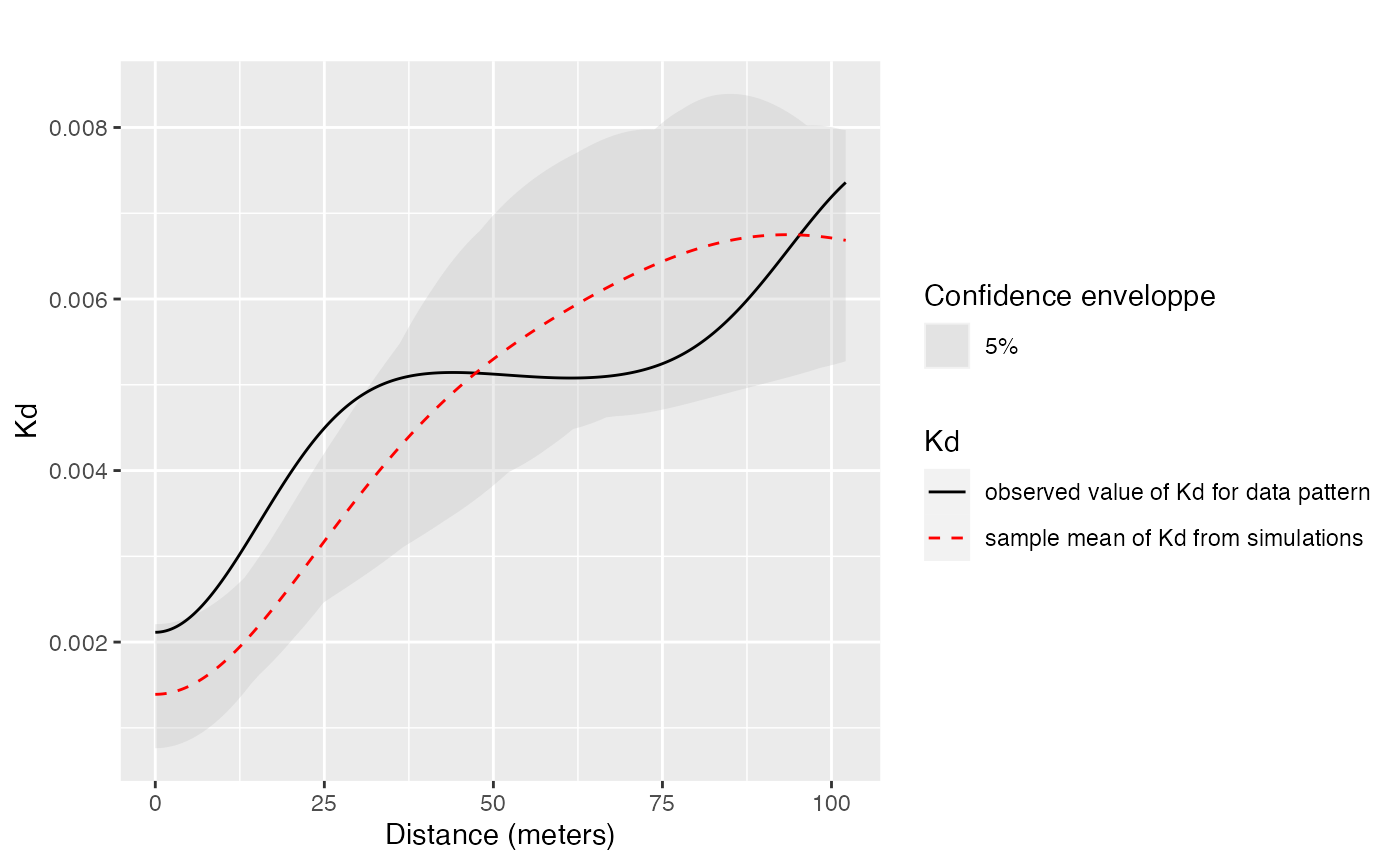
Significant concentration is detected between about 10 and 20 meters.

Maps

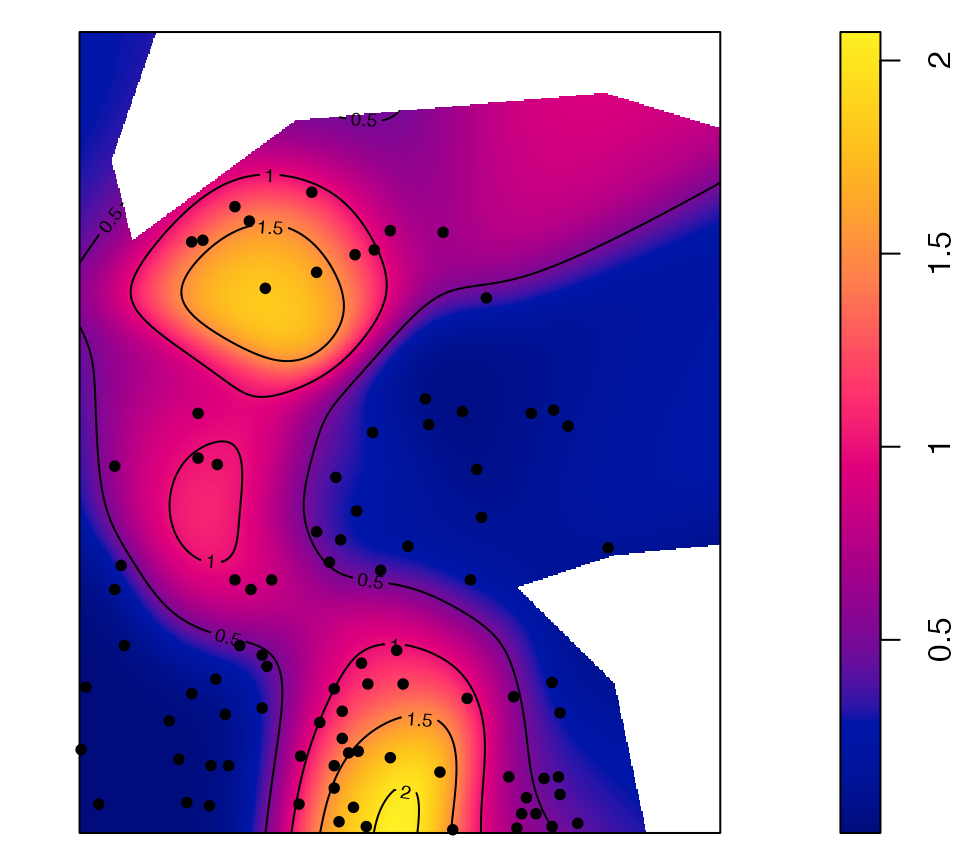
Individual values of some distance-based measures can be computed and mapped.

# Calculate individual intertype M(distance) value
ReferenceType <- "V. Americana"
NeighborType <- "Q. Rosea"
fvind <- Mhat(
  paracou16, 
  r = c(0, 30), 
  ReferenceType = ReferenceType, 
  NeighborType = NeighborType, 
  Individual = TRUE
)
# Plot the point pattern with values of M(30 meters)
p16_map <- Smooth(
  paracou16, 
  fvind = fvind, 
  distance = 30,
  # Resolution
  Nbx = 512, 
  Nby = 512
)
par(mar = rep(0, 4))
plot(p16_map, main = "")
# Add the reference points to the plot
is.ReferenceType <- marks(paracou16)$PointType == ReferenceType
points(
  x = paracou16$x[is.ReferenceType], 
  y = paracou16$y[is.ReferenceType], 
  pch = 20
)
# Add contour lines
contour(p16_map, nlevels = 5, add = TRUE)

Full documentation

https://ericmarcon.github.io/dbmss/