Goodness of Fit test between a distance based measure of spatial structure and simulations of its null hypothesis

Calculates the risk to reject the null hypothesis erroneously, based on the distribution of the simulations.

Usage

GoFtest(Envelope)

Arguments

Envelope: An envelope object (envelope) containing simulations in its simfuns attribute. It may be the result of any estimation function of the dbmss package or obtained by the envelope function with argument savefuns=TRUE.

Details

This test was introduced by Diggle(1983) and extensively developped by Loosmore and Ford (2006) for K, and applied to M by Marcon et al. (2012).

Value

A p-value.

References

Diggle, P. J. (1983). Statistical analysis of spatial point patterns. Academic Press, London. 148 p.

Loosmore, N. B. and Ford, E. D. (2006). Statistical inference using the G or K point pattern spatial statistics. Ecology 87(8): 1925-1931.

Marcon, E., F. Puech and S. Traissac (2012). Characterizing the relative spatial structure of point patterns. International Journal of Ecology 2012(Article ID 619281): 11.

Note

No support exists in the literature to apply the GoF test to non-cumulative functions (g, Kd...).

Ktest is a much better test (it does not rely on simulations) but it is limited to the K function against complete spatial randomness (CSR) in a rectangle window.

Examples

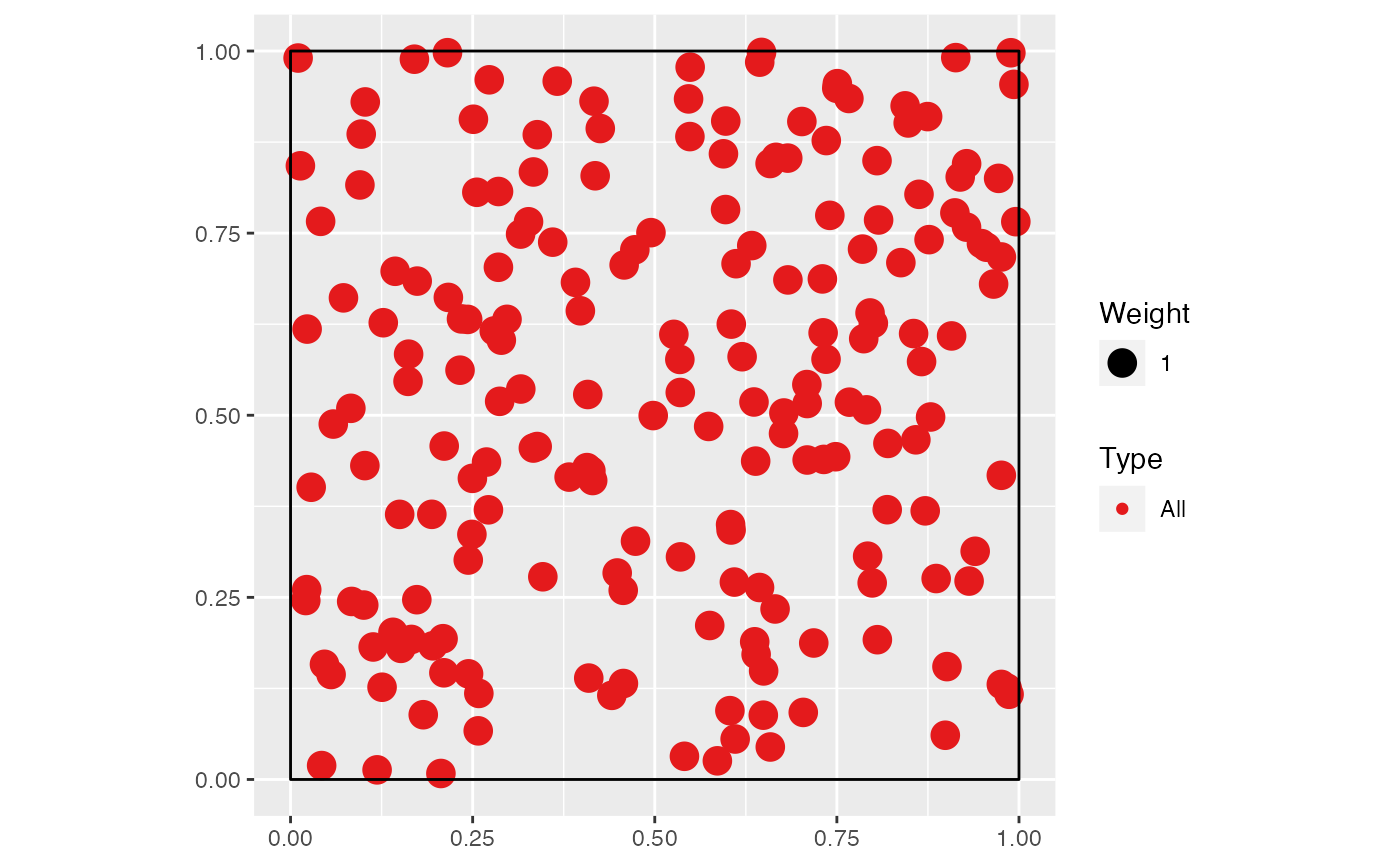
# Simulate a Matern (Neyman Scott) point pattern
nclust <- function(x0, y0, radius, n) {
  return(runifdisc(n, radius, centre=c(x0, y0)))
}
X <- rNeymanScott(20, 0.2, nclust, radius=0.3, n=10)
autoplot(as.wmppp(X))


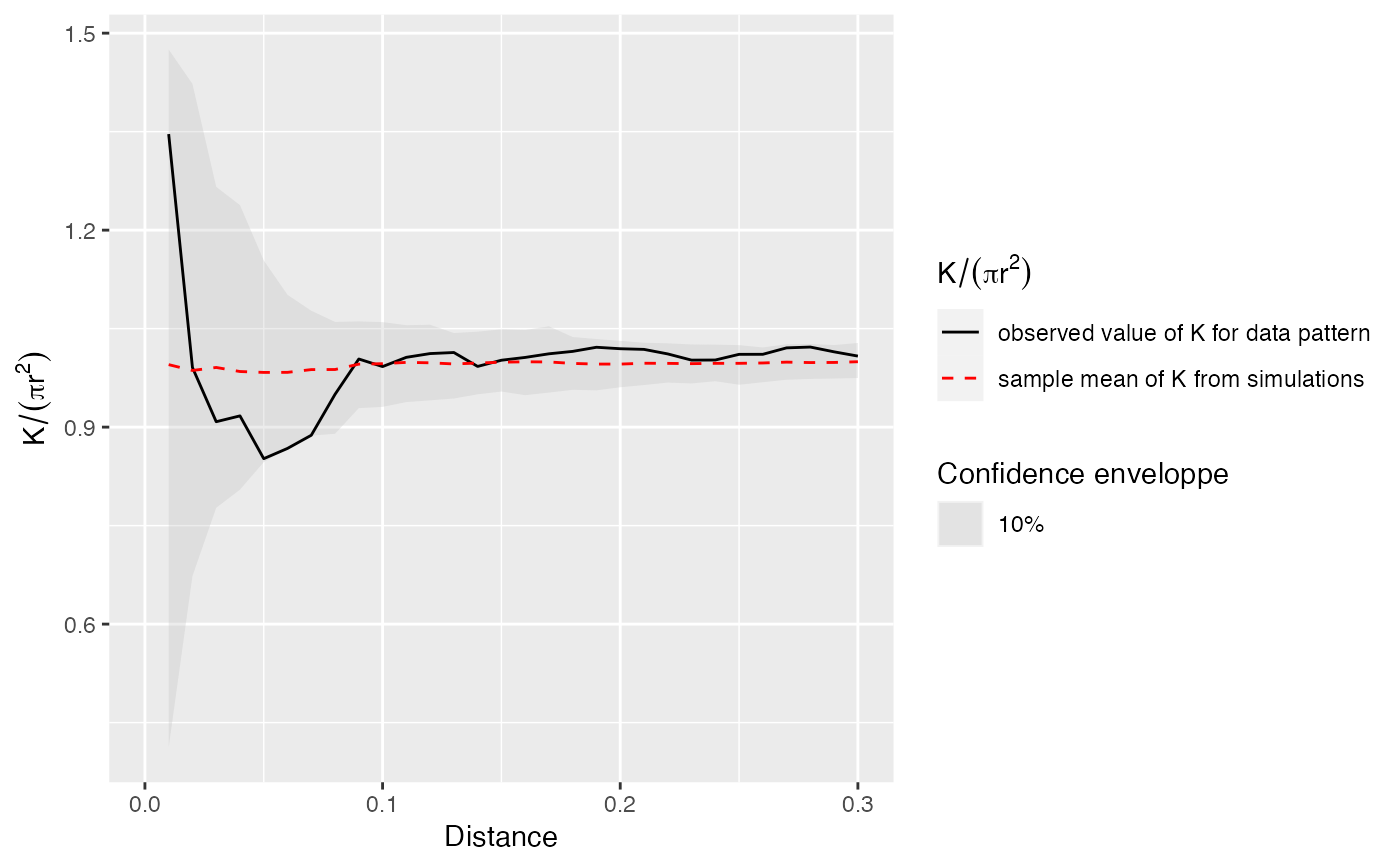
# Calculate confidence envelope (should be 1000 simulations, reduced to 50 to save time)
r <- seq(0, 0.3, 0.01)
NumberOfSimulations <- 50
Alpha <- .10
Envelope <- KEnvelope(as.wmppp(X), r, NumberOfSimulations, Alpha)
autoplot(Envelope, ./(pi*r^2) ~ r)


# GoF test. Power is correct if enough simulations are run (say >1000).
paste("p-value =", GoFtest(Envelope))
#> [1] "p-value = 0.86"