Skip to contents

Estimation of the m function

m_hat.Rd

Estimates the m function

Usage

mhat(X, r = NULL, ReferenceType, NeighborType = ReferenceType,
    CaseControl = FALSE, Original = TRUE, Approximate = ifelse(X$n < 10000, 0, 1),
    Adjust = 1, MaxRange = "ThirdW", Individual = FALSE, CheckArguments = TRUE)

Arguments

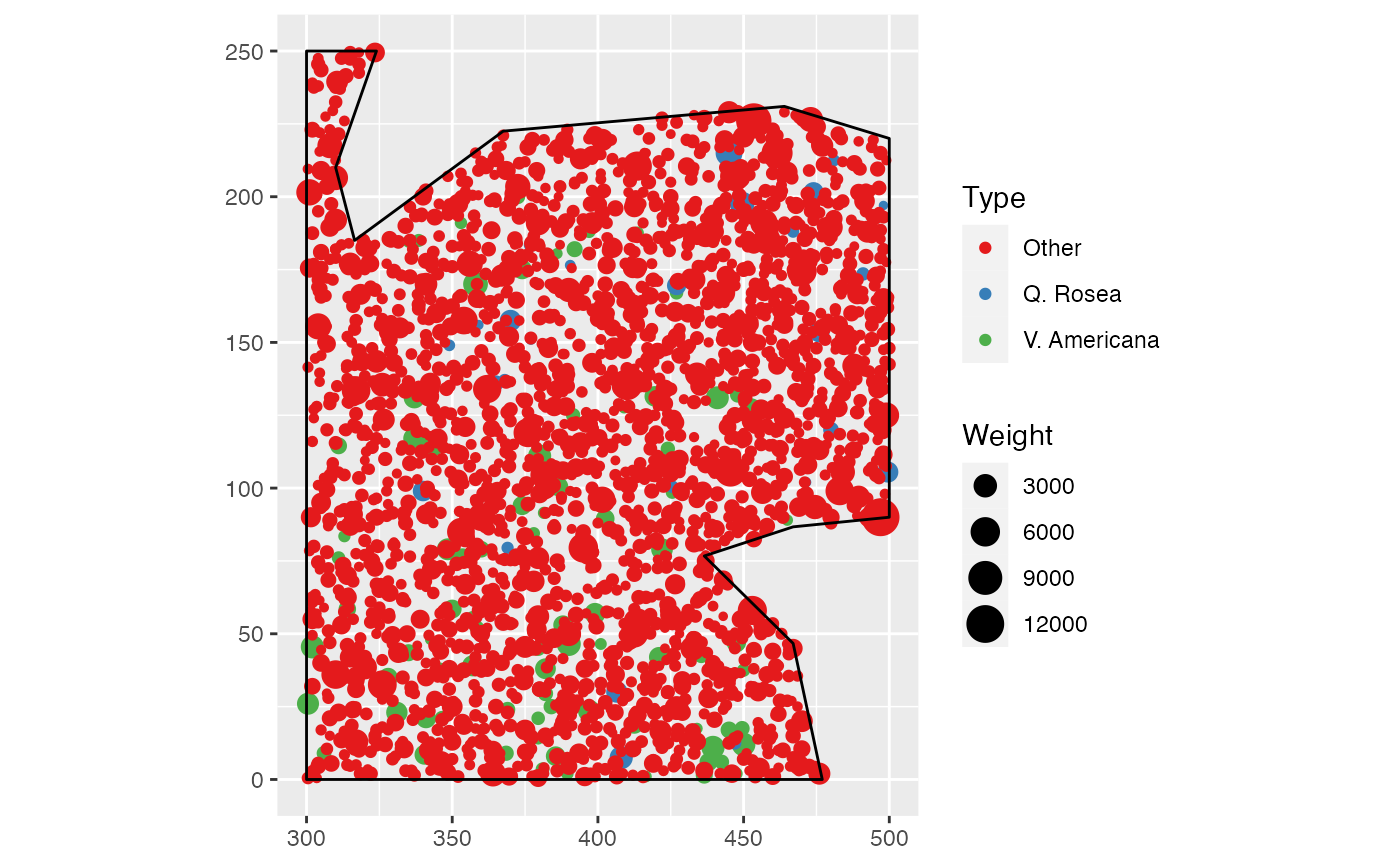
X

A weighted, marked planar point pattern (wmppp.object) or a Dtable object.

r

A vector of distances. If NULL, a default value is set: 512 equally spaced values are used, from the smallest distance to the range defined by MaxRange. the between points to half the diameter of the window.

ReferenceType

One of the point types.

NeighborType

One of the point types. By default, the same as reference type.

CaseControl

Logical; if TRUE, the case-control version of M is computed. ReferenceType points are cases, NeighborType points are controls.

Original

Logical; if TRUE (by default), the original bandwidth selection by Duranton and Overman (2005) following Silverman (1986: eq 3.31) is used. If FALSE, it is calculated following Sheather and Jones (1991), i.e. the state of the art. See bw.SJ for more details.

Approximate

if not 0 (1 is a good choice), exact distances between pairs of points are rounded to 1024 times Approximate single values equally spaced between 0 and the largest distance. This technique (Scholl and Brenner, 2015) allows saving a lot of memory when addressing large point sets (the default value is 1 over 10000 points). Increasing Approximate allows better precision at the cost of proportional memory use. Ignored if X is a Dtable object.

Adjust

Force the automatically selected bandwidth (following Original) to be multiplied by Adjust. Setting it to values lower than one (1/2 for example) will sharpen the estimation.

MaxRange

The maximum value of r to consider, ignored if r is not NULL. Default is "ThirdW", one third of the diameter of the window. Other choices are "HalfW", and "QuarterW" and "D02005". "HalfW", and "QuarterW" are for half or the quarter of the diameter of the window. "D02005" is for the median distance observed between points, following Duranton and Overman (2005). "ThirdW" should be close to "DO2005" but has the advantage to be independent of the point types chosen as ReferenceType and NeighborType, to simplify comparisons between different types. "D02005" is approximated by "ThirdW" if Approximate is not 0. If X is a Dtable object, the diameter of the window is taken as the max distance between points.

Individual

Logical; if TRUE, values of the function around each individual point are returned.

CheckArguments

Logical; if TRUE, the function arguments are verified. Should be set to FALSE to save time in simulations for example, when the arguments have been checked elsewhere.

Details

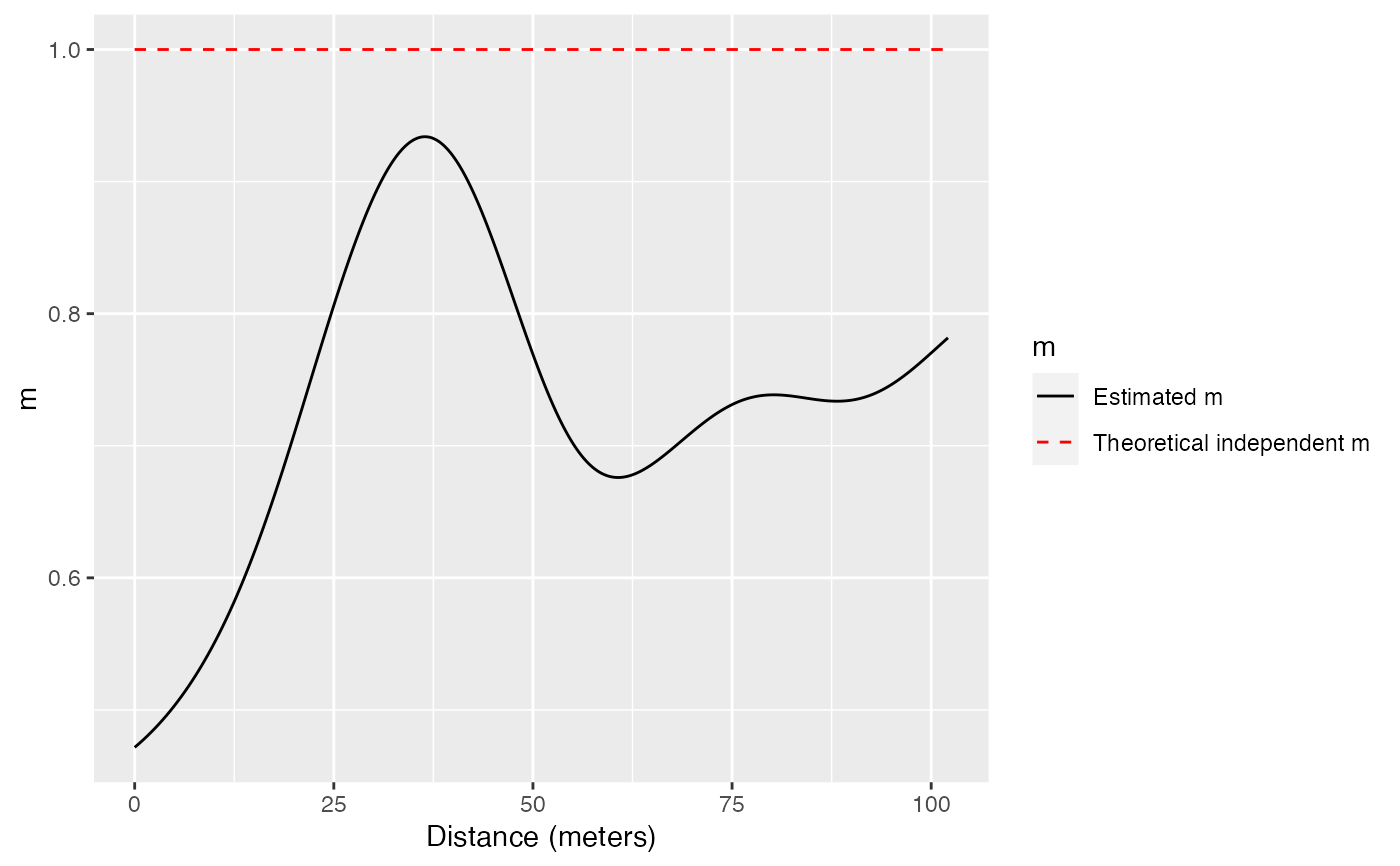
m is a weighted, density, relative measure of a point pattern structure (Lang et al., 2014). Its value at any distance is the ratio of neighbors of the NeighborType to all points around ReferenceType points, normalized by its value over the windows.

The number of neighbors at each distance is estimated by a Gaussian kernel whose bandwith is chosen optimally according to Silverman (1986: eq 3.31). It can be sharpened or smoothed by multiplying it by Adjust. The bandwidth of Sheather and Jones (1991) would be better but it is very slow to calculate for large point patterns and it sometimes fails. It is often sharper than that of Silverman.

If X is not a Dtable object, the maximum value of r is obtained from the geometry of the window rather than caculating the median distance between points as suggested by Duranton and Overman (2005) to save (a lot of) calculation time.

If CaseControl is TRUE, then ReferenceType points are cases and NeighborType points are controls. The univariate concentration of cases is calculated as if NeighborType was equal to ReferenceType, but only controls are considered when counting all points around cases (Marcon et al., 2012). This makes sense when the sampling design is such that all points of ReferenceType (the cases) but only a sample of the other points (the controls) are recorded. Then, the whole distribution of points is better represented by the controls alone.

Value

An object of class fv, see fv.object, which can be plotted directly using plot.fv.

If Individual is set to TRUE, the object also contains the value of the function around each individual ReferenceType point taken as the only reference point. The column names of the fv are "m_" followed by the point names, i.e. the row names of the marks of the point pattern.

Note

Estimating m relies on calculating distances, exactly or approximately (if Approximate is not 0). Then distances are smoothed by estimating their probability density. In contrast with Kdhat, reflection is not used to estimate density close to the lowest distance. The same kernel estimation is applied to the distances from reference points of neighbor points and of all points. Since m is a relative function, a ratio of densities is calculated, that makes the features of the estimation vanish.

Density estimation heavily relies on the bandwith. Starting from version 2.7, the optimal bandwith is computed from the distribution of distances between pairs of points up to twice the maximum distance considered. The consequence is that choosing a smaller range of distances in argument r results in less smoothed \(m\) values. The default values (r = NULL, MaxRange = "ThirdW") are such that almost all the pairs of points (except those more than 2/3 of the window diameter apart) are taken into account to determine the bandwith.

References

Duranton, G. and Overman, H. G. (2005). Testing for Localisation Using Micro-Geographic Data. Review of Economic Studies 72(4): 1077-1106.

Lang G., Marcon E. and Puech F. (2014) Distance-Based Measures of Spatial Concentration: Introducing a Relative Density Function. HAL 01082178, 1-18.

Marcon, E., F. Puech and S. Traissac (2012). Characterizing the relative spatial structure of point patterns. International Journal of Ecology 2012(Article ID 619281): 11.

Scholl, T. and Brenner, T. (2015) Optimizing distance-based methods for large data sets, Journal of Geographical Systems 17(4): 333-351.

Sheather, S. J. and Jones, M. C. (1991) A reliable data-based bandwidth selection method for kernel density estimation. Journal of the Royal Statistical Society series B, 53, 683-690.

Silverman, B. W. (1986). Density estimation for statistics and data analysis. Chapman and Hall, London.

See also

mEnvelope, Kdhat

Examples

data(paracou16)
autoplot(paracou16)


# Calculate M
autoplot(mhat(paracou16, , "V. Americana", "Q. Rosea"))