Estimation of the confidence envelope of the Kinhom function under its null hypothesis

Simulates point patterns according to the null hypothesis and returns the envelope of Kinhom according to the confidence level.

Usage

KinhomEnvelope(X, r = NULL, NumberOfSimulations = 100, Alpha = 0.05, 
               ReferenceType = "", lambda = NULL, SimulationType = "RandomPosition", 
               Global = FALSE, verbose = interactive())

Arguments

X: A point pattern (wmppp.object).
r: A vector of distances. If NULL, a sensible default value is chosen (512 intervals, from 0 to half the diameter of the window) following spatstat.
NumberOfSimulations: The number of simulations to run.
Alpha: The risk level.
ReferenceType: One of the point types. Default is all point types.
lambda: An estimation of the point pattern density, obtained by the density.ppp function.
SimulationType: A string describing the null hypothesis to simulate. The null hypothesis, may be "RandomPosition": points are drawn in an inhomogenous Poisson process (intensity is either lambda or estimated from X); "RandomLocation": points are redistributed across actual locations; "RandomLabeling": randomizes point types, keeping locations unchanged; "PopulationIndependence": keeps reference points unchanged, redistributes others across actual locations.
Global: Logical; if TRUE, a global envelope sensu Duranton and Overman (2005) is calculated.
verbose: Logical; if TRUE, print progress reports during the simulations.

Details

The random location null hypothesis is that of Duranton and Overman (2005). It is appropriate to test the univariate Kinhom function of a single point type, redistributing it over all point locations. It allows fixing lambda along simulations so the warning message can be ignored.

The random labeling hypothesis is appropriate for the bivariate Kinhom function.

The population independence hypothesis is that of Marcon and Puech (2010).

This envelope is local by default, that is to say it is computed separately at each distance. See Loosmore and Ford (2006) for a discussion.

The global envelope is calculated by iteration: the simulations reaching one of the upper or lower values at any distance are eliminated at each step. The process is repeated until Alpha / Number of simulations simulations are dropped. The remaining upper and lower bounds at all distances constitute the global envelope. Interpolation is used if the exact ratio cannot be reached.

Value

An envelope object (envelope). There are methods for print and plot for this class.

The fv contains the observed value of the function, its average simulated value and the confidence envelope.

References

Duranton, G. and Overman, H. G. (2005). Testing for Localisation Using Micro-Geographic Data. Review of Economic Studies 72(4): 1077-1106.

Kenkel, N. C. (1988). Pattern of Self-Thinning in Jack Pine: Testing the Random Mortality Hypothesis. Ecology 69(4): 1017-1024.

Loosmore, N. B. and Ford, E. D. (2006). Statistical inference using the G or K point pattern spatial statistics. Ecology 87(8): 1925-1931.

Marcon, E. and Puech, F. (2010). Measures of the Geographic Concentration of Industries: Improving Distance-Based Methods. Journal of Economic Geography 10(5): 745-762.

Marcon, E. and F. Puech (2017). A typology of distance-based measures of spatial concentration. Regional Science and Urban Economics. 62:56-67.

Examples

data(paracou16)
# Keep only 20% of points to run this example
X <- as.wmppp(rthin(paracou16, 0.2))
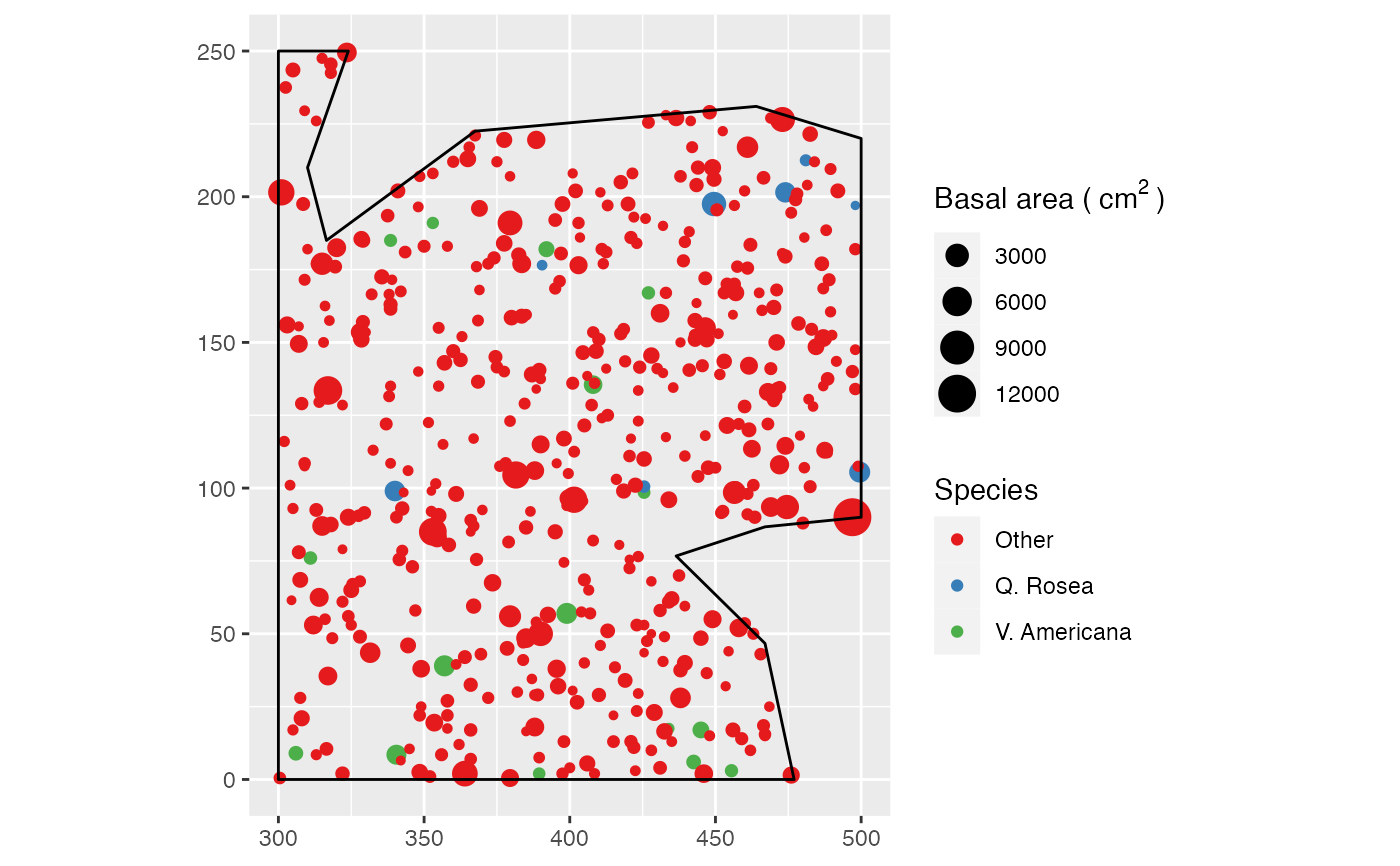
autoplot(X, 
  labelSize = expression("Basal area (" ~cm^2~ ")"), 
  labelColor = "Species")


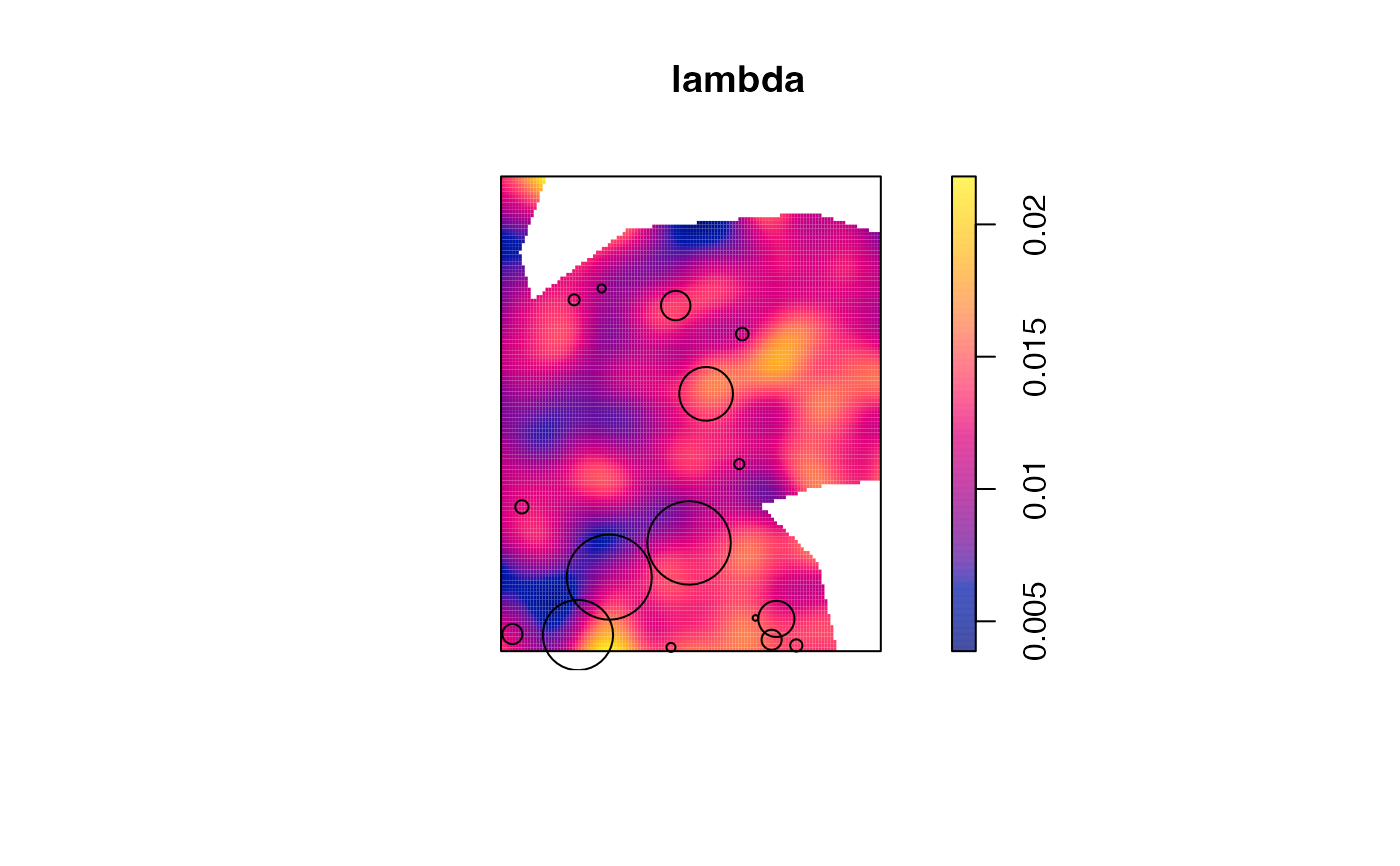
# Density of all trees
lambda <- density.ppp(X, bw.diggle(X))
plot(lambda)
V.americana <- X[X$marks$PointType=="V. Americana"]
plot(V.americana, add=TRUE)
#> Plotting the first column of marks


# Calculate Kinhom according to the density of all trees
# and confidence envelope (should be 1000 simulations, reduced to 4 to save time)
r <- 0:30
NumberOfSimulations <- 4
Alpha <- .10
autoplot(KinhomEnvelope(X, r,NumberOfSimulations, Alpha, , 
    SimulationType="RandomPosition", lambda=lambda), ./(pi*r^2) ~ r)