Introduction to SpatDiv

This is a preliminary version of a package designed to measure spatially-explicit diversity.

Getting started

Install the package for R from Github.

library("remotes")
remotes::install_github("EricMarcon/SpatDiv")

Demo

Create a random, spatialized community with 100 individuals of 10 species.

library("SpatDiv")
rSpCommunity(n = 1, size = 100, S = 3, Spatial = "Thomas") -> spCommunity
autoplot(spCommunity)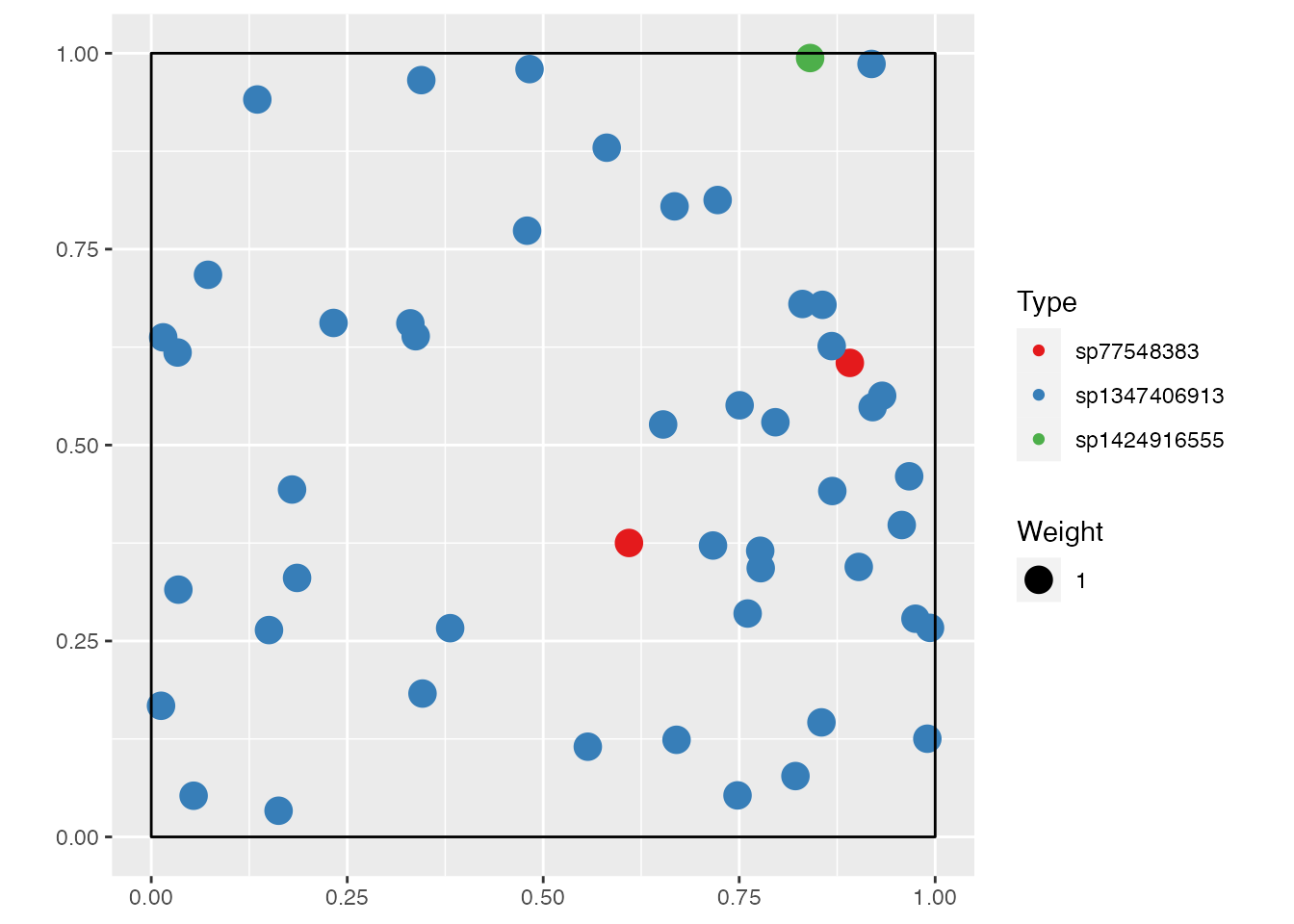

Plot a rank-abundance curve.

autoplot(as.AbdVector(spCommunity))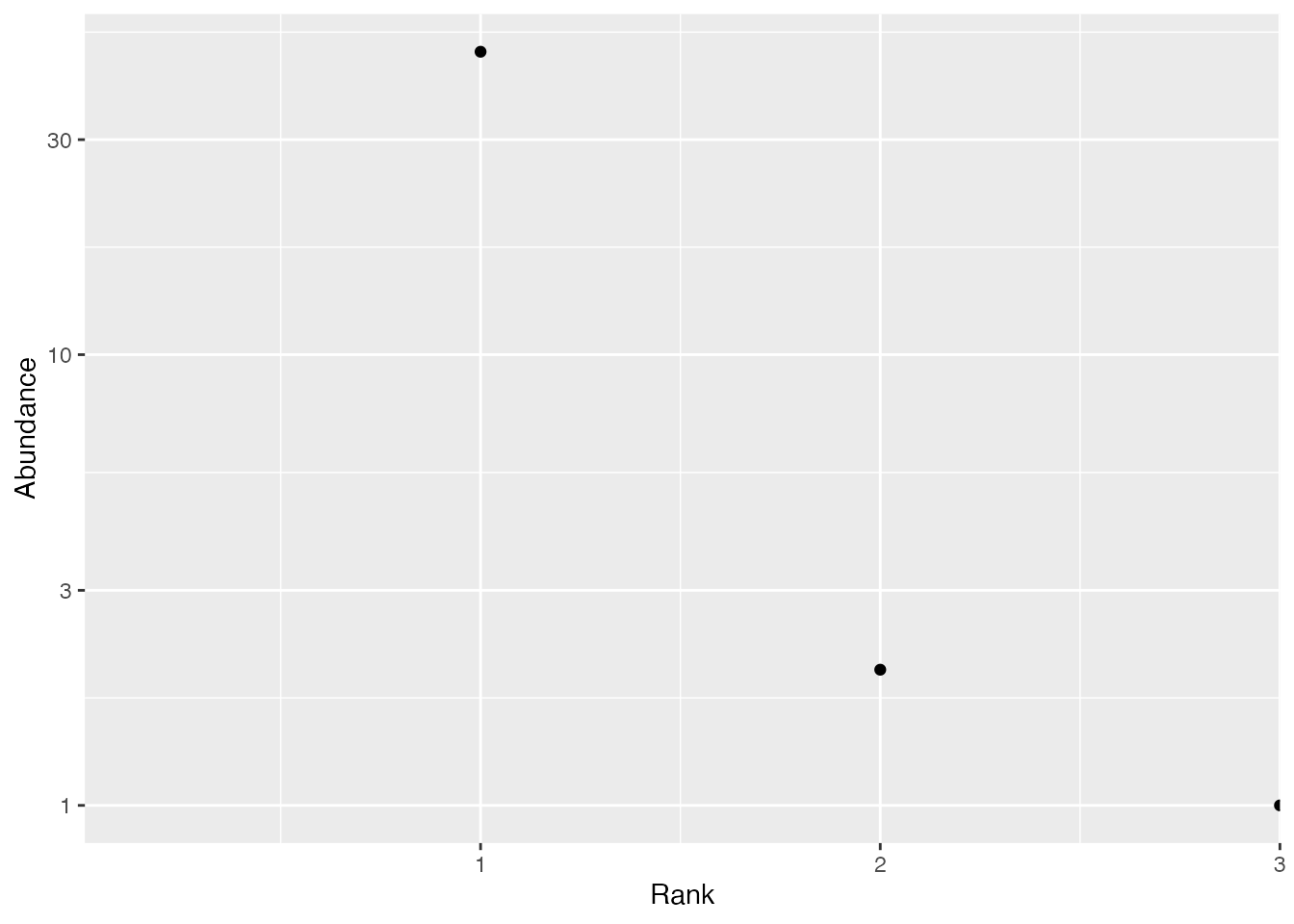

Diversity accumulation

With respect to the number of indiduals

Compute the Diversity Accumulation Curve for 1 to 50 neighbors for orders 0, 1 and 2, with the theoretical, null-model curve. Plot it for Shannon diversity.

divAccum <- DivAccum(spCommunity, n.seq = 1:50, q.seq = 0:2, H0 = "Multinomial",
    NumberOfSimulations = 1000)

autoplot(divAccum, q = 1)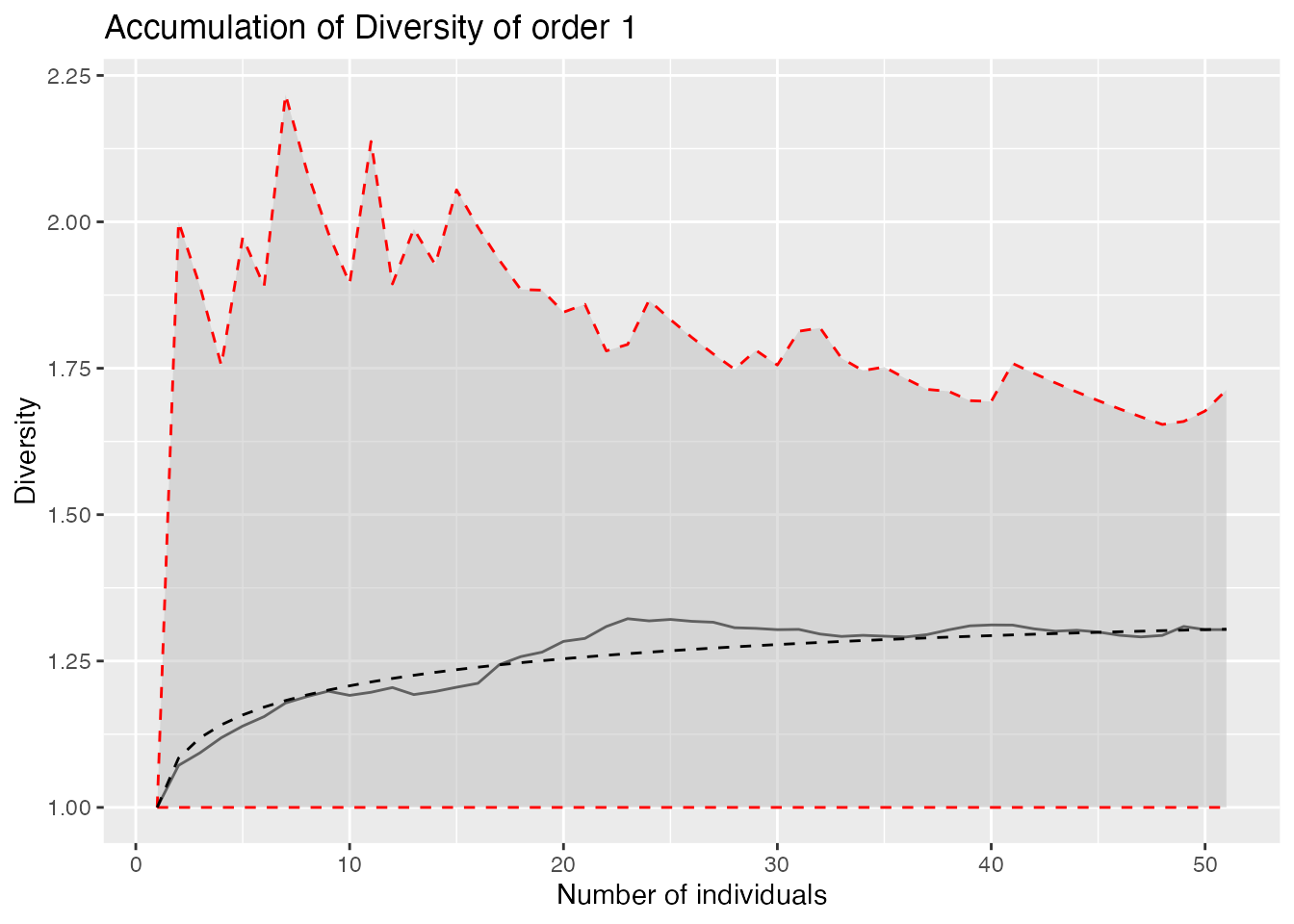

Compute and plot the mixing index of any order. Save the local values for future use.

mixing <- Mixing(spCommunity, n.seq = 1:50, q.seq = 0:2, H0 = "Multinomial", NumberOfSimulations = 1000,
    Individual = TRUE)

autoplot(mixing, q = 1)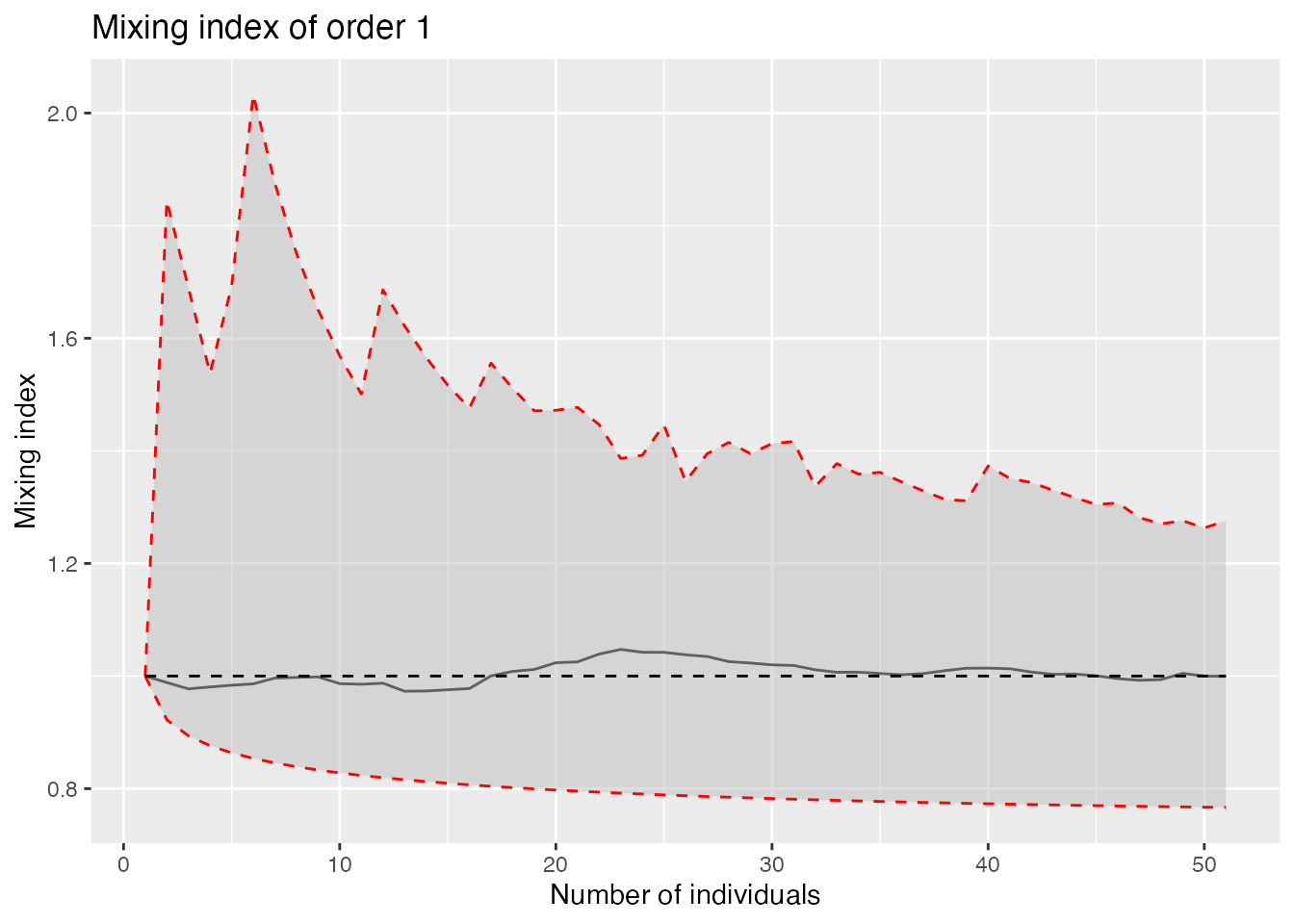

With respect to distance

The same accumulation curves can be computed by increasing the sample area around each point. The argument contains the vector of radii of those circular plots.

divAccum <- DivAccum(spCommunity, r.seq = seq(0, 0.5, by = 0.1), q.seq = 1, spCorrection = "Extrapolation",
    H0 = "Binomial")
autoplot(divAccum, q = 1)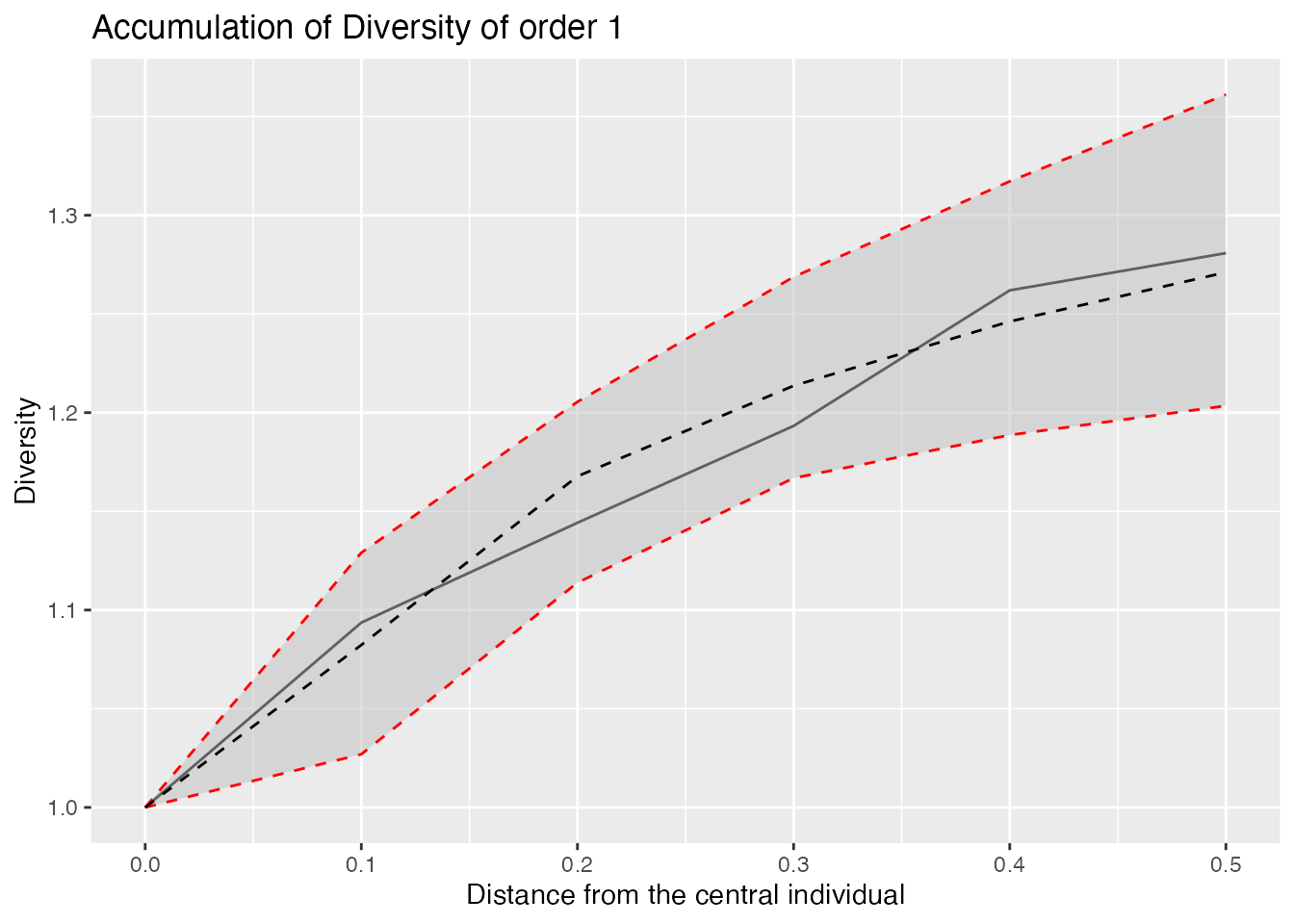

Null hypotheses

The actual accumulation curves of diversity and mixing index can be compared to null models with their confidence intervals. Values of the argument can be:

“None”: No null model is run.
“Multinomial”: The accumulation follows a multinomial sampling, with respect to the number of individuals only. The theoretical value and confidence envelope are calculated by the entropart package.
“Binomial”: The individuals are relocated in the window uniformly and independently.
“RandomLocation”: The individuals are relocated across their actual locations.

The multinomial null hypothesis is by far faster to compute than the others because it does not require point pattern simulations.

Map

Map the local diversity accumulation or mixing index, for example the species accumulation in 10 points (9 neighbors and the central point).

par(mar = c(0, 0, 0, 0))
MapPlot(mixing, Order = 0, NeighborHood = 10)

## [using ordinary kriging]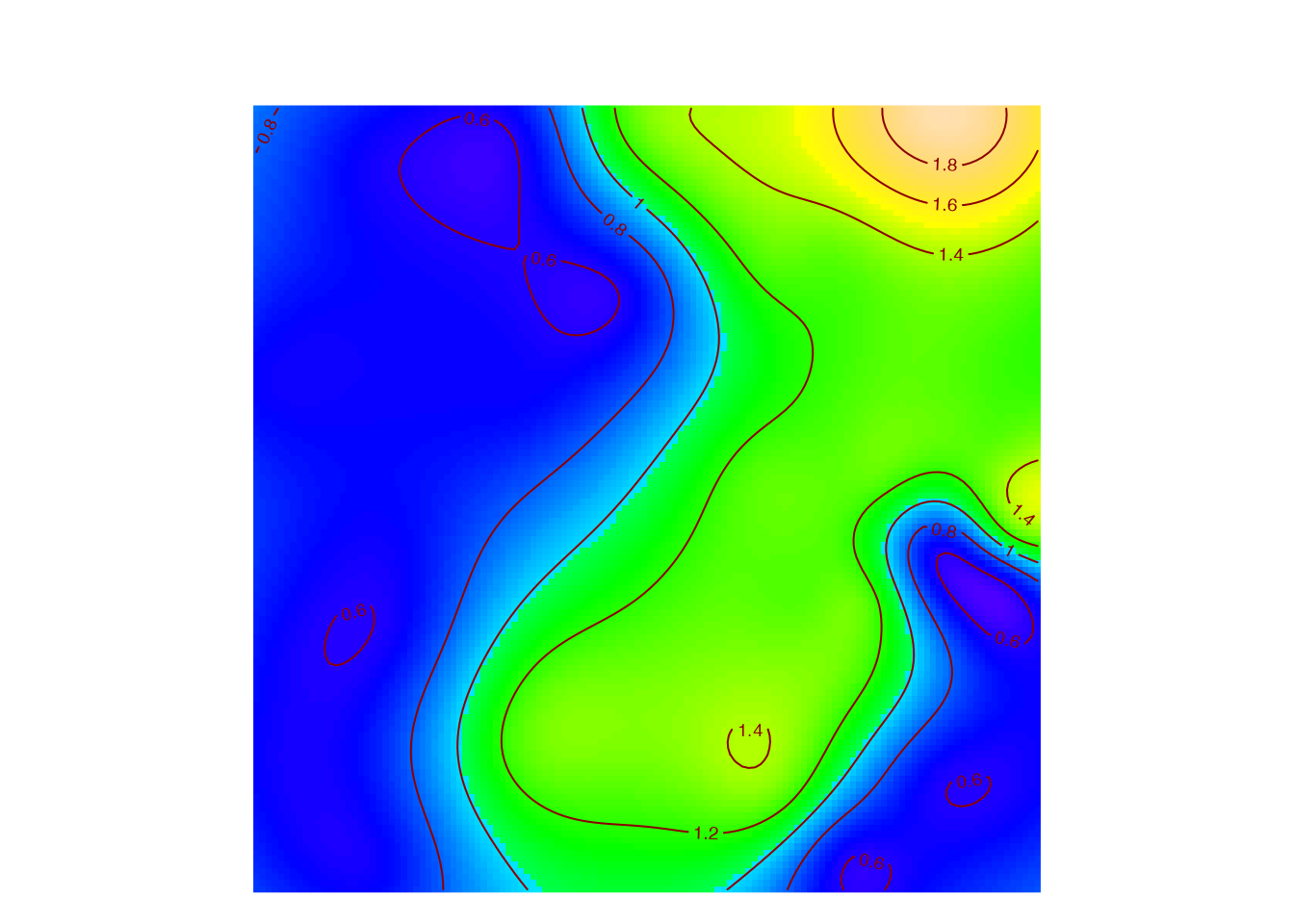

Spatially explicit diversity

Spatially explicit Simpson’s entropy

This is Simpson’s entropy in neighborhoods of points, closely related to Ripley’s K function. It is introduced as $(r)` by Shimatani (2001).

autoplot(Simpson_rEnvelope(spCommunity, Global = TRUE))

## Generating 100 simulations by evaluating expression  ...
## 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
## 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
## 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99,  100.
## 
## Done.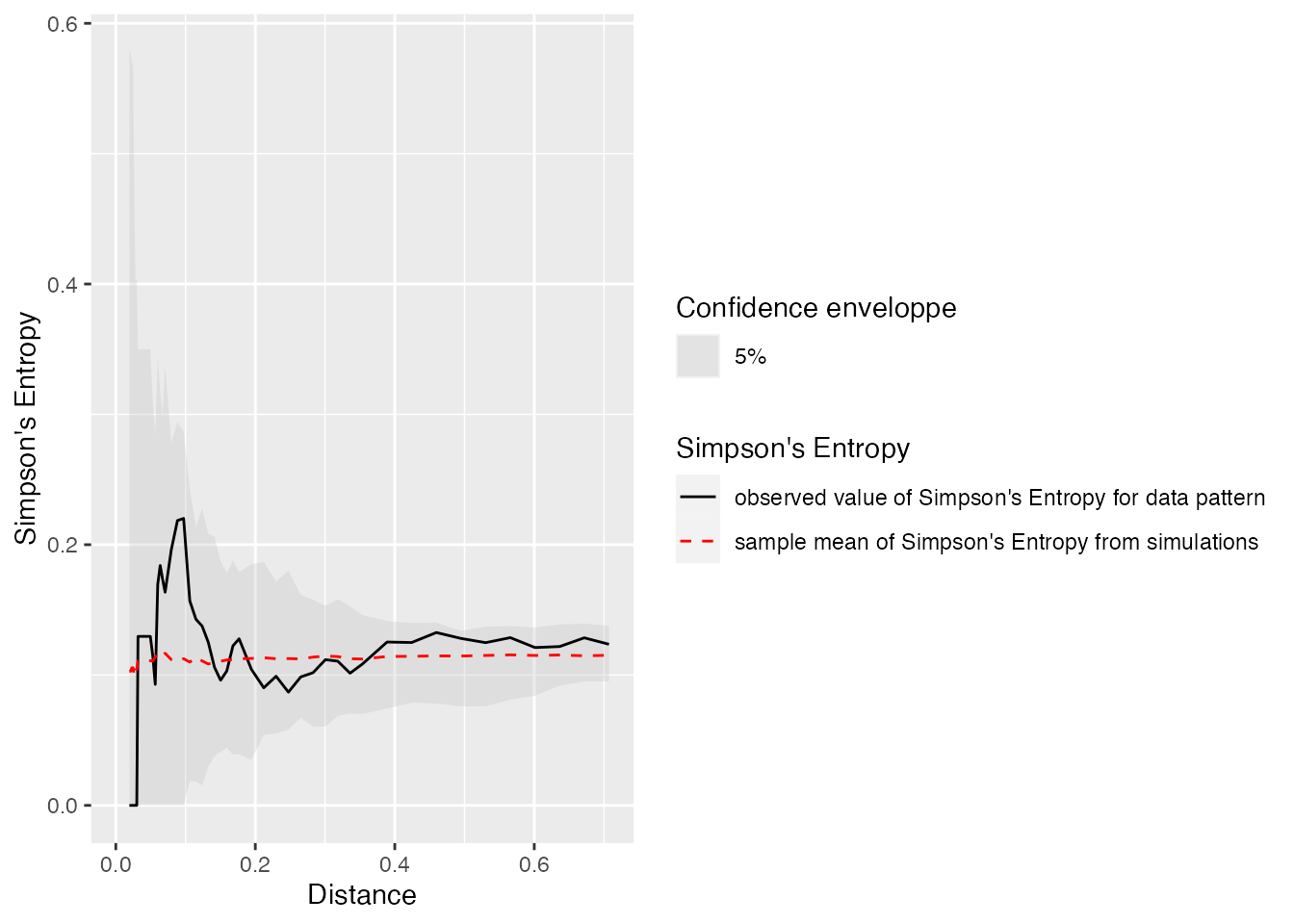

The Simpson_r() function computes the statistic. Simpson_rEnvelope() also computes the confidence interval of the null hypothesis, which is random labeling of the points by default.

References

Shimatani, Kenichiro. 2001. “Multivariate Point Processes and Spatial Variation of Species Diversity.” Forest Ecology and Management 142 (1-3): 215–29. https://doi.org/10.1016/s0378-1127(00)00352-2.

Spatially Explicit Measures of Diversity