2 Distribution de l’abondance des espèces (SAD)

La distribution de l’abondance des espèces (SAD : Species Abundance Distribution) est la loi statistique qui donne l’abondance attendue de chaque espèce d’une communauté. Les espèces ne sont pas identifiées individuellement, mais par le nombre d’individus leur appartenant.

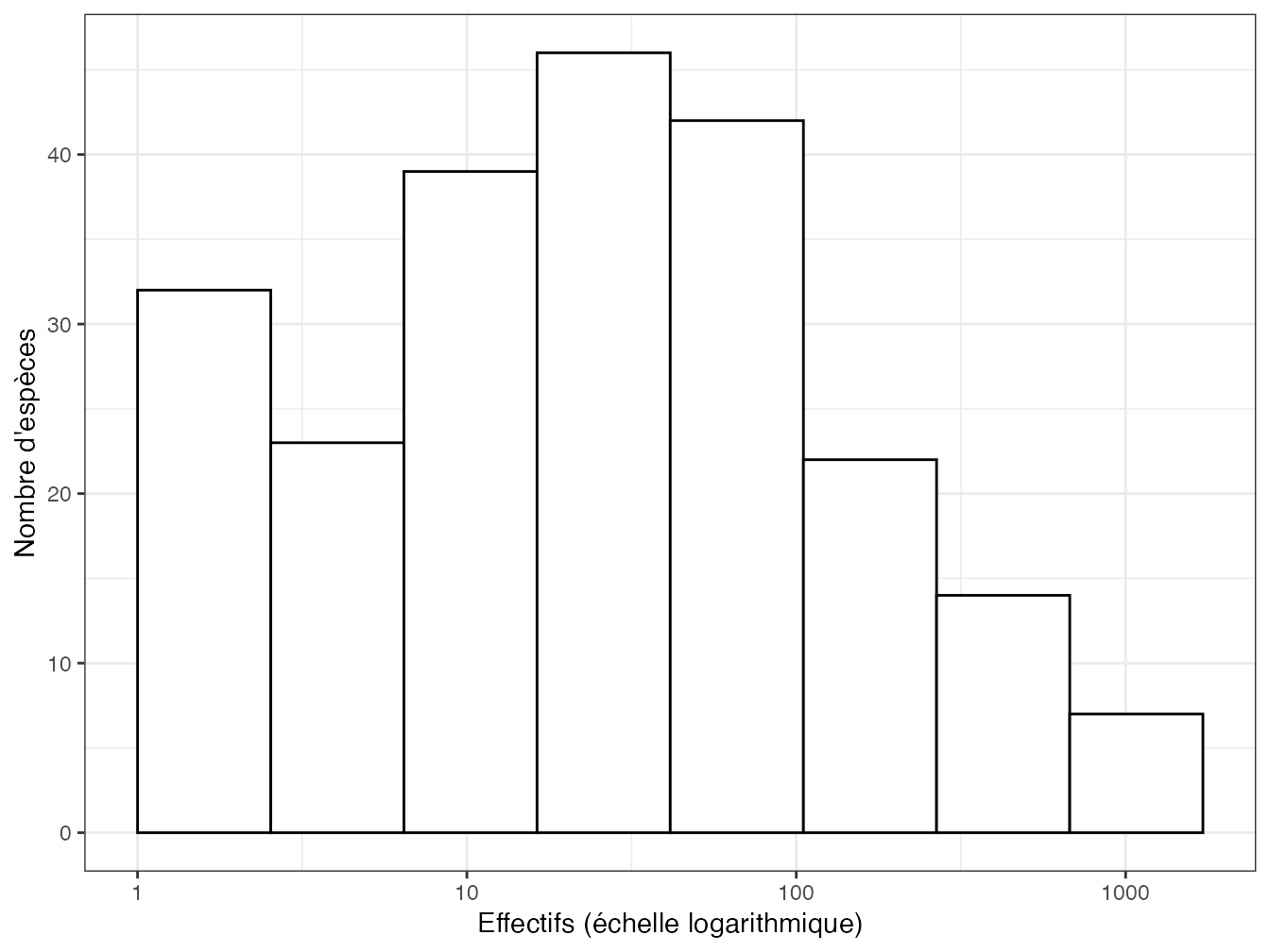
Histogramme des fréquences (diagramme de Preston) des arbres du dispositif de Barro Colorado Island. En abscisse : le nombre d’arbres de chaque espèce (en logarithme) ; en ordonnée : le nombre d’espèces.

Figure 2.1: Histogramme des fréquences (diagramme de Preston) des arbres du dispositif de Barro Colorado Island. En abscisse : le nombre d’arbres de chaque espèce (en logarithme) ; en ordonnée : le nombre d’espèces.

Elle peut être représentée sous la forme d’un histogramme des fréquences (diagramme de Preston (1948), figure 2.1) ou bien d’un diagramme rang-abondance (RAC : Rank Abundance Curve ou diagramme de Whittaker (1965), figure 2.2). Le RAC est souvent utilisé pour reconnaître des distributions connues. Izsák and Pavoine (2012) ont étudié les propriétés des RAC pour les principales SAD.

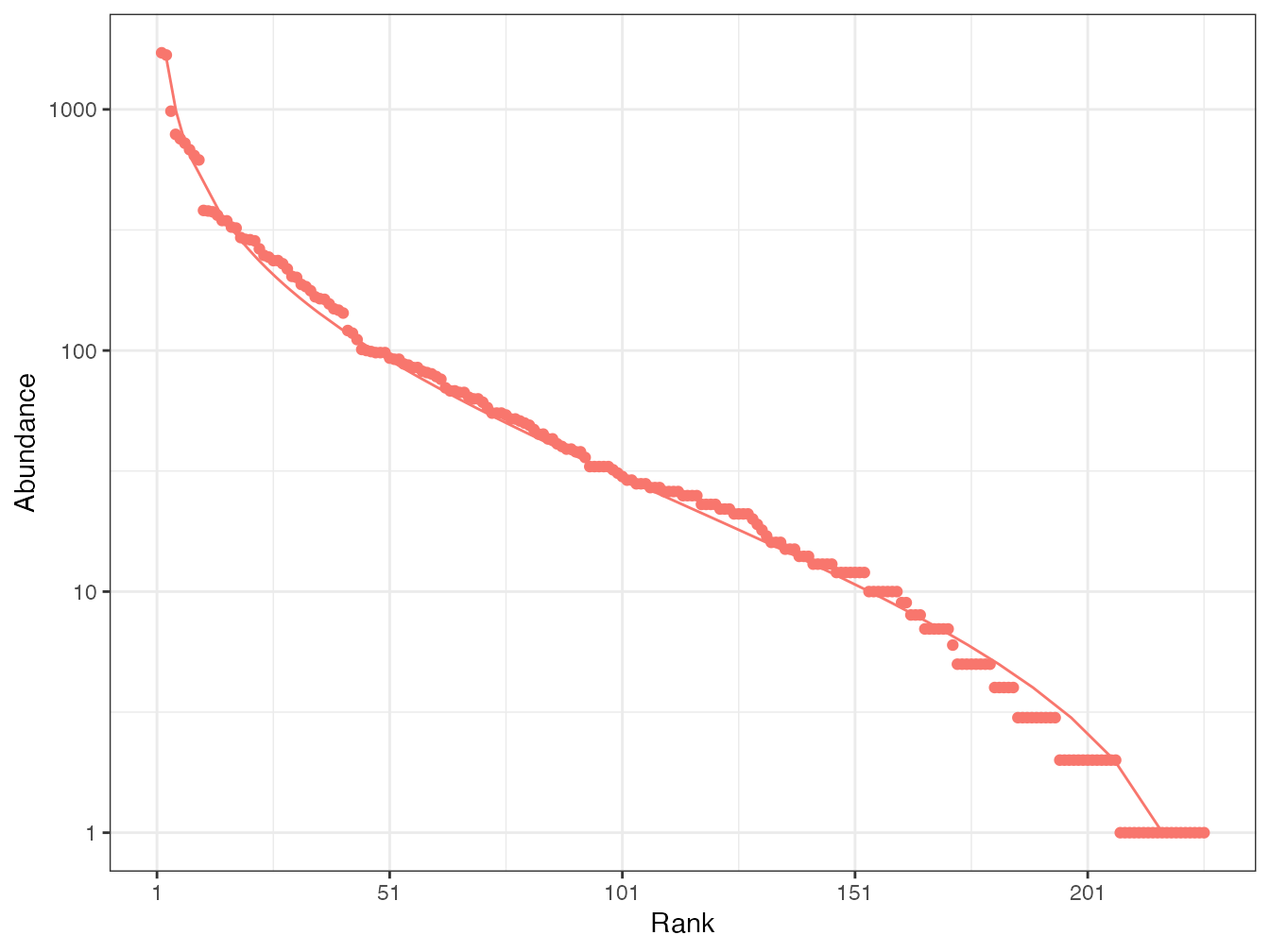
Diagramme rang-abondance (diagramme de Whittaker) des arbres du dispositif de Barro Colorado Island. Les points sont les données : en abscisse : le rang de l’espèce, à partir de la plus abondante ; en ordonnée : l’abondance de l’espèce. La courbe est l’ajustement d’une distribution log-normale.

Figure 2.2: Diagramme rang-abondance (diagramme de Whittaker) des arbres du dispositif de Barro Colorado Island. Les points sont les données : en abscisse : le rang de l’espèce, à partir de la plus abondante ; en ordonnée : l’abondance de l’espèce. La courbe est l’ajustement d’une distribution log-normale.

Code de la figure 2.1 :

BCI_abd <- sort(colSums(BCI), decreasing = TRUE)
ggplot(data.frame(BCI_abd), aes(BCI_abd)) + 
  geom_histogram(
    bins = nclass.Sturges(log(BCI_abd)), 
    color = "black", 
    fill = "white",
    boundary = 0
  ) +
  scale_x_log10() +
  labs(
    x = "Effectifs (échelle logarithmique)", 
    y = "Nombre d'espèces"
  )

Code de la figure 2.2 :

library("divent")
BCI_abd %>% 
  as_abundances() %>% 
  autoplot(fit_rac = TRUE, distribution = "lnorm")

Les SAD sont traitées en détail par Magurran (1988) ou McGill et al. (2007). Les principales distributions, nécessaires à la compréhension de la suite sont présentées ici :

La distribution en log-séries de Fisher, Corbet, and Williams (1943) ;
La distribution géométrique (Motomura 1932; Whittaker 1972) ;
La distribution log-normale (Preston 1948) ;
Le modèle Broken Stick (MacArthur 1957).

Formellement, la distribution des probabilités des espèces, notées $p_s$, est à établir.

2.1 La distribution en log-séries

Cette distribution est traitée en détail dans le chapitre ??.

Le nombre d’espèces est lié au nombre d’individus par la relation ${\mathbb E}(S^n) = \alpha \ln(1 + n / \alpha)$ où $S^n$ indique le nombre d’espèces observées dans un échantillon de $n$ individus. $\alpha$ est le paramètre qui fixe la pente de la partie linéaire de la relation, valide dès que $n \gg \alpha$, où le nombre d’espèces $S^n$ augmente proportionnellement au logarithme du nombre d’individus $\ln(n)$.

La distribution a été obtenue à partir d’inventaires de communautés de papillons en Malaisie et en Angleterre. Le modèle est tombé en désuétude faute de confirmation empirique à l’échelle de la communauté, avant d’être remis en valeur par la théorie neutre (Stephen P. Hubbell 2001) dans lequel la distribution de la méta-communauté est en log-séries.

2.2 La distribution Broken Stick

Si les espèces se partagent les ressources ou l’espace des niches, représentées par un bâton, par un processus de cassure aléatoire et simultanée (précisément, les $S-1$ cassures du bâton sont distribuées uniformément sur sa longueur) et que leur abondance est proportionnelle à la quantité de ressources ou d’espace de niche obtenus, alors leur distribution suit le modèle Broken Stick de MacArthur (1957).

Parmi les distributions classiques, c’est la plus équitable : la distribution uniforme des probabilités ($p_s = 1 / S$ pour tout $s$) n’est jamais approchée.

Elle est peu observée empiriquement.

2.3 La distribution log-normale

Dans une distribution log-normale, le logarithme des probabilités des espèces (notées $p_s$ pour l’espèce $s$) suit une loi normale. L’écart-type $\sigma$ de cette distribution règle l’équitabilité de la distribution. Son espérance est obtenue à partir du nombre d’espèces et de $\sigma$, pour que la somme des probabilités égale 1.

May (1975) explique cette distribution par le théorème de la limite centrale : la variable aléatoire valant 1 si un individu est de l’espèce $s$ et 0 sinon est le produit de nombreuses variables de loi inconnues valant 1 en cas de succès (germination d’une graine, survie à de nombreux évènements…). Le logarithme de ce produit est une somme de variables aléatoire dont la loi est forcément normale par application du théorème de la limite centrale.

La distribution est aussi le résultat d’un algorithme de bâton brisé (broken stick) hiérarchique (Bulmer 1974) :

Si les ressources (représentées par un bâton) sont partagées une première fois aléatoirement, selon une loi quelconque,
Si chaque bâton obtenu est partagé à nouveau selon le même procédé, et que l’opération est répétée un assez grand nombre de fois,
Si l’abondance de chaque espèce est proportionnelle aux ressources dont elle dispose,
Alors la distribution des espèces est log-normale.

Ce mécanisme décrit assez bien un mécanisme de partage successif des ressources, par exemple entre groupes d’espèces de plus en plus petits, correspondant à des niches écologiques de plus en plus étroites.

D’autres arguments existent dans la littérature. Par exemple, Engen and Lande (1996) obtiennent une distribution normale à partir d’un modèle de dynamique des populations.

La distribution log-normale décrit assez bien (mais pas exactement) une communauté locale dans le cadre de la théorie neutre (Stephen P. Hubbell 2001) comme le montre la figure 2.2. Le nombre d’espèces rares est un peu surestimé. La distribution exacte est donnée par Volkov et al. (2003).

2.4 La distribution géométrique

Si les espèces se partagent les ressources selon un algorithme broken stick séquentiel (comme dans la distribution log-normale) mais de proportion fixe $0<k<1$, alors la distribution obtenue est géométrique. Les abondances successives sont proportionnelles à $k, k(1-k), k(1-k)^2, \dots, k(1-k)^s, \dots, k(1-k)^S$.

Ce modèle a été établi par Motomura (1932) cité par May (1975). Ses propriétés ont été étudiées par Whittaker (1972).

C’est la distribution qui traduit l’absence de relation entre la taille de l’échantillon et l’abondance des espèces (Pueyo, He, and Zillio 2007) : la distribution du logarithme de ses probabilités est uniforme. En d’autre termes, l’ordre de grandeur de l’abondance d’une espèce est uniformément distribué.

La distribution est observée dans les communautés pionnières (Bazzaz1975?), peu diverses, ou les communautés microbiennes (Haegeman et al. 2013).

2.5 Synthèse

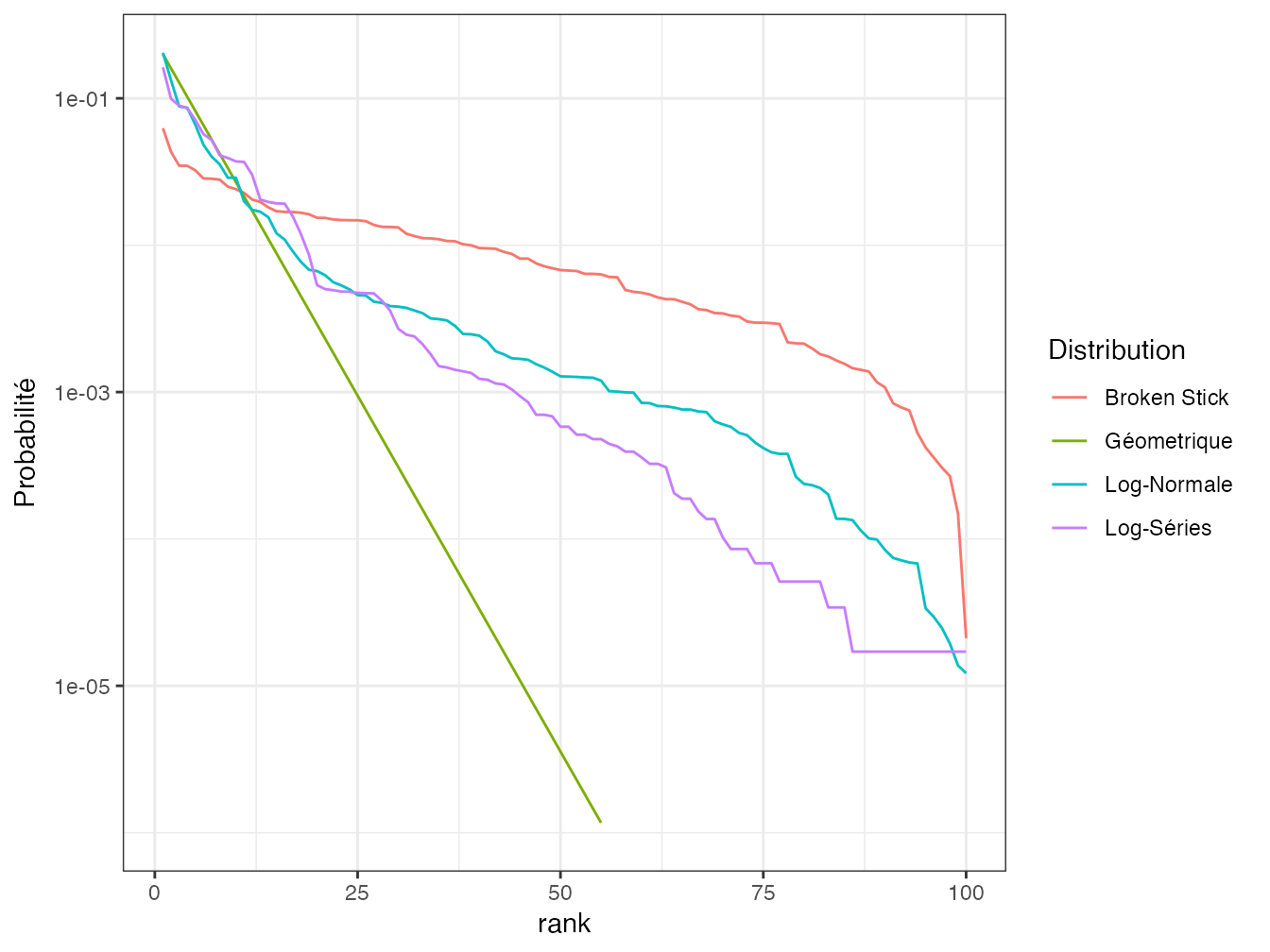
$Diagramme rang-fréquence des distributions de probabilité classiques. Toutes les distributions sont de 100 espèces. Les probabilités inférieures à $10^{-6}$ ne sont pas affichées. Les paramètres choisis sont $\alpha=11$ pour la distribution log-séries, $k=0,2$ pour la distribution géométrique et $\sigma=2$ pour la distribution log-normale.$

Figure 2.3: Diagramme rang-fréquence des distributions de probabilité classiques. Toutes les distributions sont de 100 espèces. Les probabilités inférieures à $10^{-6}$ ne sont pas affichées. Les paramètres choisis sont $\alpha=11$ pour la distribution log-séries, $k=0,2$ pour la distribution géométrique et $\sigma=2$ pour la distribution log-normale.

La figure 2.3 est inspirée de la figure très connue de Magurran (1988). Elle montre bien une gradation en termes de décroissance de probabilité entre des distributions de même richesse : de la plus équitable (broken stick) à la plus inéquitable (géométrique). Elle doit être nuancée : la proportion $k$ de la distribution géométrique fixe la pente de la droite qui la représente sur la figure. $k=10\%$ sur la figure : une valeur plus faible diminuerait la pente. De même, l’écart-type de la distribution log-normale décrit sa dispersion. Une valeur supérieure augmenterait sa décroissance.

Le code utilisé pour produire la figure 2.3 est le suivant :

library("divent")
# Tirage d'une communauté en log-séries
size <- 1E5
alpha <- 11
species_number <- -alpha * log(alpha / (size + alpha))
abd_lseries <- rlseries(species_number, size, alpha)
# Part des ressources accaparées dans la distribution géométrique
prob <- 0.2
# Calcul des probabilités de la distribution géométrique
prob_geom <- prob / (1 - (1 - prob)^species_number) * (1 - prob)^(0:(species_number - 1))
# Dispersion de la loi lognormale
sd <- 2
# Tirage de S valeurs dans une loi lognormale
abd_lnorm <- rlnorm(species_number, meanlog = 0, sdlog = sd)
# Tirage des probabilités de la distribution broken stick
prob_bstick <- c(cuts <- sort(stats::runif(species_number - 1)), 1) - c(0, cuts)
# Graphique
tibble(
  rank = 1:species_number,
  `Log-Séries` = sort(abd_lseries / sum(abd_lseries), decreasing = TRUE),
  `Géometrique` = sort(prob_geom, decreasing = TRUE),
  `Log-Normale` = sort(abd_lnorm / sum(abd_lnorm), decreasing = TRUE),
  `Broken Stick` = sort(prob_bstick, decreasing = TRUE)) %>% 
  pivot_longer(cols = -rank) %>% 
  ggplot() +
    geom_line(aes(x = rank, y = value, color = name)) +
    scale_y_log10(limits = c(1E-6, NA)) +
    labs(y = "Probabilité", color = "Distribution")

La simulation de ces quatre distributions peut être réalisée par la fonction rcommunity() du package divent, où l’argument distribution peut valoir “bstick”, “lnorm”, “geom” ou “lseries”. La simulation des communautés autres que log-séries passe par le tirage des probabilités des espèces (le calcul est déterministe dans le cas de la distribution géométrique) puis le tirage d’un nombre d’individus dans une loi multinomiale respectant ces probabilités et l’effectif total.

La fonction fit_rac() permet d’inférer les paramètres d’une distribution à partir d’un vecteur d’abondance. La distribution correspondant au modèle estimé peut être affichée sur la figure Rang-Abondance (figure 2.1).

Le package sads fournit les fonctions classiques de R (densité de probabilité, cumulative, quantile, simulation) pour les distributions utiles en écologie, au-delà de celles présentées ici. La distribution de Volkov notamment peut être simulée. Les fonctions fitxxx() complètent la fonction fit_rac() de divent. Enfin, la fonction radfit() du package vegan ajuste aux données en même temps les distributions broken-stick (désignée par “Null”), géométrique (“Preemption”) et lognormale, inclut les distributions de Zipf et de Mandelbrot non traitées ici, mais ignore les log-séries. Les vraisemblances des différents modèles sont comparées pour choisir celui qui s’ajuste le mieux.

Le code suivant montre comment ajuster une distribution log-normale aux données de BCI avec divent ou sads.

# divent
library("divent")
fit_divent_lnorm <- fit_rac(BCI_abd, distribution = "lnorm")
# Affichage des paramètres estimés
fit_divent_lnorm$parameters

## # A tibble: 1 × 2
##      mu sigma
##   <dbl> <dbl>
## 1  3.14  1.79

# sads
library("sads")
# Estimation. Les données sont tronquées: les espèces observées 0 fois ne sont pas comptées.
fit_sads_lnorm <- fitlnorm(BCI_abd, trunc=0)
fit_sads_lnorm@fullcoef

##  meanlog    sdlog 
## 3.142695 1.787195

#vegan
library("vegan")
fit_vegan_lnorm <- radfit(BCI_abd)
fit_vegan_lnorm

## 
## RAD models, family poisson 
## No. of species 225, total abundance 21457
## 
##            par1      par2     par3    Deviance AIC     
## Null                                  10261.14 11387.97
## Preemption  0.034063                   3788.38  4917.21
## Lognormal   3.3569    1.5738            744.30  1875.13
## Zipf        0.14679  -0.94912          4335.50  5466.33
## Mandelbrot  17.014   -2.0064   15.048   988.02  2120.85
##            BIC     
## Null       11387.97
## Preemption  4920.63
## Lognormal   1881.96
## Zipf        5473.16
## Mandelbrot  2131.10

L’ajustement du modèle de Volkov peut être comparé à celui d’une distribution log-normale.

# Ajustement du modèle de Volkov
fit_volkov <- fitvolkov(BCI_abd)
fit_volkov@fullcoef

##        theta            m            J 
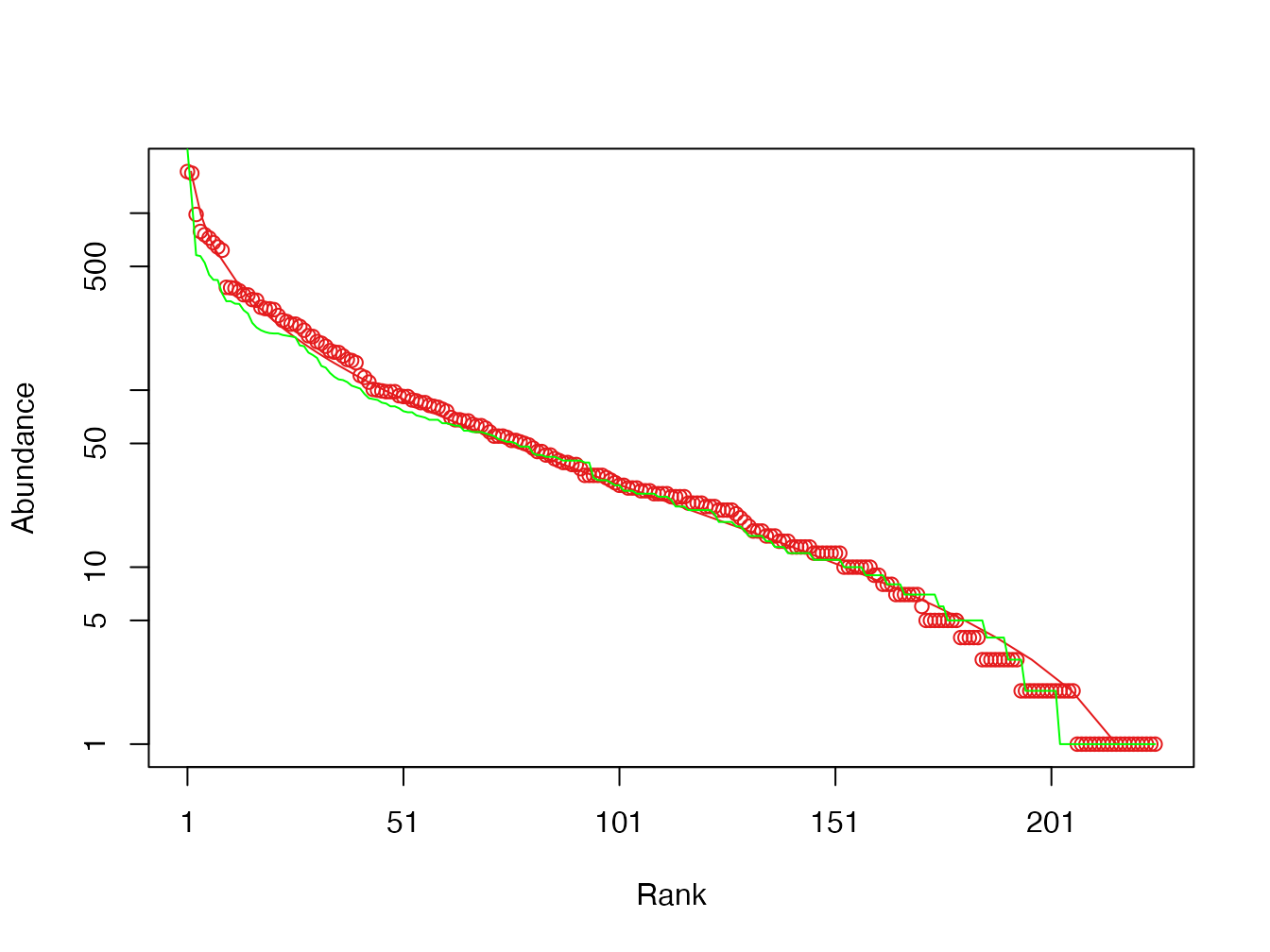
## 4.796210e+01 9.180496e-02 2.145700e+04

Graphiquement, l’ajustement est très proche mais la distribution de Volkov prévoit explicitement des effectifs égaux parce qu’entiers.

# Comparaison graphique des deux modèles. Log-normal en rouge.
plot(as_abundances(BCI_abd), fit_rac = TRUE, distribution="lnorm")
# Volkov en vert
lines(
  sort(
    rvolkov(
      length(BCI_abd), 
      fit_volkov@fullcoef[1], 
      fit_volkov@fullcoef[2], 
      fit_volkov@fullcoef[3]
    ), 
    decreasing=TRUE
  ), 
  col="green"
)

Les vraisemblances sont proches.

# Comparaison des vraisemblances
fit_sads_lnorm@min

## [1] 1157.013

fit_volkov@min

## [1] 1150.182

Les paramètres du modèle de communauté locale de la théorie neutre sont $\theta$, le “nombre fondamental de la biodiversité” égal à deux fois le nombre d’espèces apparaissant par pas de temps dans la méta-communauté, $m$, le taux de migration, et $J$, la taille de la communauté locale (qui n’est pas à proprement parler un paramètre mais une statistique décrivant les données).

La différence entre les logarithmes de vraisemblance des deux modèles en faveur du modèle de Volkov, alors que le nombre de paramètres est le même. L’ajustement est donc meilleur mais la différence est petite et la complexité du modèle et des calculs pour l’estimer ne se justifient pas en général : le modèle de Volkov est très peu utilisé en pratique.

1 Notions de Diversité

3 Mesures classiques de la diversité $\alpha$ ou $\gamma$