1 Notions de Diversité

1.1 Composantes

Figure 1.1: Importance de la richesse (en haut) et de l’équitabilité (en bas) pour la définition de la diversité. Ligne du haut : toutes choses égales par ailleurs, une communauté de 7 espèces semble plus diverse qu’une communauté de 2 espèces. Ligne du bas : à richesse égale, une communauté moins équitable (à gauche) semble moins diverse. Colonne de gauche : une communauté moins riche (en haut) peut sembler plus diverse si elle est plus équitable. Colonne de droite : idem pour la communauté du bas.

Une communauté comprenant beaucoup d’espèces mais avec une espèce dominante n’est pas perçue intuitivement comme plus diverse qu’une communauté avec moins d’espèces, mais dont les effectifs sont proches (figure 1.1, colonne de gauche). La prise en compte de deux composantes de la diversité, appelées richesse et équitabilité, est nécessaire (Whittaker 1965).

1.1.1 Richesse

La richesse (terme introduit par Mcintosh 1967) est le nombre (ou une fonction croissante du nombre) de classes différentes présentes dans le système étudié, par exemple le nombre d’espèces d’arbres dans une forêt.

Un certain nombre d’hypothèses sont assumées plus ou moins explicitement :

• Les classes sont bien connues : compter le nombre d’espèces a peu de sens si la taxonomie n’est pas bien établie. C’est parfois une difficulté majeure quand on travaille sur les micro-organismes ;
• Les classes sont équidistantes : la richesse augmente d’une unité quand on rajoute une espèce, que cette espèce soit proche des précédentes ou extrêmement originale.

L’indice de richesse le plus simple et le plus utilisé est tout simplement le nombre d’espèces \(S\).

1.1.2 Équitabilité

La régularité de la distribution des espèces (équitabilité en Français, evenness ou equitability en anglais) est un élément important de la diversité. Une espèce représentée abondamment ou par un seul individu n’apporte pas la même contribution à l’écosystème. Sur la figure 1.1, la ligne du bas présente deux communautés de 4 espèces, mais celle de droite est beaucoup plus équitable de celle de gauche et semble intuitivement plus diverse. À nombre d’espèces égal, la présence d’espèces très dominantes entraîne mathématiquement la rareté de certaines autres : on comprend donc assez intuitivement que le maximum de diversité sera atteint quand les espèces auront une répartition très régulière.

Un indice d’équitabilité est indépendant du nombre d’espèces (donc de la richesse).

La plupart des mesures de diversité courantes, comme celle de Simpson ou de Shannon, évaluent à la fois la richesse et l’équitabilité.

1.1.3 Disparité

Les mesures classiques de la diversité, dites mesures de diversité neutre (species-neutral diversity) ou taxonomique ne prennent pas en compte une quelconque distance entre classes. Pourtant, deux espèces du même genre sont de toute évidence plus proches que deux espèces de familles différentes. Les mesures de diversité non neutres (chapitre ??) prennent en compte cette notion, qui nécessite quelques définitions supplémentaires (Mouillot et al. 2005; Ricotta 2007).

La mesure de la différence entre deux classes est souvent une distance, mais parfois une mesure qui n’a pas toutes les propriétés d’une distance : une dissimilarité. Les mesures de divergence (Pavoine and Bonsall 2011) sont construites à partir de la dissimilarité entre les classes, avec ou sans pondération par la fréquence.

Si la divergence entre espèces est une distance évolutive comme l’âge du plus récent ancêtre commun, la diversité sera dite phylogénétique. Si c’est une distance fonctionnelle, définie par exemple dans l’espace des traits fonctionnels, la diversité sera dite fonctionnelle.

La disparité (Runnegar 1987), divergence moyenne entre deux espèces (indépendamment des fréquences), ou de façon équivalente la longueur totale des branches d’un arbre phylogénétique, est la composante qui décrit à quel point les espèces sont différentes les unes des autres.

Les mesures de régularité décrivent la façon dont les espèces occupent l’espace des niches (régularité fonctionnelle) ou la régularité dans le temps et entre les clades des évènements de spéciation représentés par un arbre phylogénétique. Ce concept complète celui d’équitabilité dans les mesures classiques : la diversité augmente avec la richesse, la divergence entre espèces, et la régularité (qui se réduit à l’équitabilité quand toutes les espèces sont également divergentes entre elles).

1.1.4 Agrégation

À partir d’une large revue de la littérature dans plusieurs disciplines scientifiques s’intéressant à la diversité (au-delà de la biodiversité), Stirling (2007) estime que les trois composantes, qu’il nomme variété (richesse), équilibre (équitabilité) et disparité, recouvrent tous les aspects de la diversité.

Stirling définit la propriété d’agrégation comme la capacité d’une mesure de diversité à combiner explicitement les trois composantes précédentes. Cela ne signifie pas que les composantes contribuent indépendamment les unes des autres à la diversité (Jost 2010).

1.2 Niveaux de l’étude

La diversité est classiquement estimée à plusieurs niveaux emboîtés, nommés \(\alpha\), \(\beta\) et \(\gamma\) par Whittaker (1960, 320) qui a nommé \(\alpha\) la diversité locale qu’il mesurait avec l’indice \(\alpha\) de Fisher (voir le chapitre ??) et a utilisé les lettres suivantes selon ses besoins.

1.2.1 Diversité \(\alpha\), \(\beta\) et \(\gamma\)

La diversité \(\alpha\) est la diversité locale, mesurée à l’intérieur d’un système délimité. Plus précisément, il s’agit de la diversité dans un habitat uniforme de taille fixe.

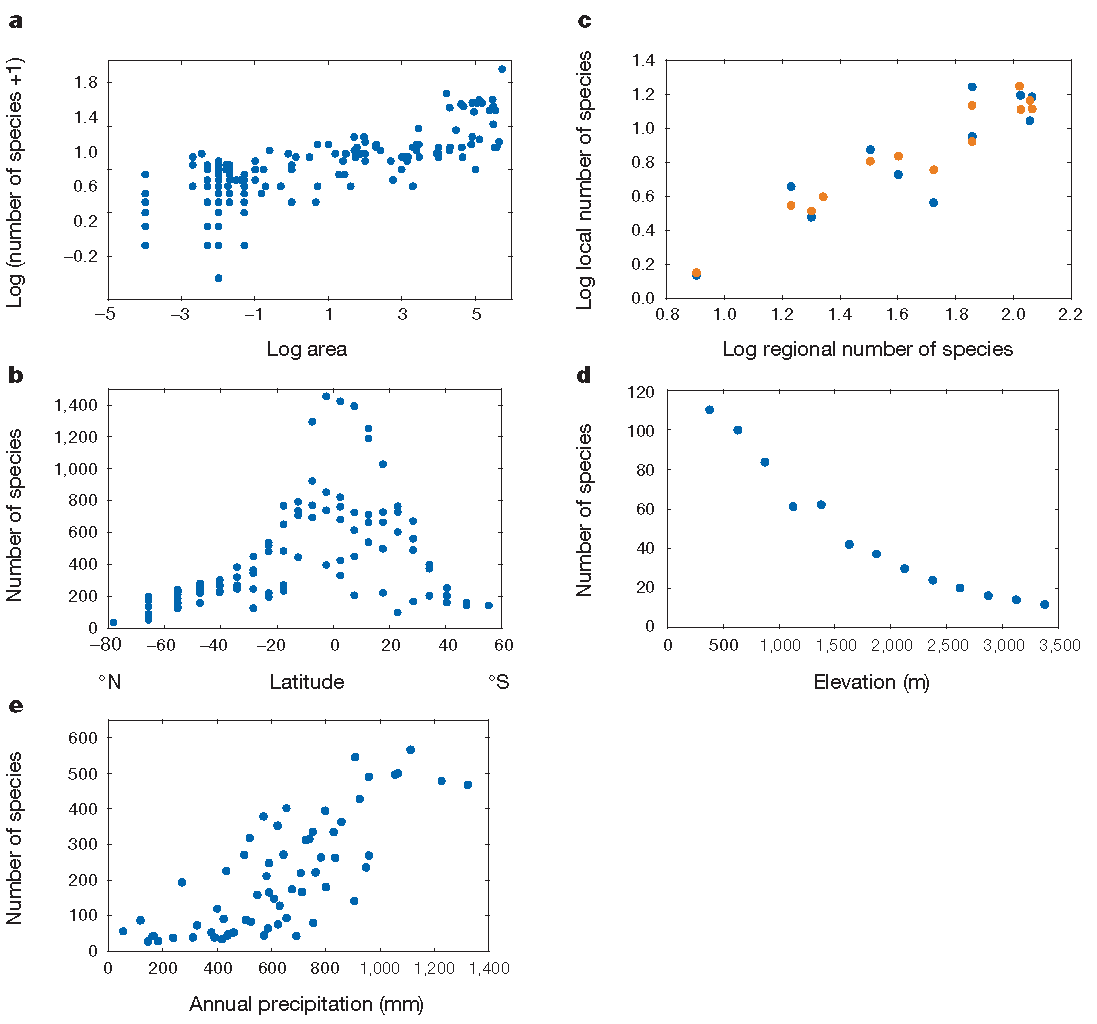
Figure 1.2: Patrons de biodiversité. (a) Le nombre d’espèces de vers de terre augmente en fonction de la surface échantillonnée, de 100 m² à plus de 500000 km² selon la relation d’Arrhenius). (b) Nombre d’espèces d’oiseaux en fonction de la latitude. (c) Relation entre la richesse régionale et la richesse locale. (d) Nombre d’espèces de chauves-souris en fonction de l’altitude dans une réserve au Pérou. (e) Nombre d’espèces de végétaux ligneux en fonction des précipitations en Afrique du Sud.

De façon générale (Gaston 2000), la richesse spécifique diminue avec la latitude (la diversité est plus grande dans les zones tropicales, et au sein de celles-ci, quand on se rapproche de l’équateur), voir figure 1.2 (Gaston 2000, fig. 1). La tendance est la même pour la diversité génétique intraspécifique (Miraldo et al. 2016). La richesse diminue avec l’altitude. Elle est généralement plus faible sur les îles, où elle décroît avec la distance au continent, source de migrations.

La diversité \(\beta\) mesure à quel point les systèmes locaux sont différents. Cette définition assez vague a fait l’objet de nombreux débats (Moreno and Rodríguez 2010).

Enfin, la diversité \(\gamma\) est similaire à la diversité \(\alpha\), prise en compte sur l’ensemble du système étudié. Les diversités \(\alpha\) et \(\gamma\) se mesurent donc de la même façon, mais à différentes échelles.

1.2.2 Décomposition

Whittaker (1977) a proposé sans succès une normalisation des échelles d’évaluation de la biodiversité, en introduisant la diversité régionale \(\varepsilon\) (\(\gamma\) étant réservé au paysage et \(\alpha\) à l’habitat) et la diversité \(\delta\) entre les paysages. Seuls les trois niveaux originaux ont été conservés par la littérature, sans définition stricte des échelles d’observation.

La distinction entre les diversités \(\alpha\) et \(\beta\) dépend de la finesse de la définition de l’habitat. La distinction de nombreux habitats diminue la diversité \(\alpha\) au profit de la \(\beta\). Il est donc important de définir une mesure qui ne dépende pas de ce découpage, donc une mesure cumulative (additive ou multiplicative) décrivant la diversité totale, décomposable en la somme ou le produit convenablement pondérés de toutes les diversités \(\alpha\) des habitats (diversité intra) et de la diversité \(\beta\) inter-habitat.

Nous appellerons communauté le niveau de découpage concernant la diversité \(\alpha\) et méta-communauté le niveau de regroupement pour l’estimation de la diversité \(\gamma\).

1.3 Courbes d’accumulation

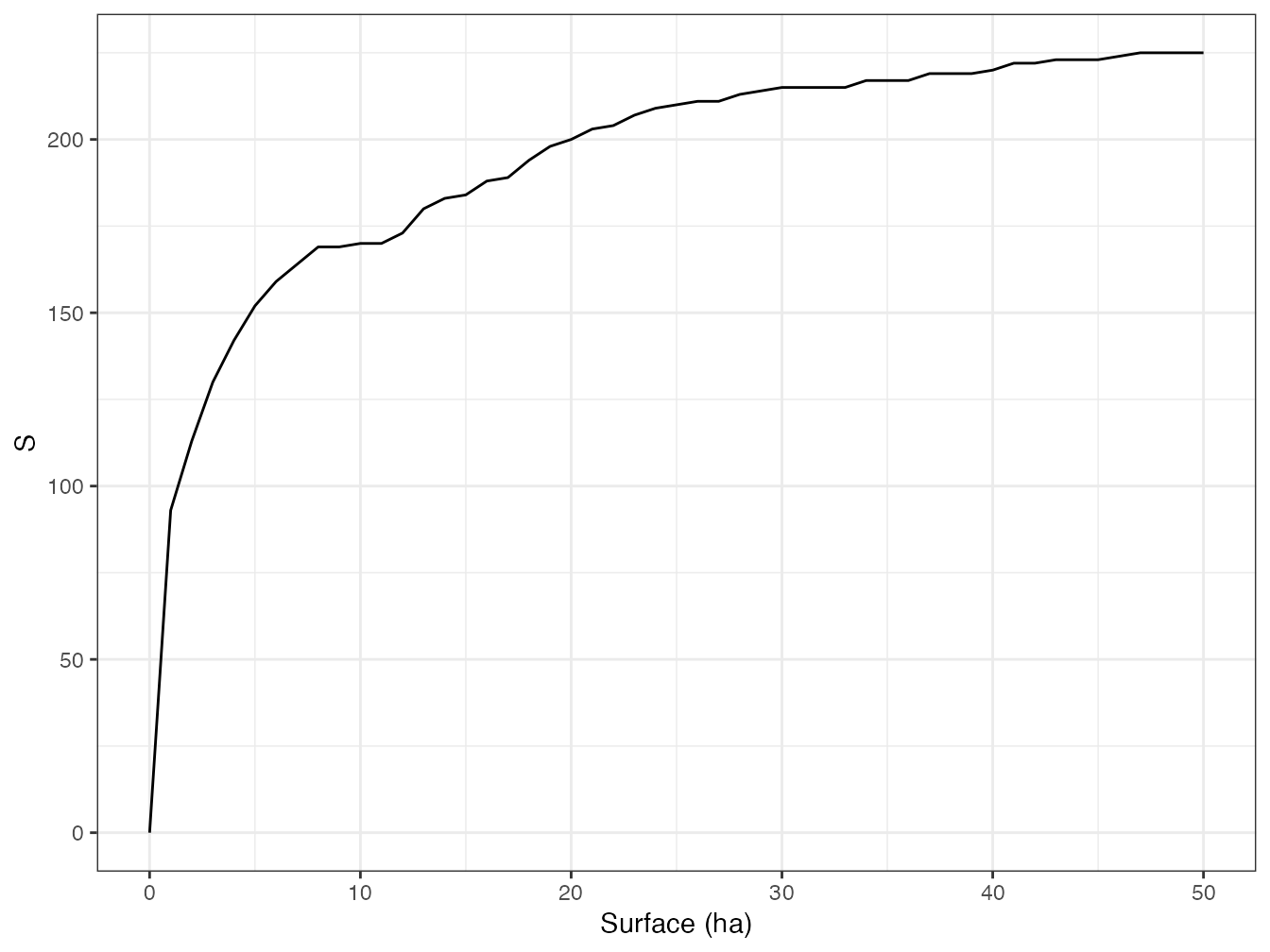
Figure 1.3: Courbe d’accumulation des espèces d’arbres du dispositif de Barro Colorado Island. Le nombre d’espèces est cumulé dans l’ordre des carrés d’un hectare du dispositif.

Evaluer la diversité d’une communauté nécessite en pratique de l’inventorier. Le nombre d’espèces découvertes en fonction de l’effort d’échantillonnage permet de tracer une courbe d’accumulation (SAC : Species Acumulation Curve). Une courbe de raréfaction (Rarefaction Curve) peut être calculée en réduisant par des outils statistiques l’effort d’échantillonnage réel pour obtenir une SAC théorique, libérée des aléas de l’ordre de prise en compte des données.

La figure 1.3 montre l’accumulation des espèces pour les données de BCI. Une SAC peut être tracée en fonction de la surface, du nombre d’individus ou du nombres de placettes d’échantillonnage, selon les besoins.

Code R pour réaliser la figure 1.3 :

library("vegan")
data(BCI)
# Chaque parcelle (ligne) cumule ses abondances à la précédente
cumul <- apply(BCI, 2, cumsum)
# Le nombre d'espèces de chaque parcelle est cumulé 
Richesse <- apply(cumul, 1, function(x) sum(x > 0))
ggplot(
  data.frame(
    A = 0:50, 
    S = c(0, Richesse)
  )
) +
  geom_line(aes(x = A, y = S)) +
  labs(x = "Surface (ha)")

Les courbes d’accumulation peuvent aussi concerner la diversité (voir le chapitre ??), mesurée au-delà du nombre d’espèces.

Plus généralement, une courbe aire-espèces (SAR : Species Area Relationship) représente le nombre d’espèces observées en fonction de la surface échantillonnée (figure ??). Il existe plusieurs façons de prendre en compte cette relation (Scheiner 2003), classables en deux grandes familles (Dengler 2009) :

• Dans une SAR au sens strict, chaque point représente une communauté. La question traitée est la relation entre le nombre d’espèces et la taille de chaque communauté, en lien avec des processus écologiques ;
• Une courbe d’accumulation (SAC) ne représente que l’effet statistique de l’échantillonnage. Pour éviter toute confusion, le terme SAR ne doit pas être utilisé pour décrire une SAC.

1.4 Diversité asymptotique

Augmenter l’effort d’échantillonnage peut permettre d’atteindre un stade où la diversité n’augmente plus : sa valeur est appelée diversité asymptotique. Dans des communautés très diverses comme les forêts tropicales, la diversité asymptotique ne peut en général pas être observée sur le terrain à cause de la variabilité de l’environnement : l’augmentation de la surface inventoriée amène à échantillonner dans des communautés différentes avant d’atteindre la diversité asymptotique de la communauté étudiée. La diversité asymptotique est donc celle d’une communauté théorique qui n’existe généralement pas. En d’autres termes, c’est la diversité d’une communauté dont l’inventaire disponible serait un échantillon représentatif.

Evaluer la diversité asymptotique nécessite d’utiliser des estimateurs de diversité, dont la précision dépend de l’exhaustivité de l’échantillonnage. La diversité peut aussi être estimée pour un effort donné : un hectare de forêt ou 5000 arbres par exemple, ou encore un taux de couverture choisi, qui décrit mieux la qualité de l’échantillonnage.

1.5 Couverture

Le taux de couverture (sample coverage) de l’échantillon est la proportion des espèces découvertes, \[\begin{equation} \tag{1.1} C = \sum^S_{s=1}{{\mathbf 1}\left( n_s > 0 \right) p_s}, \end{equation}\]

où \({\mathbf 1}(\cdot)\) est la fonction indicatrice. Son complément à 1 est appelé déficit de couverture (coverage deficit).

Le déficit de couverture est la probabilité qu’un individu tiré au hasard dans la communauté appartienne à une espèce absente de l’échantillon inventorié. C’est donc aussi la probabilité qu’un individu ajouté à l’inventaire lui ajoute une nouvelle espèce (Good 1953). La pente de la courbe d’accumulation donnant l’espérance du nombre d’espèces en fonction du nombre d’individus (courbe de raréfaction de la figure ??) est donc égale au déficit de couverture (Chao and Jost 2012) :

\[\begin{equation} \tag{1.2} 1 - {\mathbb E}\left[ C\left( n \right) \right] = {\mathbb E}\left[ S\left( n + 1 \right) \right] - {\mathbb E}\left[ S\left( n \right) \right], \end{equation}\]

où \(C(n)\) est le taux de couverture d’un échantillon de taille \(n\) et \(S(n)\) le nombre d’espèces découvertes dans cet échantillon.

Le taux de couverture augmente avec l’effort d’échantillonnage. Plus il est élevé, meilleures seront les estimations de la diversité : la diversité asymptotique est obtenue quand il atteint 1. Les estimateurs de la diversité asymptotique développés plus loin reposent largement sur cette notion pour la correction du biais d’échantillonnage (Dauby and Hardy 2012), c’est-à-dire la sous-estimation systématique de la diversité due aux espèces non observées, qui est un des éléments du biais d’estimation.

Pour comparer la diversité non asymptotique de deux communautés avec le même effort d’échantillonnage, Chao and Jost (2012) montrent que le taux de couverture plutôt que la taille de l’échantillon doit être identique.

1.5.1 Formule des fréquences de Good-Turing

La relation fondamentale entre les fréquences des espèces dans un échantillon est due à Turing et a été publiée par Good (1953). En absence de toute information sur la loi de distribution des espèces, en supposant seulement que les individus sont tirés indépendamment les uns des autres selon une loi multinomiale respectant ces probabilités, la formule de Good-Turing relie la probabilité attendue \({\mathbb E}(p_\nu)\) d’une espèce représentée par \(\nu\) individus au rapport entre les nombres d’espèces représentées \(\nu+1\) fois et \(\nu\) fois :

\[\begin{equation} \tag{1.3} {\mathbb E}\left( p_\nu \right) \approx \frac{(\nu + 1)}{n} \frac{{\mathbb E}\left( f_{\nu+1} \right)}{{\mathbb E}\left( f_\nu \right)}. \end{equation}\]

La variance de \(p_\nu\) est connue :

\[\begin{equation} \tag{1.4} \operatorname{Var}\left( p_\nu \right) \approx {\mathbb E}\left( p_\nu \right) \left[ {\mathbb E}\left( p_{\nu + 1} \right) - {\mathbb E}\left( p_\nu \right) \right]. \end{equation}\]

Elle est petite en comparaison de l’espérance.

Le nombres d’espèces observées \(\nu\) et \(\nu + 1\) fois varient selon l’échantillonnage. La relation de Good-Turing concerne leur espérance mais comme on ne dispose en général que d’un seul inventaire, les espérances \({\mathbb E}(f_\nu)\) et \({\mathbb E}(f_{\nu + 1})\) sont remplacées par les valeurs observées. De même, chacune des espèces observées \(\nu\) fois a une probabilité différente : la relation ne permet pas de prédire précisément, pour un échantillon, les probabilités de chaque espèce.

Ces relations sont le fondement de plusieurs estimateurs de biodiversité présentés plus loin. Les singletons (\(f_{1}\) : le nombre d’espèces observées une seule fois) et les doubletons (\(f_{2}\) : le nombre d’espèces observées deux fois) ont une importance centrale. Pour \(\nu=1\), on a par exemple \(\alpha_1 = 2 f_{2}/(nf_{1})\) : la fréquence d’une espèce typiquement représentée par un singleton est proportionnelle au rapport entre le nombre des doubletons et des singletons. Cet estimateur de probabilité est meilleur que l’estimateur naïf \(1/n\) : en d’autres termes, la distribution des fréquences observées permet d’estimer les probabilités de façon non triviale.

La relation a été précisée (Chiu et al. 2014, eq. 6 et 7a) en limitant les approximations dans les calculs. La seule approximation nécessaire est que les probabilités des espèces représentées le même nombre de fois \(\nu\) varient peu et puissent être considérées toutes égales à \({\mathbb E}(p_\nu)\), ce qui est acceptable puisque la variance de \(p_\nu\) est petite. On peut alors estimer directement \[\begin{equation} \tag{1.5} \hat{p_\nu} = \frac{\left( \nu + 1 \right) f_{\nu + 1}}{\left(n - \nu \right) f_{\nu} + \left(\nu + 1 \right) f_{\nu + 1}} \end{equation}\]

en remplaçant les espérances par les valeurs observées.

Ce nouvel estimateur est à la base de l’estimateur de Chao amélioré et des estimateurs d’entropie de Chao et Jost (sections 3.3.2 et ??).

1.5.2 Estimation du taux de couverture

En posant \(\nu=0\) dans l’équation (1.3), \({\mathbb E}(p_0) \times f_{0} = \pi_0\), la probabilité totale des espèces non représentées, vaut approximativement \(f_{1}/n\). C’est l’estimateur de Good ou Good-Turing, parfois appelé abusivement “formule de Turing” (Z. Zhang and Huang 2007) :

\[\begin{equation} \tag{1.6} \hat{C} = 1 - \frac{f_1}{n}. \end{equation}\]

Cet estimateur est biaisé (Z. Zhang and Huang 2007). En réalité, \[\begin{equation} \tag{1.7} C = 1 - \frac{{\mathbb E}(f_1) - \pi_1}{n}. \end{equation}\]

L’estimateur de Good néglige le terme \(\pi_1\), la somme des probabilités des espèces observées une fois. Ce terme peut être estimé avec un biais plus petit. Chao, Lee, and Chen (1988) puis Z. Zhang and Huang (2007) proposent l’estimateur suivant, qui utilise toute l’information disponible et a le plus petit biais possible :

\[\begin{equation} \tag{1.8} \hat{C} = 1 - \sum^{n}_{\nu = 1}{\left( -1 \right)}^{\nu + 1}{\binom{n}{\nu}}^{-1}f_\nu. \end{equation}\]

Les termes de la somme décroissent très vite avec \(\nu\). En se limitant à \(\nu=1\), l’estimateur se réduit à celui de Good.

Esty (1983), complété par C.-H. Zhang and Zhang (2009), a montré que l’estimateur était asymptotiquement normal et a calculé l’intervalle de confiance de \(\hat{C}\) :

\[\begin{equation} \tag{1.9} C = \hat{C} \pm t^{n}_{1 - \alpha / 2} \frac{\sqrt{f_1 \left( 1 - \frac{f_{1}}{n} \right) + 2f_2}}{n}. \end{equation}\]

Où \(t^{n}_{1 - \alpha / 2}\) est le quantile d’une loi de Student à \(n\) degrés de libertés au seuil de risque \(\alpha\), classiquement 1,96 pour \(n\) grand et \(\alpha = 5\%\).

Un autre estimateur est utilisé dans le logiciel SPADE (Chao and Shen 2010) et son portage sous R, le package spadeR (Chao et al. 2016). Il est la base des estimateurs d’entropie de Chao et Jost (section ??). L’estimation de l’équation (1.7) donne la relation \[\begin{equation} \tag{1.10} \hat{C} = 1 - \frac{f_{1} - \hat{\pi}_1}{n}. \end{equation}\]

Or, \(\hat{\pi}_1 = f_{1} \hat{p}_1\). \(p_1\) peut être estimé par la relation de Good-Turing (1.5), en remplaçant \(f_0\) par l’estimateur Chao1 (3.5). Alors :

\[\begin{equation} \tag{1.11} \hat{C} = 1 - \frac{f_1}{n}(1 - \hat{p}_1) = 1 - \frac{f_1}{n}\left[ \frac{\left( n - 1 \right) f_1}{\left( n - 1 \right) f_1 + 2f_2} \right]. \end{equation}\]

Dans le package divent, la fonction coverage calcule les trois estimateurs (celui de Zhang et Huang par défaut) :

library("divent")
BCI %>% 
  colSums() %>% 
  coverage()

## # A tibble: 1 × 2
##   estimator  coverage
##   <chr>         <dbl>
## 1 ZhangHuang    0.999

Le taux de couverture de BCI est proche de 1 parce que l’inventaire couvre 50 ha. Il est moindre sur les 6.25 ha de la parcelle 6 de Paracou :

paracou_6_abd %>% 
  colSums() %>% 
  coverage()

## # A tibble: 1 × 2
##   estimator  coverage
##   <chr>         <dbl>
## 1 ZhangHuang    0.972

Les estimateurs présentés ici supposent une population de taille infinie (de façon équivalente, les individus sont tirés avec remise). Le cas des populations de taille finie est traité par Chao and Lin (2012) et Hwang, Lin, and Shen (2014).

1.5.3 Complétude

La complétude de l’échantillonnage est la proportion du nombre d’espèces observées : \(f_{>0} / S\). Elle compte simplement les espèces et ne doit pas être confondue avec la couverture qui somme leurs probabilités : le taux de complétude est toujours très inférieur au taux de couverture parce que les espèces non échantillonnées sont les plus rares.

La complétude du même échantillon d’arbres de forêt tropicale que dans l’exemple précédent peut être estimée en divisant le nombre d’espèces observées par le nombre d’espèces estimées (voir section 3.1). À BCI :

bci_abd <- colSums(BCI)
# Espèces observées
(obs <- div_richness(bci_abd, estimator  = "naive"))

## # A tibble: 1 × 3
##   estimator order diversity
##   <chr>     <dbl>     <int>
## 1 naive         0       225

# Richesse estimée
(est <- div_richness(bci_abd))

## # A tibble: 1 × 3
##   estimator   order diversity
##   <chr>       <dbl>     <dbl>
## 1 Jackknife 1     0       244

# Complétude
obs$diversity / est$diversity

## [1] 0.9221311

À Paracou :

# Espèces observées
(obs <- div_richness(colSums(paracou_6_abd), estimator  = "naive"))

## # A tibble: 1 × 3
##   estimator order diversity
##   <chr>     <dbl>     <int>
## 1 naive         0       335

# Richesse estimée
(est <- div_richness(colSums(paracou_6_abd)))

## # A tibble: 1 × 3
##   estimator   order diversity
##   <chr>       <dbl>     <dbl>
## 1 Jackknife 2     0       473

# Complétude
obs$diversity / est$diversity

## [1] 0.7082452

1.6 Le problème de l’espèce

Évaluer la richesse spécifique suppose que les espèces soient définies clairement, ce qui n’est de toute évidence pas le cas (Casetta 2014). Le premier aspect du problème concerne la nature des espèces : réalité naturelle ou seulement représentation simplificatrice. Une analyse historique et philosophique en est faite par Richards (2010). L’autre aspect, avec des conséquences pratiques plus immédiates, concerne leur délimitation. Mayden (1997) recense vingt-deux définitions différentes du concept d’espèce. (Wilkins2011?) estime qu’il n’y a qu’un seul concept d’espèce mais sept définitions, c’est-à-dire sept façons de les identifier, et vingt-sept variations ou mélanges de ces définitions.

La définition historique est celle de morphoespèce, qui classe les espèces selon leurs formes, supposées d’abord immuables. La définition moderne la plus répandue est celle d’espèce biologique (Dobzhansky 1937) : un “groupe de populations naturelles isolées reproductivement les unes des autres” (Mayr 1942). Lorsque les populations d’une espèce sont isolées géographiquement, leur capacité à se reproduire ensemble est toute théorique (et rarement vérifiée expérimentalement). Des populations allopatriques n’ont pas de flux de gènes réels entre elles et peuvent être considérées comme des espèces distinctes selon la définition d’espèce phylogénétique : “le plus petit groupe identifiable d’individus avec un pattern commun d’ancêtres et de descendants” (Cracraft 1983). C’est l’unité génétique détectée par la méthode du coalescent pour la délimitation des espèces (Sukumaran and Knowles 2017). Le nombre d’espèces phylogénétiques est bien supérieur au nombre d’espèces biologiques. Enfin, Van Valen (1976) définit les espèces par la niche écologique qu’elles occupent (à partir de l’exemple des chênes blancs européens) plutôt que par les flux de gènes (permanents entre les espèces distinctes) : la définition écologique d’espèce est proche du concept de complexe d’espèces (ensemble d’espèces voisines échangeant des gènes, Pernès 1984).

Le choix de la définition modifie considérablement sur la quantification de la richesse (Agapow et al. 2004). Des problèmes méthodologiques s’ajoutent aux problèmes conceptuels (Hey 2001) : la séparation ou le regroupement de plusieurs populations ou morphotypes en un nombre plus ou moins grand d’espèces est un choix qui reflète les connaissances du moment et peut évoluer (Barberousse and Samadi 2014).

L’impact du problème de l’espèce sur la mesure de la diversité reste sans solution à ce stade, si ce n’est d’utiliser les mêmes définitions si des communautés différentes doivent être comparées. L’approche phylogénétique (chapitre ??) permet de contourner le problème : si deux taxons très semblables apportent à peine plus de diversité qu’un seul taxon, le choix de les distinguer ou non n’est pas critique.