Biographie
Je suis chercheur en écologie tropicale à l’UMR Amap, enseignant à AgroParisTech et coordinateur du parcours BioGET du master Biodiversité, Ecologie et Evolution (AgroParisTech et Université de Montpellier).
Intérêts
- Ecologie des communautés
- Foresterie tropicale
- Ecologie Statistique
- Développement avec R
Éducation
-
Habilitation à Diriger des Recherches en écologie, 2016
Université de Guyane
-
Doctorat en écologie, 2010
AgroParisTech
-
Ingénieur du Génie Rural, des Eaux et des Forêts, 1999
Ecole Nationale du Génie Rural, des Eaux et des Forêts
-
DEA en économie internationale, 1999
Université Paris I, Panthéon Sorbonne
-
Ingénieur des Travaux des Eaux et Forêts, 1990
Ecole Nationale des Ingénieurs des Travaux des Eaux et Forêts
Experience
Directeur de l’Unité Mixte de Recherche Ecologie des Forêts de Guyane (UMR EcoFoG)
Responsabilités:
- Administration de la Recherche
- Encadrement
- Enseignement (niveaux bac+5 et plus)
- Recherche
Publications sélectionnées
Afficher toutes les publications.
Publications récentes
Commnunications
Logiciels
dbmss est un package R destiné au calcul des statistiques spatiales non paramétriques pour caractériser la structure spatiale d’objets cartographiés. Les principales sont la fonction K de Ripley et ses dérivées et celles utilisées par les économistes comme la fonction Kd de Duranton et Overman et la fonction M de Marcon et Puech.
Cours
*
Ce cours est destiné aux étudiants d’AgroParisTech en dernière année, en dominante d’approfondissement GEEFT. C’est une introduction à la dynamique des forêts tropicales. Les objectifs sont de :
Savoir décrire l’état et la dynamique d’une forêt, Comprendre la dynamique de succession et le rôle des perturbations, Connaître quelques théories fondamentales, Introduire les perturbations anthropiques, avant de voir l’aménagement et l’exploitation de la forêt.
Ce cours est destiné aux étudiants du master d’anthropologie, parcours Humanités environnementales. C’est une introduction à l’écologie forestière. Les objectifs sont de :
Compléter l’introduction générale à l’écologie en présentant les spécificités de l’écologie forestière, Présenter un exemple théorique majeur (niche contre neutralité), Évoquer les fronts de science, en termes d’enjeux et de méthodes.
Ce cours de remise à niveau en statistiques avec R est destiné aux étudiants d’AgroParisTech en dernière année, en dominante d’approfondissement GEEFT
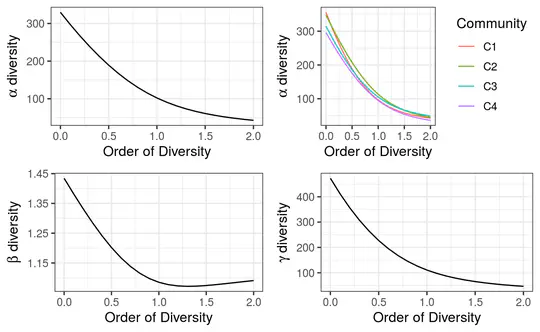
La définition originelle de la biodiversité est le nombre d’espèces d’une communauté. Elle a été élargie de nombreuses façons par des indices souvent ad-hoc.
Ce cours introduit une approche unifiée de la mesure de la biodiversité qui s’appuie sur la théorie de l’information et permet de décrire la biodiversité comme un nombre effectif de catégories (en général, d’espèces) correspondant à la question traitée : la diversité taxonomique quand toutes les espèces sont considérées comme équivalentes, la diversité phylogénétique quand leur proximité évolutive est prise en compte et la diversité fonctionnelle quand la distance entre paires d’espèces ne s’inscrit pas dans un arbre.
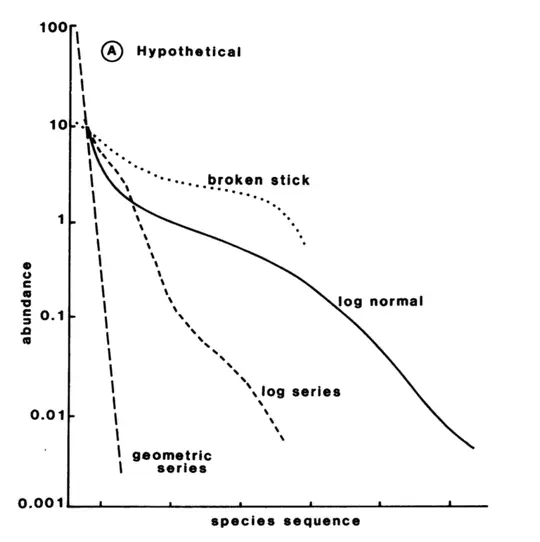
No other general attribute of ecological communities besides species richness has commanded more theoretical and empirical attention than relative species abundance (Hubbell, 2001)
L’objectif du cours est de comprendre les principales distributions d’abondance, maîtriser les différentes représentations et comprendre les relations aires-espèces, à différentes échelles.
Ce cours propose une organisation du travail autour de R et RStudio pour, au-delà des statistiques, rédiger des documents efficacement avec R Markdown, aux formats variés (mémos, articles scientifiques, mémoires d’étudiants, livres, diaporamas), créer son site web et des applications R en ligne (Shiny), produire des packages et utiliser R pour l’enseignement.