Calculate the deformed logarithm of order q.
ln_q(x, q)Arguments
- x
A numeric vector or array.
- q
A number.
Value
A vector of the same length as x containing the transformed values.
Details
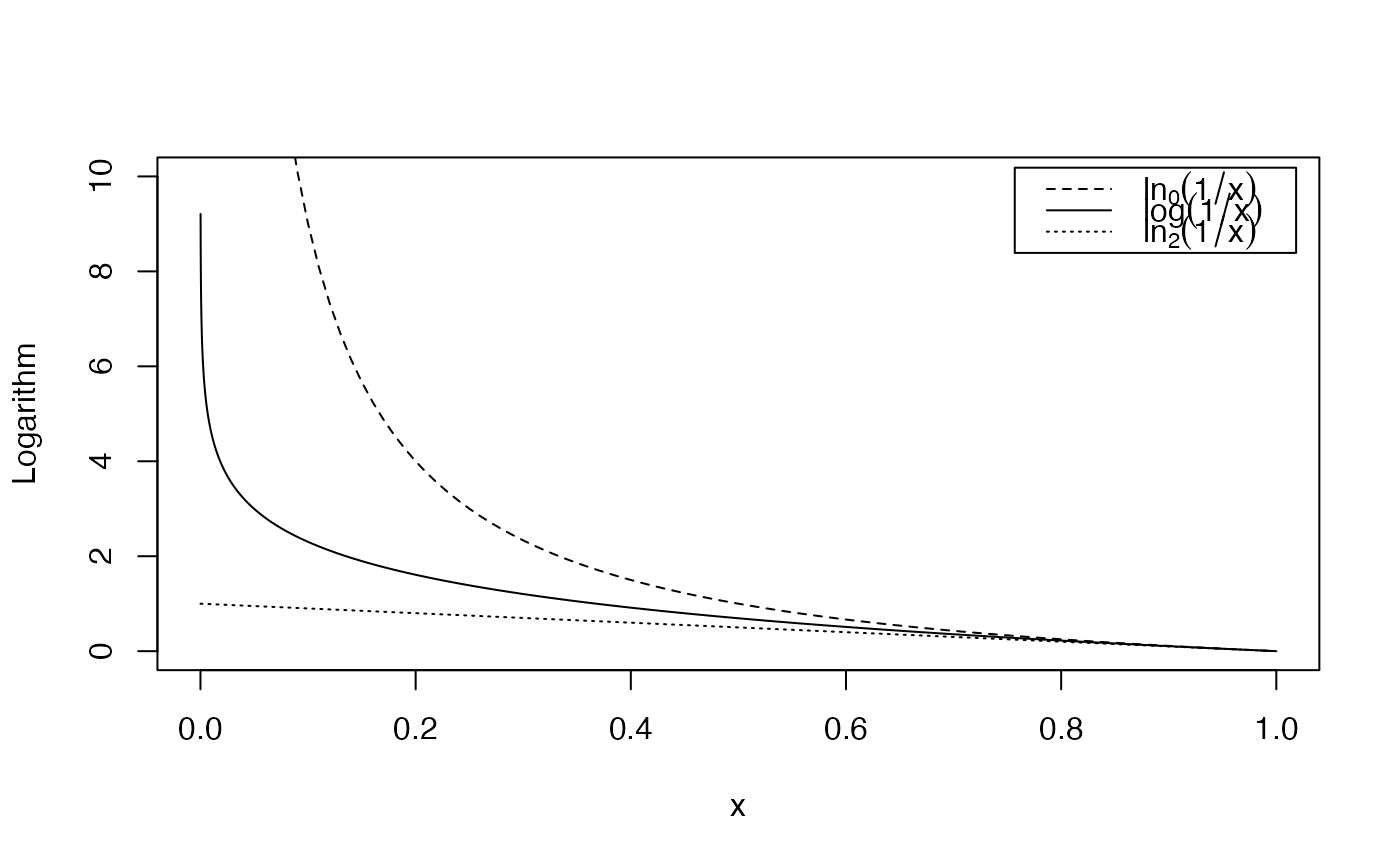
The deformed logarithm (Tsallis 1994) is defined as \(\ln_q{x}=\frac{(x^{(1-q)}-1)}{(1-q)}\).
The shape of the deformed logarithm is similar to that of the regular one. \(\ln_1{x}=\log{x}\).
For \(q>1\), \(\ln_q{(+\infty)}=\frac{1}{(q-1)}\).
References
Tsallis C (1994). “What Are the Numbers That Experiments Provide?” Química Nova, 17(6), 468--471.
Examples
curve(ln_q( 1/ x, q = 0), 0, 1, lty = 2, ylab = "Logarithm", ylim = c(0, 10))
curve(log(1 / x), 0, 1, lty = 1, n =1E4, add = TRUE)
curve(ln_q(1 / x, q = 2), 0, 1, lty = 3, add = TRUE)
legend("topright",
legend = c(
expression(ln[0](1/x)),
expression(log(1/x)),
expression(ln[2](1/x))
),
lty = c(2, 1, 3),
inset = 0.02
)
