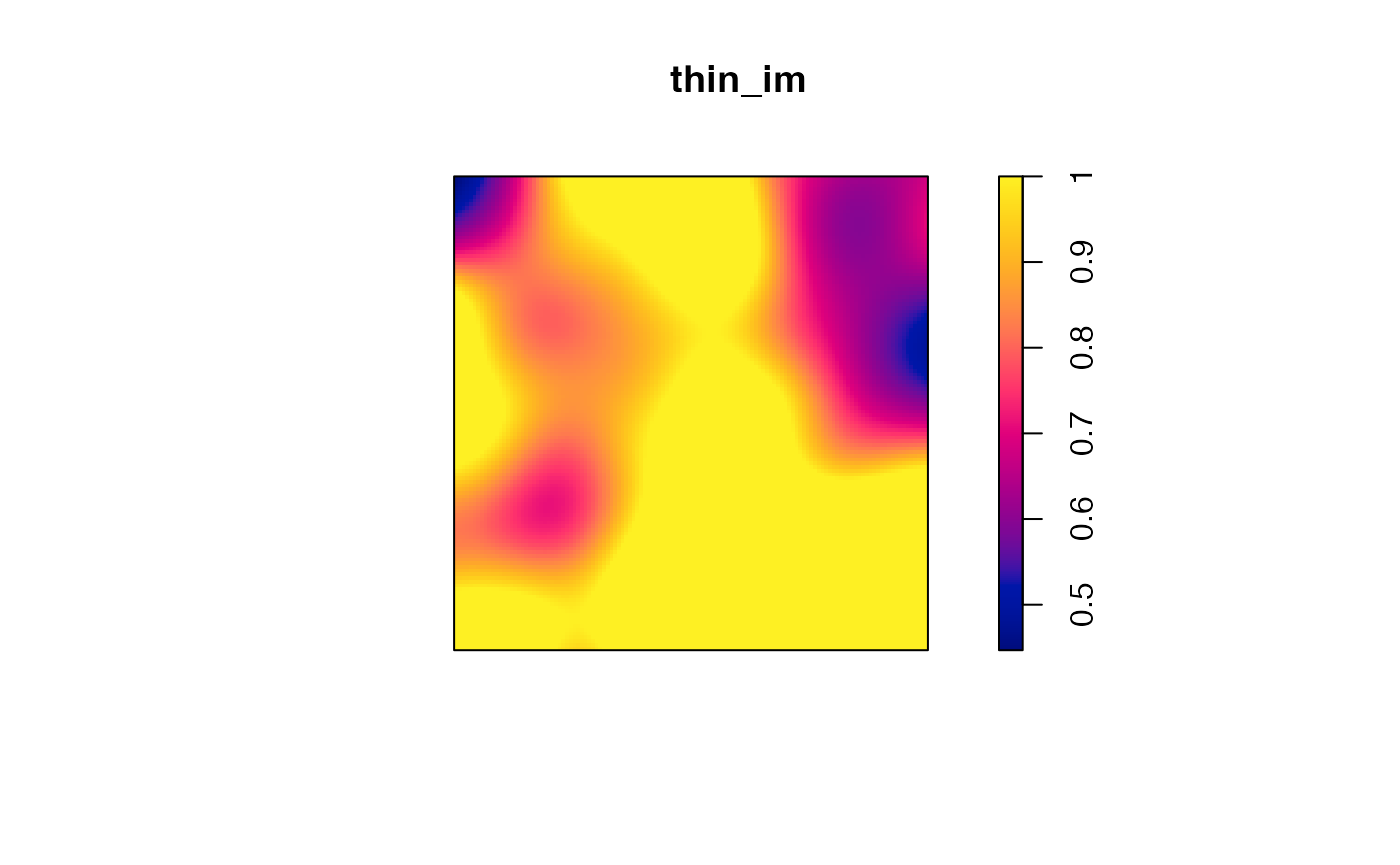Skip to contents

Random communities

Source: vignettes/articles/simulations.Rmd
simulations.Rmd

The package proposes several functions to simulate random communities.

Simulating abundances according to classical models

The classical models of ecology are implemented in divent in the rcommunity() function.

Arguments are :

  • n: the number of communities to draw.
  • size: the number of individuals to draw in each community.
  • species_number: the number of species.
  • distribution: the distribution of species abundances.

Distributions may be “lnorm” (log-normal), “lseries” (log-series), “geom” (geometric) or “bstick” (broken stick):

  • log-normal (“lnorm”) distributions (Preston 1948) require argument sd_lnorm to set the standard deviation of the log-abundances. The expectation of the distribution is computed from the other arguments.
  • log-series (“lseries”) distributions (Fisher, Corbet, and Williams 1943) rely on the fisher_alpha argument. They ignore species_number because the number of species is given by fisher_alpha and size.
  • geometric (“geom”) distributions (Motomura 1932) have argument prob_geom. This distribution is not stochastic.
  • MacArthur’s broken stick (“bstick,” MacArthur 1957) has no argument.

The probability distribution is first drawn, once. Abundances are then drawn in n multinomial distributions, with respect to the probabilities and size.

Example: a single log-normal community with 300 species and standard deviation equal to 2 is drawn and plotted:

library("dplyr")  # for `%>%`
library("divent")
rcommunity(1, size = 1E4, species_number = 300, distribution = "lnorm") %>% 
  # Rank-abundance plot
  autoplot()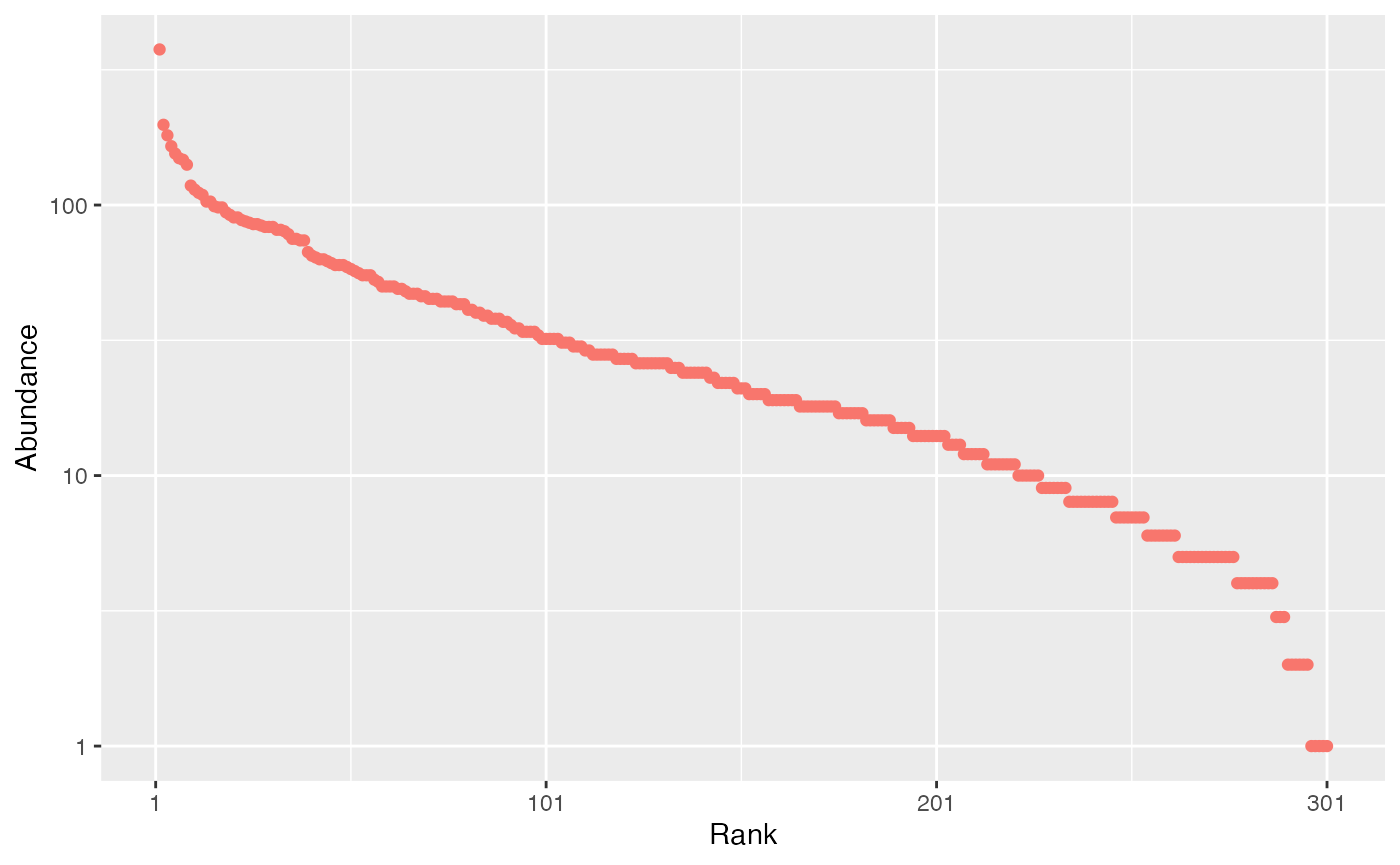

Bootstrapping an observed abundance distribution

Bootstrapping allows drawing many community according to the same probability distribution according to a multinomial law with respect to the probabilities and size. This is useful to compute confidence intervals of any statistics of the distribution.

Arguments are :

  • n: the number of communities to draw.
  • size: the number of individuals to draw in each community.
  • prob or abd: a numeric vector containing probabilities or abundances. One of them must be given, the other one must be NULL.
  • bootstrap: defines the technique used:
    • “Marcon2012”: following Marcon et al. (2012), abundances are just normalized to obtain probabilities. If prob is given rather than abd, these probabilities are used.
    • “Chao2013” or “Chao2015” (by default): based on the observed abundances (abd must be given), the actual probability distribution is estimated following Chao, Wang, and Jost (2013) or Chao and Jost (2015). Observed frequencies (normalized abundances) are not directly used as estimators of the probabilities: abundant species are correctly estimated but rare species are either overestimated or unobserved. A model based on sample coverage is used to correct this issue. The estimator of sample coverage is chosen by the argument coverage_estimator: the sum of observed probabilities equals the sample coverage. The number of unobserved species is estimated and their distribution (their probabilities sum to the coverage deficit) is arbitrary set as uniform (“Chao2013”) or geometric (“Chao2015”).

Example: a community based on the subplot 1 of Paracou plot 6 is drawn and its distribution is compared to the observed frequencies.

library("ggplot2") # for `labs()`
# Draw a large community to avoid sample bias
rcommunity(1, size = 1E6, abd = as.numeric(paracou_6_abd[1, ])) %>% 
  # Compute the probabilities
  as_probabilities() %>% 
  # Rename the distribution
  mutate(site = "bootstrap") %>% 
  # Compare to the original distribution
  bind_rows(as_probabilities(paracou_6_abd[1, ])) %>% 
  autoplot() +
  labs(color = "Distribution")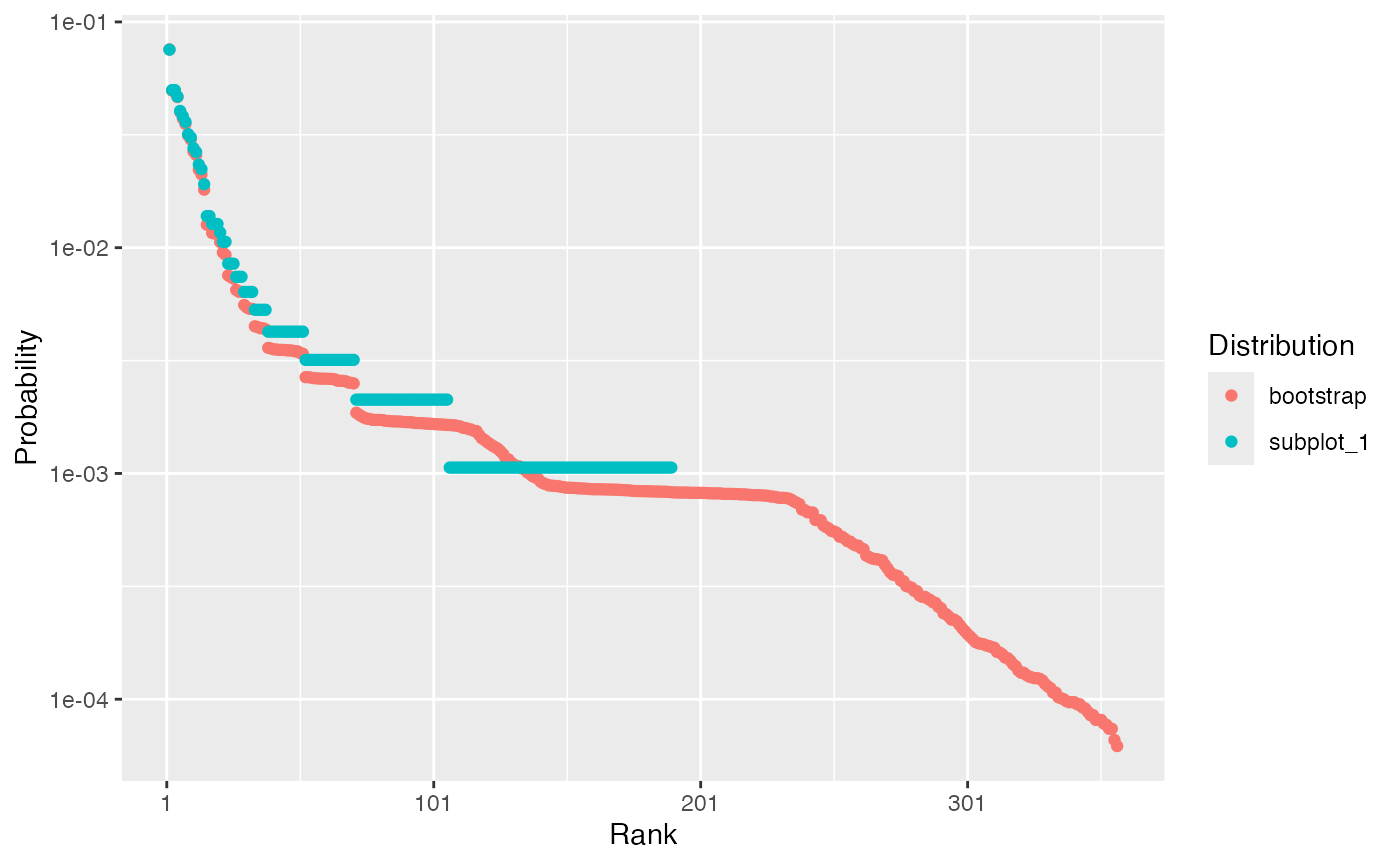

The probabilities of abundant species are not modified. The probabilities of rare species is smaller than their frequencies and more than a hundred species are added.

Simulating spatialized communities

Communities

Spatialized communities include the location of individuals in a window. The abundance distribution is drawn according to the same arguments as in rcommunity().

Additional arguments allow choosing:

  • the window: win must be an owin object from the spatstat.geom package. Default is a square window whose side length is 1.
  • the species names: species_names is a character vector with the species names. They may be generated automatically.
  • the spatial distribution of the points in argument spatial, i.e. the point process used to draw their location:
    • “Binomial” draws points uniformly in the window.
    • “Thomas” draws aggregated points: thomas_mu is the average number of points per cluster and thomas_scale the standard deviation of random displacement (along each coordinate axis) of a point from its cluster center.
  • the weight_distribution of the points sets their sizes:
    • “Uniform”: a uniform distribution between w_min and w_max. This is the default distribution, with w_min = w_max = 1.
    • “Weibull”: parameters are w_min (minimum size), weibull_scale (the scale parameter) and shape (the shape parameter).
    • “Exponential”: argument w_mean is the mean weight, i.e. the negative of the inverse of the decay rate.

Example: a random community is drawn and mapped. It contains 100 trees of 5 species. Their spatial distribution is aggregated and their size distribution is exponential (with default parameters).

rspcommunity(
  1, 
  size = 100, 
  species_number = 5, 
  spatial = "Thomas", 
  weight_distribution = "Exponential"
) %>% 
  autoplot()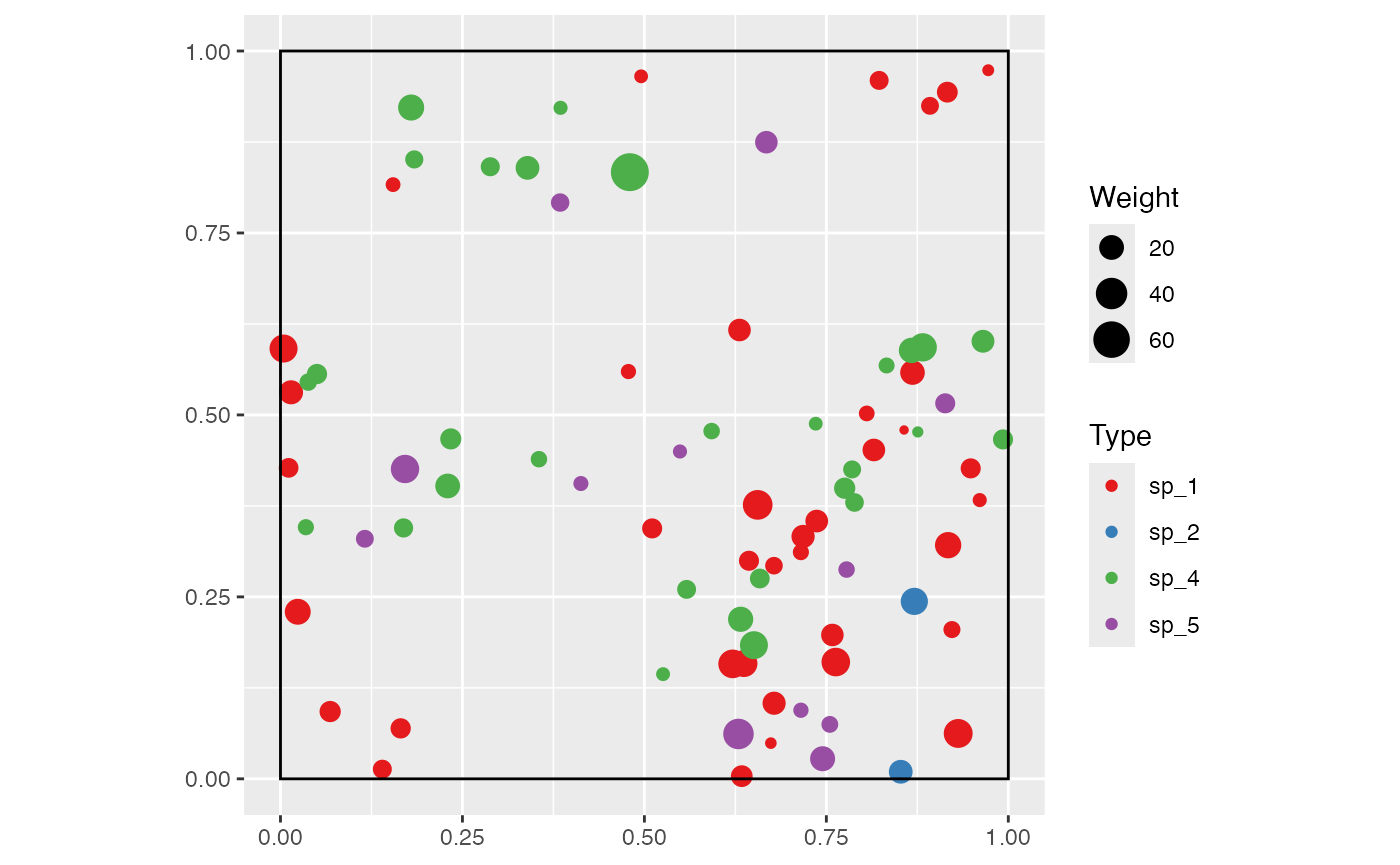

Species

To simulate communities more accurately, species can be drawn one by one. This way, spatial structures and size distributions can be chosen for each species.

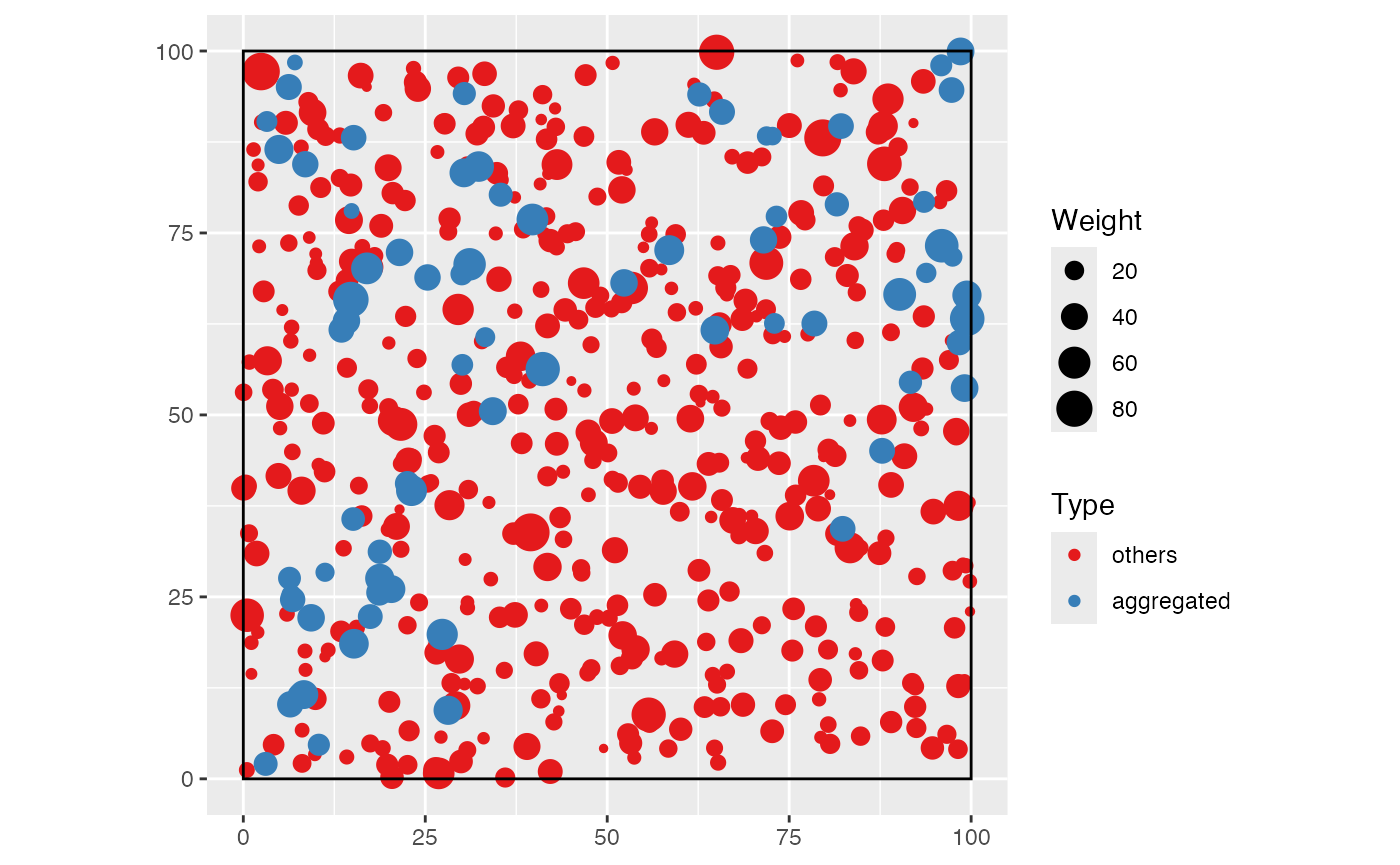
The following example shows how to do it: a 1-ha forest made of an aggregated species of interest and undifferentiated other ones. rspcommunity() is called with arguments n = 1 and species_number = 1. A list is of point patterns is obtained and superimposed to make a single wmppp object.

library("spatstat") # for `square()`
library("dbmss")    # for `superimpose.wmppp()`
library("ggplot2")  # for `labs()`
library("dplyr")    # for `%>%`
library("divent")
# A 1-ha window
the_win <- square(100, unitname = c("meter", "meters"))
# Simulate species
the_species <- do.call(
  superimpose,
  list(
    rspcommunity(
      # A "grey" species, i.e. all individuals of species out of focus
      n = 1, species_number = 1, species_names = "others", size = 500,
      # Spatial features: binomial distribution
      win = the_win, spatial = "Binomial",
      # Size distribution
      weight_distribution = "Exponential", w_min = 10, w_mean = 15),
    rspcommunity(
      # The species of interest
      n = 1, species_number = 1, species_names = "aggregated", size = 50,
      # Spatial features: aggregated distribution
      win = the_win, spatial = "Thomas", thomas_scale = 10, thomas_mu = 20,
      # Size distribution
      weight_distribution = "Weibull", weibull_scale = 30, weibull_shape = 2,
      w_min = 10
    )
  )
)
# Map the simulated community
autoplot(the_species) +
  labs(color = "Species", size = "Diameter")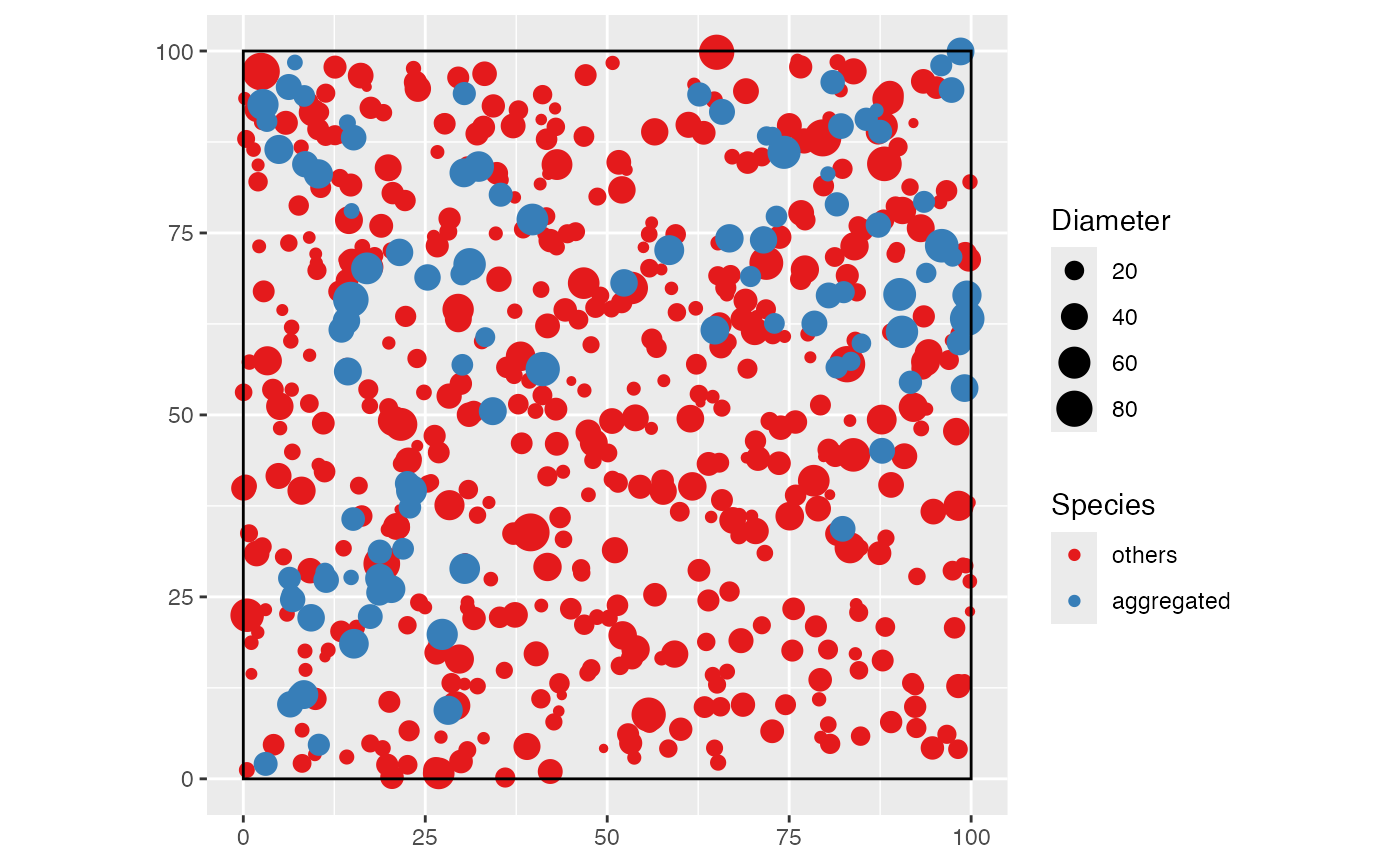

Post-simulation processing of such spatialized communities may be for instance thinning to reduced the local average basal area.

# Basal area
G <- (spatstat.geom::marks(the_species)$PointWeight)^2 * pi / 4E4
sum(G)
## [1] 41.90301
# Density
G_density <- density(the_species, sigma = 10, weights = G)
plot(G_density)

# Thinning: the target is at most 40m² locally
target <- mean(G_density) * 40 / sum(G)
thin_im <- G_density
thin_im$v <- pmin(pmax(target / G_density$v, 0), 1)
# Plot the thinning probability
plot(thin_im)

# Plot the thinned community 
rthin(
  the_species,
  P = thin_im
) %>% autoplot()

Chao, Anne, and Lou Jost. 2015. “Estimating Diversity and Entropy Profiles via Discovery Rates of New Species.” Methods in Ecology and Evolution 6 (8): 873–82. https://doi.org/10.1111/2041-210X.12349.
Chao, Anne, Yi-Ting Wang, and Lou Jost. 2013. “Entropy and the Species Accumulation Curve: A Novel Entropy Estimator via Discovery Rates of New Species.” Methods in Ecology and Evolution 4 (11): 1091–1100. https://doi.org/10.1111/2041-210x.12108.
Fisher, Ronald Aylmer, A. Steven Corbet, and Carrington Bonsor Williams. 1943. “The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population.” Journal of Animal Ecology 12: 42–58. https://doi.org/10.2307/1411.
MacArthur, Robert H. 1957. “On the Relative Abundance of Bird Species.” Proceedings of the National Academy of Sciences of the United States of America 43 (3): 293–95. https://doi.org/10.1073/pnas.43.3.293.
Marcon, Eric, Bruno Hérault, Christopher Baraloto, and Gabriel Lang. 2012. “The Decomposition of Shannon’s Entropy and a Confidence Interval for Beta Diversity.” Oikos 121 (4): 516–22. https://doi.org/10.1111/j.1600-0706.2011.19267.x.
Motomura, I. 1932. “On the statistical treatment of communities.” Zoological Magazine 44: 379–83.
Preston, F. W. 1948. “The Commonness, and Rarity, of Species.” Ecology 29 (3): 254–83. https://doi.org/10.2307/1930989.