4 Diversité jointe
Le tableau de contingence des secteurs et des pays permet de décomposer la diversité totale et d’en tirer plusieurs informations intéressantes. Pour conserver les propriétés de la décomposition, la diversité et l’ubiquité ne seront pas transformées en spécialisation et concentration.
Cutrini (2010) a appelé localisation globale l’information mutuelle du tableau de contingence, c’est-à-dire la concentration relative des secteurs, égale à la spécialisation relative des régions mesurés par la divergence de Kullback-Leibler (l’indice relatif de Theil). Ce n’est qu’une partie de l’information fournie par les données, la diversité ou l’ubiquité \(\beta\), et cette approche n’est valide qu’à l’ordre 1. La diversité jointe exploite toute l’information en combinant diversités ou ubiquités \(\alpha\), \(\beta\) (formant ensemble la diversité \(\gamma\)) et redondance.
4.1 Diversité (spécialisation) des pays
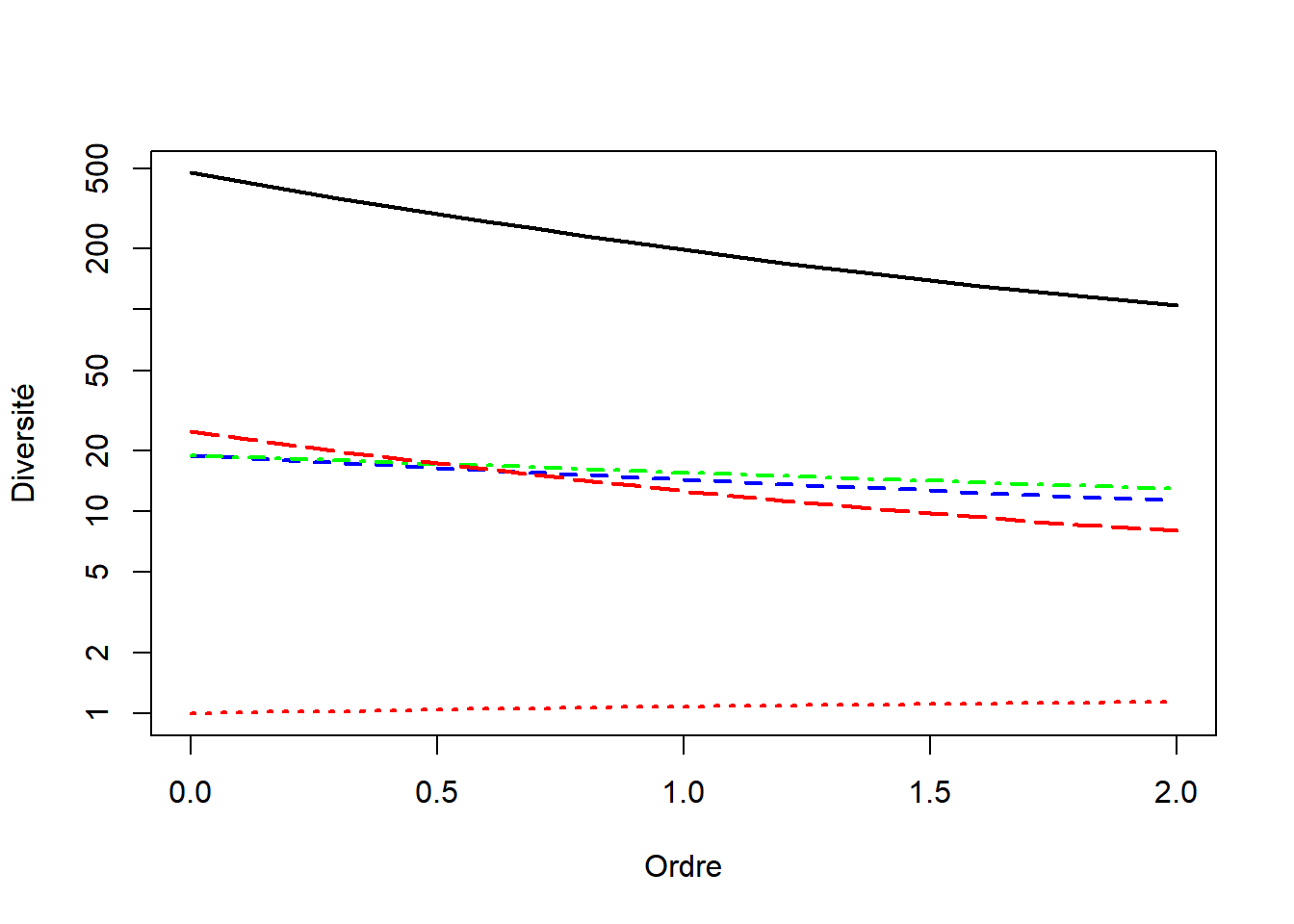
Figure 4.1: Profils de diversité des pays européens: diversité jointe (courbe pleine, noire), diversité \(\alpha\) intra-pays (pointillés bleus), nombre effectif de pays (diversité \(\beta\), spécialisation relative moyenne: pointillés courts, rouges), diversité de l’Europe (\(\gamma\): pointillés longs, verts) et redondance des pays (pointillés longs, rouges). L’échelle de la diversité est logarithmique.
La diversité jointe est décomposée en produit de la diversité \(\alpha\), le nombre effectif de secteurs industriels par pays, de la diversité \(\beta\), le nombre effectif de pays, et de la redondance, le nombre de réplications de ces pays effectifs. La diversité \(\gamma\), produit de \(\alpha\) et \(\beta\) est celle l’Europe. La décomposition est valide à tous les ordres de diversité, et présentée sous la forme de profils (figure 4.1).
Les profils sont tracés sur une échelle logarithmique parce que les valeurs sont d’ordres de grandeurs différents et aussi parce que la décomposition multiplicative devient additive sous cette forme: la hauteur de la diversité jointe sur la figure est la somme des hauteurs des diversités \(\alpha\) et \(\beta\) et de la redondance.
La diversité de l’Europe (\(\gamma\), courbe verte) a déjà été présentée en figure 3.2. Elle est très proche de la diversité \(\alpha\), intra-pays (courbe bleue): le nombre effectif de pays (\(\beta\), spécialisation relative, courbe rouge) varie de 1 (à l’ordre 0) à 1.1 à l’ordre 2. Cette valeur est très faible : le maximum possible est le nombre de pays, 25, s’ils ne partagent aucun secteur; en fait seulement 19 parce que le nombre de secteurs est ici inférieur au nombre de pays. Les pays présentent donc un certain niveau de spécialisation absolue, mais il est identique à celui de l’Europe entière : leur spécialisation relative est très faible. La spécialisation relative augmente avec l’ordre considéré, c’est-à-dire en négligeant progressivement les secteurs de petite taille: les pays sont un peu plus différents entre eux en ne considérant que les secteurs les plus importants.
La redondance des pays est par conséquent élevée : de 25 à l’ordre 0 (tous les pays abritent tous les secteurs) à 8 à l’ordre 2.
4.2 Ubiquité (concentration) des secteurs
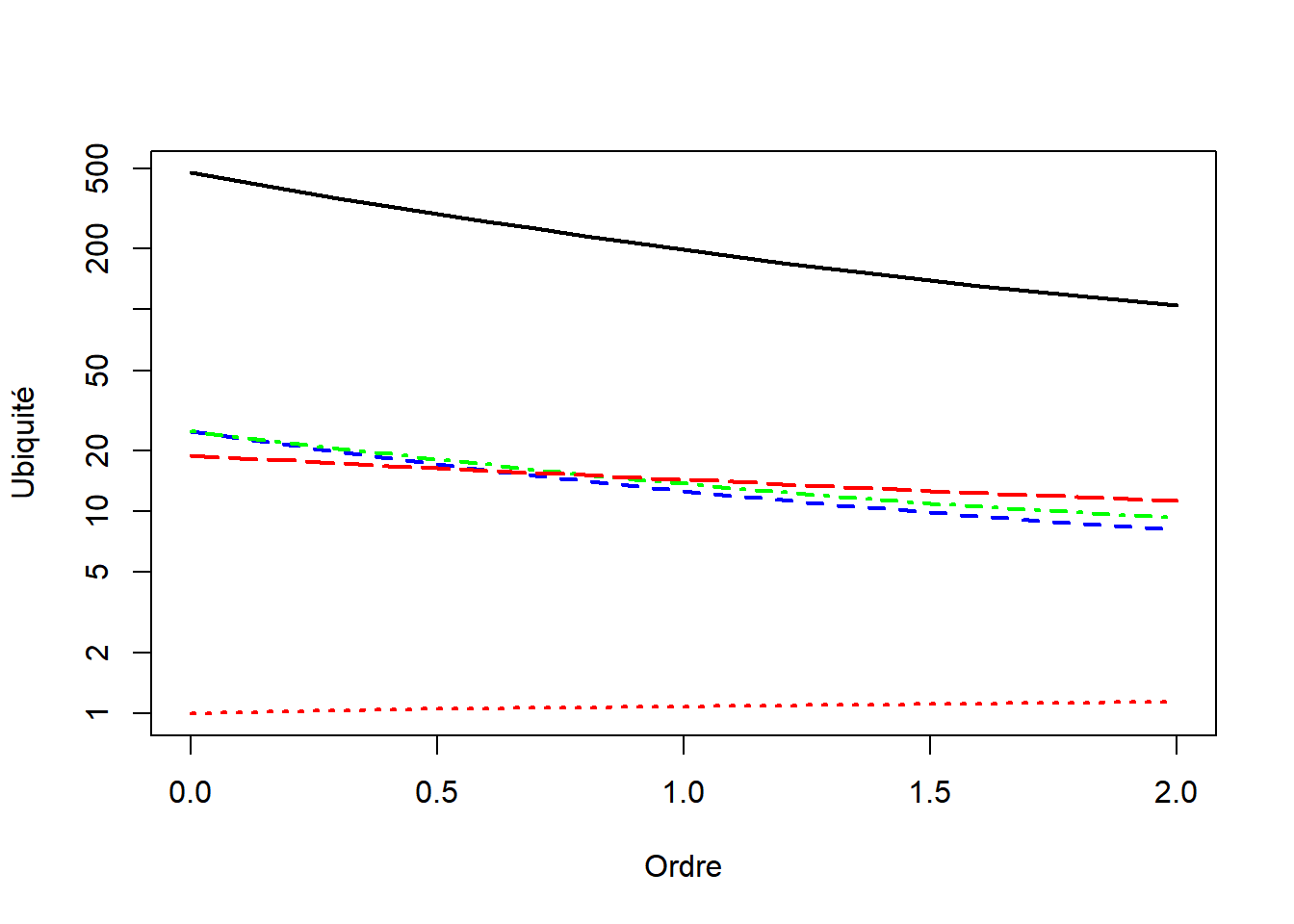
Figure 4.2: Profils d’ubiquité des secteurs industriels: diversité jointe (courbe pleine, noire), ubiquité \(\alpha\) intra-sectorielle (pointillés bleus), nombre effectif de secteurs (concentration relative, ubiquité \(\beta\): pointillés courts, rouges), ubiquité de l’industrie entière (\(\gamma\): pointillés longs, verts) et redondance des secteurs (pointillés longs, rouges). L’échelle est logarithmique.
La figure 4.2 montre la décomposition de l’ubiquité des secteurs industriels.
Les résultats sont similaires à ceux de la spécialisation. Les secteurs sont concentrés dans l’absolu mais leur concentration relative est très faible et la redondance est grande.
Cette grande redondance des pays et des secteurs montre qu’à ce niveau d’agrégation des données, l’industrie européenne a une structure peu variable entre pays ou entre secteurs.