3 Concentration spatiale et spécialisation
Les méthodes présentées jusqu’ici, issues de la physique et de l’écologie statistiques, ont des applications intéressantes en économie. Deux questions seront traitées : celle de la mesure de la concentration spatiale des activités économiques et celle de la décomposition de la localisation globale.
La concentration spatiale des activités économiques est un sujet important de la littérature (Combes et Gobillon 2015). La première étape de la compréhension des phénomènes économiques en jeu est la caractérisation de la concentration. Une étape majeure a été franchie par Ellison et Glaeser (1997) qui ont posé clairement le principe d’une mesure relative (la distribution géographique d’un secteur industriel est comparée à celle de la taille des régions où elle est considérée, principe résumé sous le titre d’approche du jeu de fléchettes) et celui du test statistique de la distribution observée contre sa valeur sous une hypothèse nulle appropriée : une distribution uniforme et indépendante. Ces caractéristiques font défaut à des indices de concentration antérieurs, comme l’indice de Gini (Gini 1912; Ceriani et Verme 2012) dont la valeur observée ne peut être comparée qu’à ses extrêmes possibles.
La statistique centrale de l’indice d’Ellison et Glaeser pour le secteur \(s\) est, avec nos notations, \(G_s=\sum_i{(p_{i|s} - p_i)^2}\), c’est-à-dire la somme des carrés des écarts entre la part du pays \(i\) dans l’effectif total du secteur \(s\) et la part du pays \(i\) dans l’industrie, tous secteurs confondus. En termes mathématiques, \(G\) est la distance \(L^2\) entre la distribution observée du secteur \(s\) et sa distribution attendue, celle de l’industrie en général.
L’indice relatif de Theil (1967) est parfois utilisé dans le même objectif (Cutrini 2009): il mesure aussi l’écart entre la distribution observée et la distribution attendue, mais avec une autre métrique : la divergence de Kullback-Leibler.
L’entropie HCDT permet d’unifier et étendre ces approches. La concentration, absolue puis relative, sera envisagée en premier. La spécialisation suivra.
3.1 Concentration spatiale
3.1.1 Ubiquité et concentration absolue
L’ubiquité du secteur \(s\), \(^{q}D(\mathbf{p_{i|s}})\) est le nombre effectif de pays qu’il occupe. L’ubiquité peut être calculée pour n’importe quel niveau de regroupement sectoriel, ici pour l’industrie entière (code NACE C) ou par secteur détaillé. Un profil d’ubiquité peut être tracé pour chaque secteur. Aux faibles ordres, l’ubiquité donne une grande importance aux pays peu occupés. À \(q=0\), l’ubiquité est simplement le nombre de pays dans lesquels le secteur est présent. Aux grands ordres, seuls les pays occupés majoritairement contribuent à l’ubiquité.
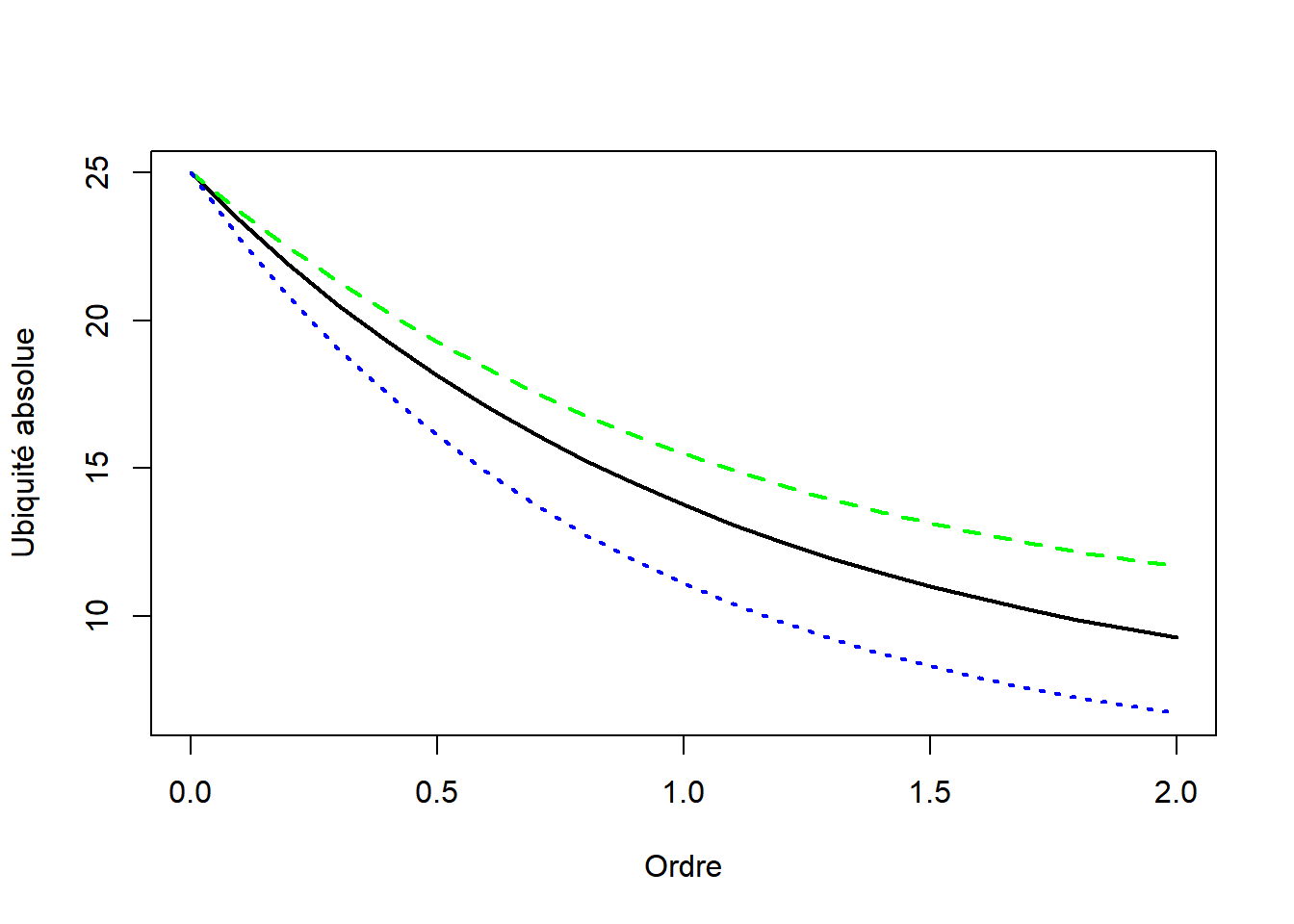
Figure 3.1: Profils d’ubiquité absolue de l’industrie (courbe pleine, noire), du secteur C10 (pointillés longs, verts) et du secteur C20 (pointillés courts, bleus)
La figure 3.1 présente les profils d’ubiquité de l’industrie entière et des secteurs C10 (Manufacture de produits alimentaires) et C20 (Manufacture de produits chimiques) qui s’écartent le plus, parmi tous les secteurs étudiés, de l’industrie entière. L’ubiquité est mesurée en nombre effectifs de pays. Les secteurs sont présents dans tous les pays (les données sont très agrégées) donc l’ubiquité d’ordre 0 est toujours égale au maximum possible, 25. À l’ordre 2, à l’autre extrémité des courbes, 9.3 pays occupés par le même nombre de personnes suffiraient pour obtenir le même niveau d’ubiquité que celui observé pour l’ensemble de l’industrie.
L’ubiquité est la notion opposée à celle de concentration. Une transformation simple des valeurs d’ubiquité permet de les traduire en niveau de concentration plus conformes à la culture économique. Le complément de l’ubiquité au nombre de pays est une bonne mesure de la concentration en tant que nombre effectif de pays délaissés par le secteur étudiés. Il peut être normalisé par le nombre de pays moins 1 pour obtenir une valeur entre 0 et 1 présentée en figure 3.2.
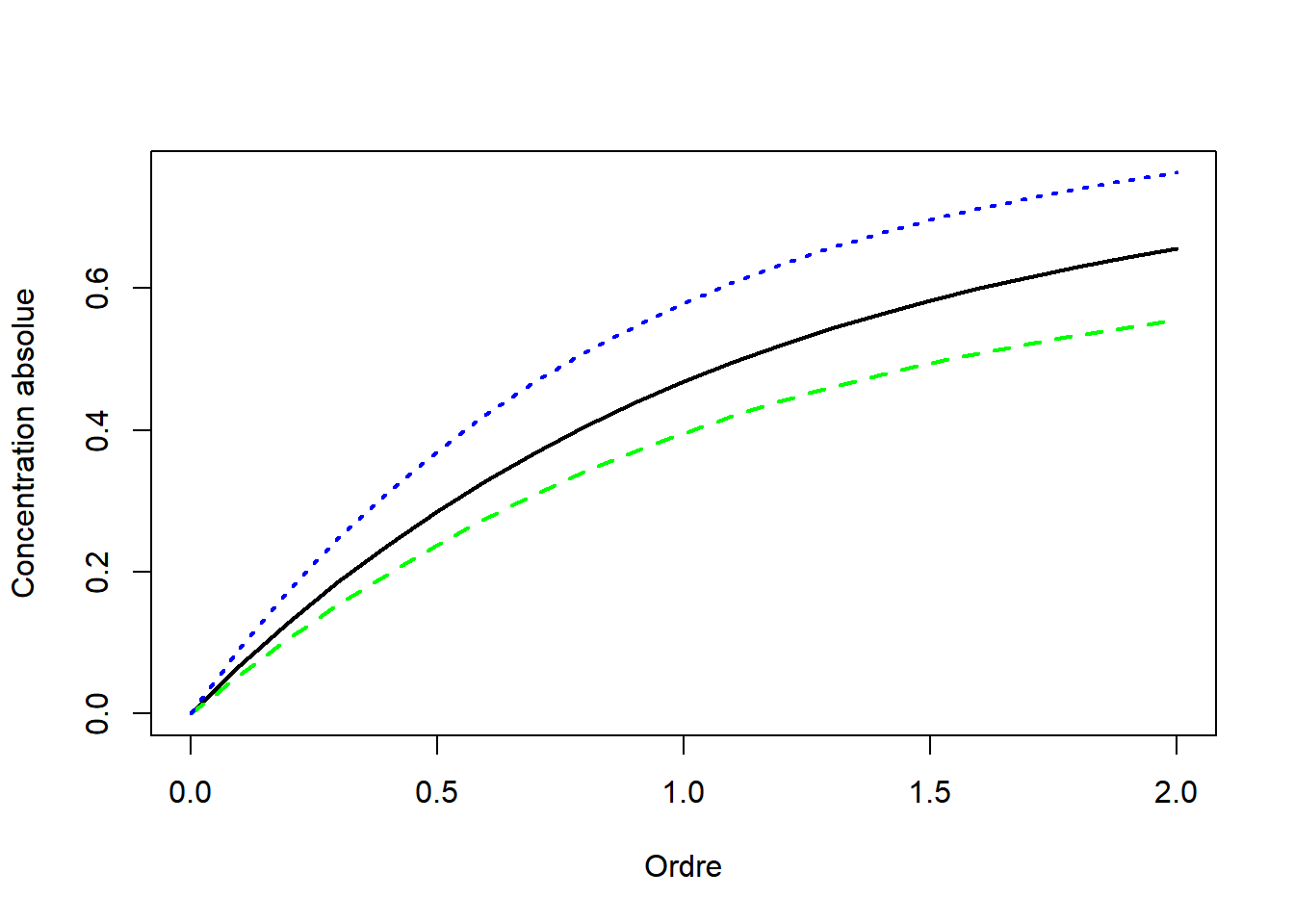
Figure 3.2: Profils de concentration absolue de l’industrie (courbe pleine, noire), du secteur C10 (pointillés longs, verts) et du secteur C20 (pointillés courts, bleus).
La valeur de la concentration est la proportion des pays délaissés (en nombres effectifs). Une valeur de 0 signifie que tous les pays sont occupés, une valeur de 1 que tout le secteur est concentré dans un seul pays. L’industrie chimique, C20, est beaucoup plus concentrée que l’industrie en général, alors que l’industrie agro-alimentaire, C10, l’est nettement moins. Ces résultats sont valides à tous les ordres, sauf près de 0, lorsque la présence seule du secteur compte, quel que soit son abondance.
Cette mesure de l’ubiquité ou de la concentration est absolue (Brülhart et Traeger 2005): elle ne compare le nombre effectif de secteurs à aucune référence externe. Pour son interprétation, une comparaison à une autre mesure absolue (la concentration à un niveau plus agrégé) est nécessaire (Marcon et Puech 2017)
3.1.2 Concentration relative
L’ubiquité absolue a été calculée au niveau des secteurs désagrégés (C10 et C20) et au niveau de l’industrie entière, dont les effectifs ont été obtenus par agrégation des ceux des secteurs. En reprenant la terminologie de la décomposition de la biodiversité, l’ubiquité absolue de l’industrie entière est l’ubiquité \(\gamma\), égale au produit de l’ubiquité \(\alpha\) (la moyenne des de celle des secteurs désagrégés) par l’ubiquité \(\beta\), nombre effectif de secteurs équiprobables, ne partageant aucun pays.
La décomposition de l’entropie est la même, mais l’entropie \(\gamma\) est la somme des entropies \(\alpha\) et \(\beta\). L’entropie \(\beta\) est, comme on l’a vu, la divergence de Jensen-Shannon généralisée entre la distribution de chaque secteur et la distribution agrégée de l’industrie. Aux ordres particuliers \(q=1\) et \(q=2\), cette divergence est la moyenne, pondérée par les poids des secteurs, de l’entropie relative de Theil et de la statistique \(G_s\) d’Ellison et Glaeser. Ces indices classiques de concentration spatiale sont des divergences de Kullback-Leibler généralisées, en d’autres termes des entropies \(\beta\) d’ordres particuliers, donnant une importance différente aux pays à faibles effectifs: l’indice d’Ellison et Glaeser, d’ordre 2, ne prend en compte que les implantations dominantes.
L’entropie \(\beta\) mesure la concentration relative: elle intègre une référence (la distribution de l’industrie tous secteurs confondus) et a donc une valeur attendue, 0, si la distribution de l’industrie considérée est identique à celle de référence.
Sa valeur n’est pas interprétable intuitivement: il faut recourir à l’ubiquité \(\beta\), nombre effectif de secteurs dont l’interprétation est claire. Dans le cadre de la décomposition présenté plus haut, l’ubiquité \(\beta\), concentration relative moyenne, est le rapport de l’ubiquité \(\gamma\) sur l’ubiquité \(\alpha\): elle s’applique à l’ensemble des secteurs mais ne donne pas d’information sur un secteur particulier. Elle doit donc être détaillée pour chaque secteur : la concentration relative du secteur \(s\) est définie comme le rapport entre l’ubiquité absolue de l’ensemble de l’industrie (\(\gamma\)) et son ubiquité absolue propre: \[^{q}C_{s} = ^{q}D(\mathbf{p_{i}}) / ^{q}D(\mathbf{p_{i|s}}).\]
C’est un nombre effectif de secteurs: si tous les secteurs avaient une ubiquité égale au nombre effectif de pays \(^{q}D(\mathbf{p_{i|s}})\), il en faudrait \(^{q}C_{s}\) pour obtenir une industrie dont l’ubiquité serait \(^{q}D(\mathbf{p_{i}})\) pays effectifs.
La valeur de la concentration relative est visible sur la figure 3.1: elle est égale au rapport entre les valeurs des profils d’ubiquité de l’industrie et du secteur considéré. Pour l’industrie chimique (C20), elle varie de 1 (à l’ordre 0) à 1.4 à l’ordre 2: 1.4 secteurs effectifs d’ubiquité effective celle du secteur C20, soit 6.7 pays, formeraient une industrie dont l’ubiquité serait celle observée pour l’industrie européenne, \(6.7 \times 1.4 = 9.3\) pays effectifs.
La concentration est inférieure à 1 pour l’industrie agro-alimentaire (C20): 0.79 secteurs effectifs de même caractéristiques que le secteur C10 suffiraient pour constituer l’ubiquité de l’industrie européenne. En d’autres termes, le secteur C10 est relativement dispersé.
La concentration relative et l’ubiquité absolue (figure 3.1) sont liées : leur produit est la concentration absolue de l’ensemble des secteurs, prise comme référence. La concentration absolue (figure 3.2) va donc de pair avec la concentration relative, mais les informations qu’elles fournissent sont différentes.
Dans la littérature économique, l’entropie relative a été utilisée pour mesurer la concentration relative par Brülhart et Traeger (2005). Mori, Nishikimi, et Smith (2005) ont utilisé la divergence de Kullback-Leibler entre la distribution d’un secteur et celle de la surface (au lieu du nombre de personnes travaillant dans l’industrie) des régions du Japon pour mesurer la concentration topographique (et non relative) des secteurs. Rysman et Greenstein (2005) ont proposé un test de la concentration relative d’un secteur fondé sur le rapport de vraisemblance des distributions du secteur et de l’industrie entière, qui est simplement la divergence de Kullback-Leibler (voir Mori, Nishikimi, et Smith 2005 pour une présentation détaillée des liens entre les deux approches). Alonso-Villar et Del Río (2013) ont proposé une décomposition de l’entropie généralisée mais se sont limités en pratique à l’ordre 1.
L’entropie relative de Theil a été utilisée pour comparer l’évolution de la concentration spatiale dans le temps (par exemple, Cutrini 2010) puisqu’elle obéit bien à une relation d’ordre comme toute entropie. Enfin, Bickenbach, Bode, et Krieger-Boden (2013) ont combiné l’indice de Theil (absolu) et l’indice relatif de Theil pour mieux décrire la concentration spatiale en les appliquant à des secteurs économiques différents (industrie et services).
3.2 Spécialisation
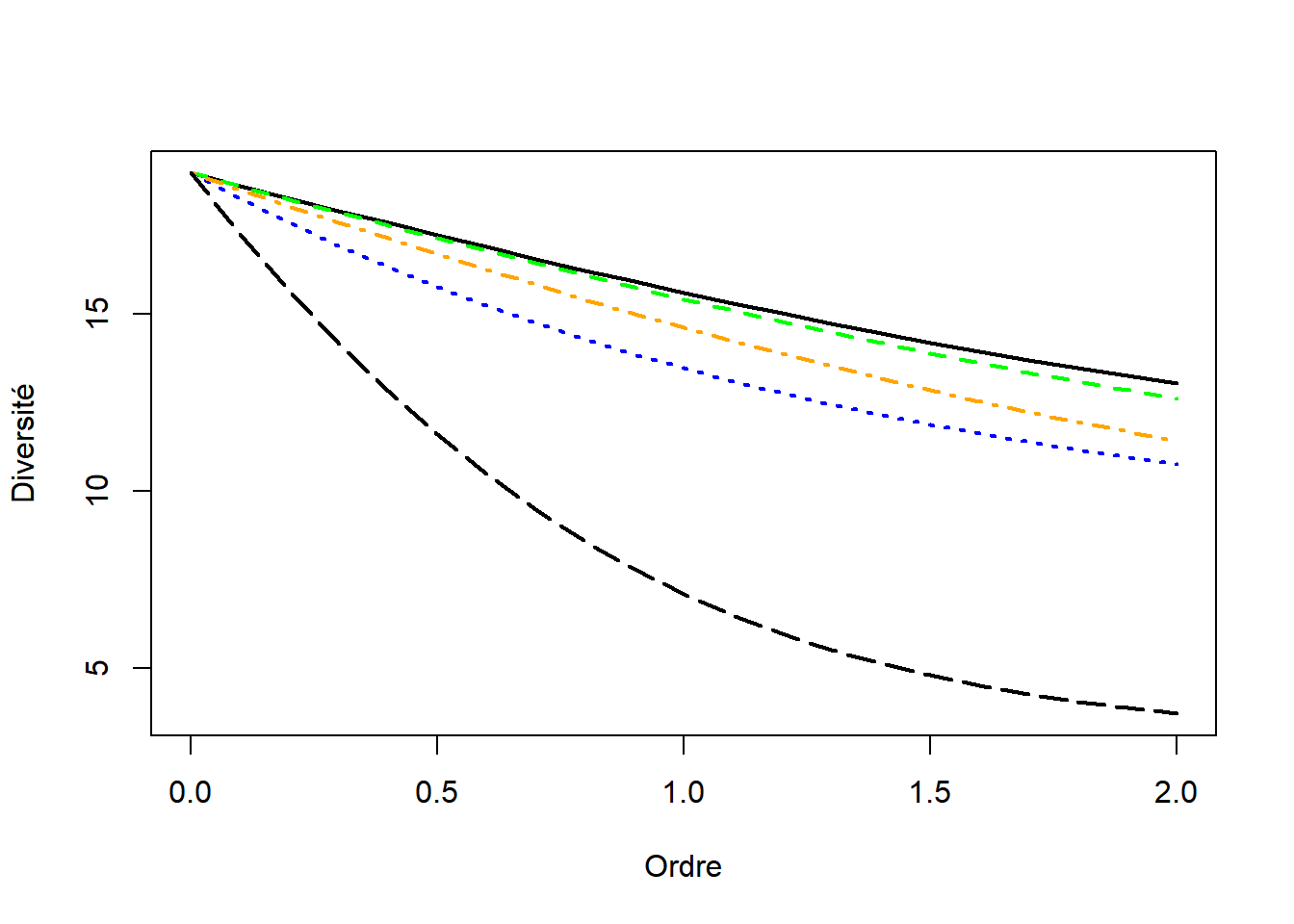
Figure 3.3: Profils de diversité de l’Europe (courbe pleine, noire), de l’Italie (pointillés longs, verts), de la France (pointillés alternés, orange), de l’Allemagne (pointillés courts, bleus) et de l’Islande (pointillés très longs, noirs).
La mesure de la spécialisation fonctionne exactement de la même manière que celle de la concentration, en échangeant le rôle des lignes et des colonnes du tableau de contingence.
La figure 3.3 présente les profils de diversité absolue de l’Italie, l’Allemagne, la France et l’Islande et de l’Europe. La diversité est le nombre effectif de secteurs équiprobables qui fourniraient la même diversité que celle observée. Comme précédemment, le niveau d’agrégation des données est tel que tous les secteurs sont représentés dans tous les pays : la richesse, c’est-à-dire la diversité d’ordre 0 est égale au nombre secteurs. Tous les pays sont moins divers que l’Europe : ils sont donc tous spécialisés à des degrés divers. L’Italie l’est assez peu, l’Allemagne l’est plus que la France et l’Islande est le pays le plus spécialisé d’Europe avec moins de 5 secteurs industriels effectifs à l’ordre 2, trois fois moins que l’Italie. L’agro-alimentaire, C10, emploie près de la moitié des personnes travaillant dans l’industrie en Islande.
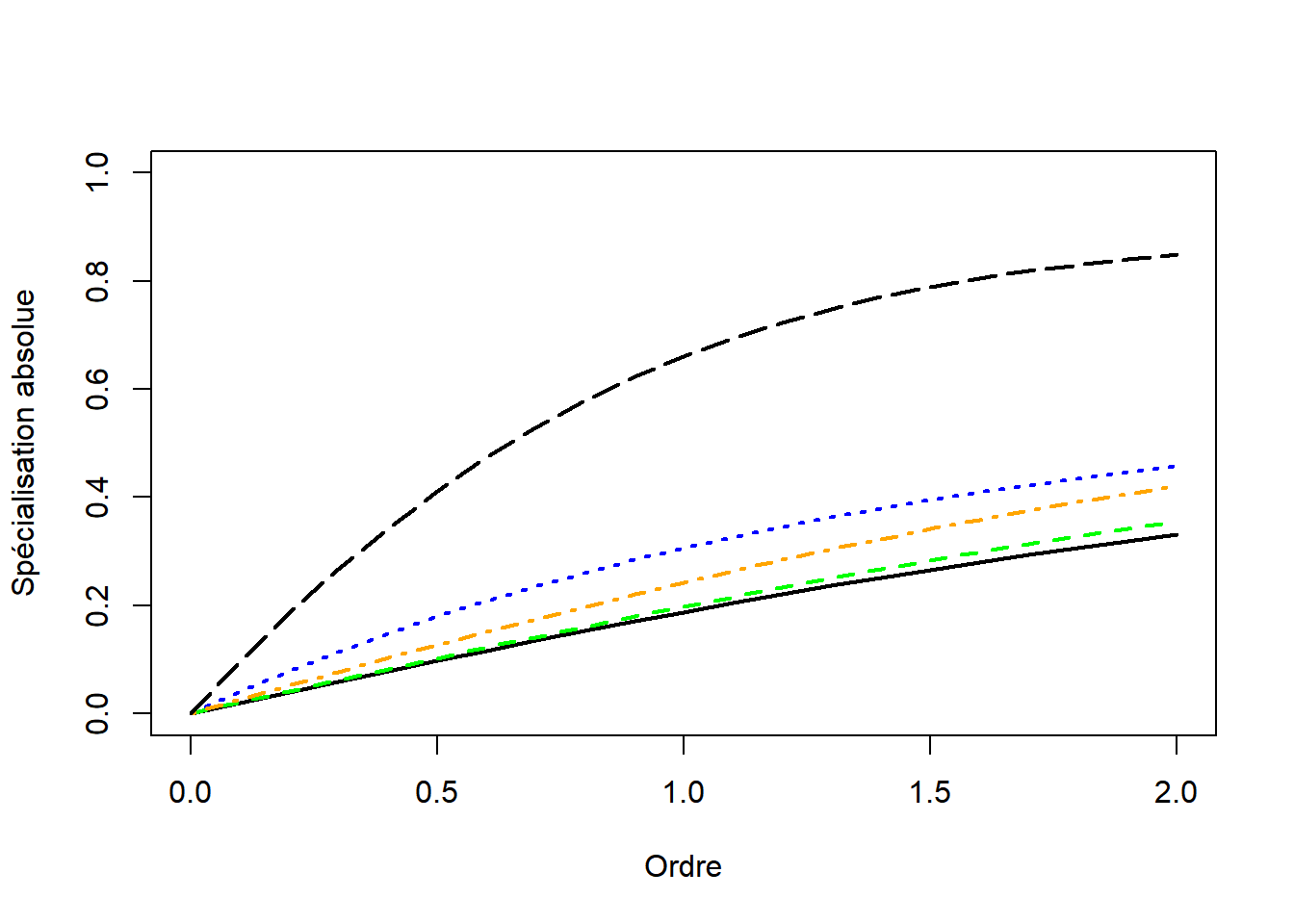
Figure 3.4: Profils de spécialisation absolue de l’Europe (courbe pleine, noire), de l’Italie (pointillés longs, verts), de la France (pointillés alternés, orange), de l’Allemagne (pointillés courts, bleus) et de l’Islande (pointillés très longs, noirs).
La diversité peut être transformée en spécialisation absolue, comme l’ubiquité l’a été en concentration, pour obtenir la figure 3.4.
Enfin, la spécialisation relative est le rapport entre la diversité absolue de l’Europe entière et celle de chaque pays, visible sur la figure 3.3. L’Islande est le pays le plus spécialisé relativement, avec une valeur à l’ordre 2 de 3.5 pays effectifs.
3.3 Tests de significativité
Deux approches sont envisageables pour tester les profils de concentration ou spécialisation. Pour fixer les idées et sans perte de généralité, il s’agit ici de tester la spécialisation de l’Italie contre l’hypothèse nulle qu’elle ne serait pas différente de celle de l’Europe entière.
La première formalisation de l’hypothèse nulle est que la distribution des secteurs industriels en Italie est la même que celle de l’Europe entière. Le test porte alors sur la valeur de la divergence de Kullback-Leibler généralisée entre la distribution des secteurs en Italie et la distribution des secteurs agrégée au niveau européen. C’est l’approche, pour la concentration spatiale, d’Ellison et Glaeser: \(G_s\) est la divergence d’ordre 2 entre la distribution du secteur \(s\) et celle de l’ensemble de l’industrie. C’est aussi celle de Mori, Nishikimi, et Smith (2005) à l’ordre 1. Elle soufre de la non-indépendance des entropies \(\alpha\) et \(\beta\) (Jost 2007): la statistique testée est l’entropie \(\beta\) mais sa valeur est contrainte par celles de l’entropie \(\alpha\) pour une valeur donnée (de référence) de l’entropie \(\gamma\). Une illustration du problème est qu’à l’ordre 0 l’entropie \(\beta\) est significativement différente de 0 alors que tous les secteurs sont présents en Italie.
La formalisation alternative est que la spécialisation de l’Italie est égale à celle d’un pays de même taille dont la distribution des secteurs serait celle de l’Europe entière. La statistique testée est un nombre effectif (la diversité absolue ou la spécialisation relative, de façon équivalente). C’est l’approche retenue ici.
Le test est réalisé en générant aléatoirement, un grand nombre de fois, de nouvelles données correspondant à l’hypothèse nulle, en calculant la statistique d’intérêt. Les données sont simulées par 1000 tirages dans une loi multinomiale dont les paramètres sont le nombre de personnes travaillant en Italie et les probabilités des secteurs au niveau européen. La spécialisation de chaque simulation est calculée pour les ordres de 0 à 2, par intervalles de \(0.1\). Les quantiles correspondant à 2.5% et 97.5% des spécialisation simulées constituent les limites de l’enveloppe de confiance de la statistique sous l’hypothèse nulle, à laquelle est comparée la spécialisation réelle.
Le détail du test est présenté en annexe. L’hypothèse nulle est acceptée à l’ordre 0: la spécialisation de l’Italie est identique à celle de l’Europe puisque dans les deux cas tous les secteurs sont présents. Dès l’ordre \(0.1\), l’hypothèse nulle est rejetée : l’Italie est plus spécialisée que l’Europe.
La variabilité de la spécialisation simulée est extrêmement faible parce que les effectifs sont grands et que les personnes sont redistribuées indépendamment les unes des autres par la loi multinomiale. Pour cette raison, Mori, Nishikimi, et Smith (2005), à partir de données similaires, choisit de tester la concentration spatiale des établissement en ignorant leurs effectifs. Une bien meilleure hypothèse nulle est que les établissement sont distribués aléatoirement, mais avec leur taille réelle, ce qui augmente fortement l’incertitude sur la spécialisation simulée. Des données individuelles sur les établissement, ou au minimum sur la distribution de leurs tailles, sont nécessaires pour aller plus loin. Avec les données disponibles, tous les profils présentés dans les figures 3.1 à 3.4 sont significativement différents les uns des autres dès l’ordre \(0.1\).