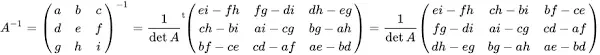
Theory

Inversion of large matrices is difficult. Newman (1974) proposes a method for testing inversion accuracy.

Let \(A\) be the (square, non-singular) matrix to be inverted. \(X\) is the approximation of \(A^{-1}\) obtained by calculation. \(N(Y)={sqrt{sum_{i,j}{y_{i,j}^2}}\) is the Euclidean norm of a matrix \(Y=(y_{i,j})\).

\(R = I - AX\) is the difference (ideally zero) between the identity matrix and the product of \(A\) and its calculated inverse.

The norm of \(R\) is not a good indicator of inversion accuracy (Newman, 1974, section 3). On the other hand, the norm of \(A^{-1} - X\) is, but \(A^{-1}\) is unknown. Newman shows that \[\frac{N(XR)}{1 + N(XR)} \leq N(A^{-1} - X) \leq \frac{N(XR)}{1 - N(XR)},\] which allows to bound the value of \(N(A^{-1} - X)\) between the calculated values of \(X\) and \(R\).

The aim is for this value to be small, ideally zero if \(A^{-1} = X\), relative to the norm of \(X\).

Example

The size parameter sets the size (number of rows and columns) of the matrices used, here a 1000 x 1000 matrix.

size <- 1000

A matrix is created:

A <- matrix(rnorm(size^2), nrow = size)

It is inverted numerically (\(X\) is calculated), then \(R\) and \(XR\) are calculated:

X <- solve(A)
AX <- A %*% X
R <- diag(size) - AX
XR <- X %*% R

The Euclidean norm function is defined:

norm.matrix <- function(X) {
  sqrt(sum(X^2))
}

Matrix norms are calculated:

# Matrix to invert
norm.matrix(A)

## [1] 998.9248

# Numerical inversion
norm.matrix(X)

## [1] 42.73308

# Inversion deviation
norm_R <- norm.matrix(R)
norm_XR <- norm.matrix(XR)

Finally, the bounds of the norm of \(A^{-1} - X\) is provided:

norm_XR / (1 + norm_R)

## [1] 8.102206e-12

norm_XR / (1 - norm_R)

## [1] 8.102206e-12

The norm of \(A^{-1} - X\) is very close to 0: matrix inversion in R works well.

Reference

Newman, M. (1974). How to Determine the Accuracy of the Output of a Matrix Inversion Program. JOURNAL OF RESEARCH of the National Bureau of Standards - B. Mathematical Sciences, 788(2), 65–68.