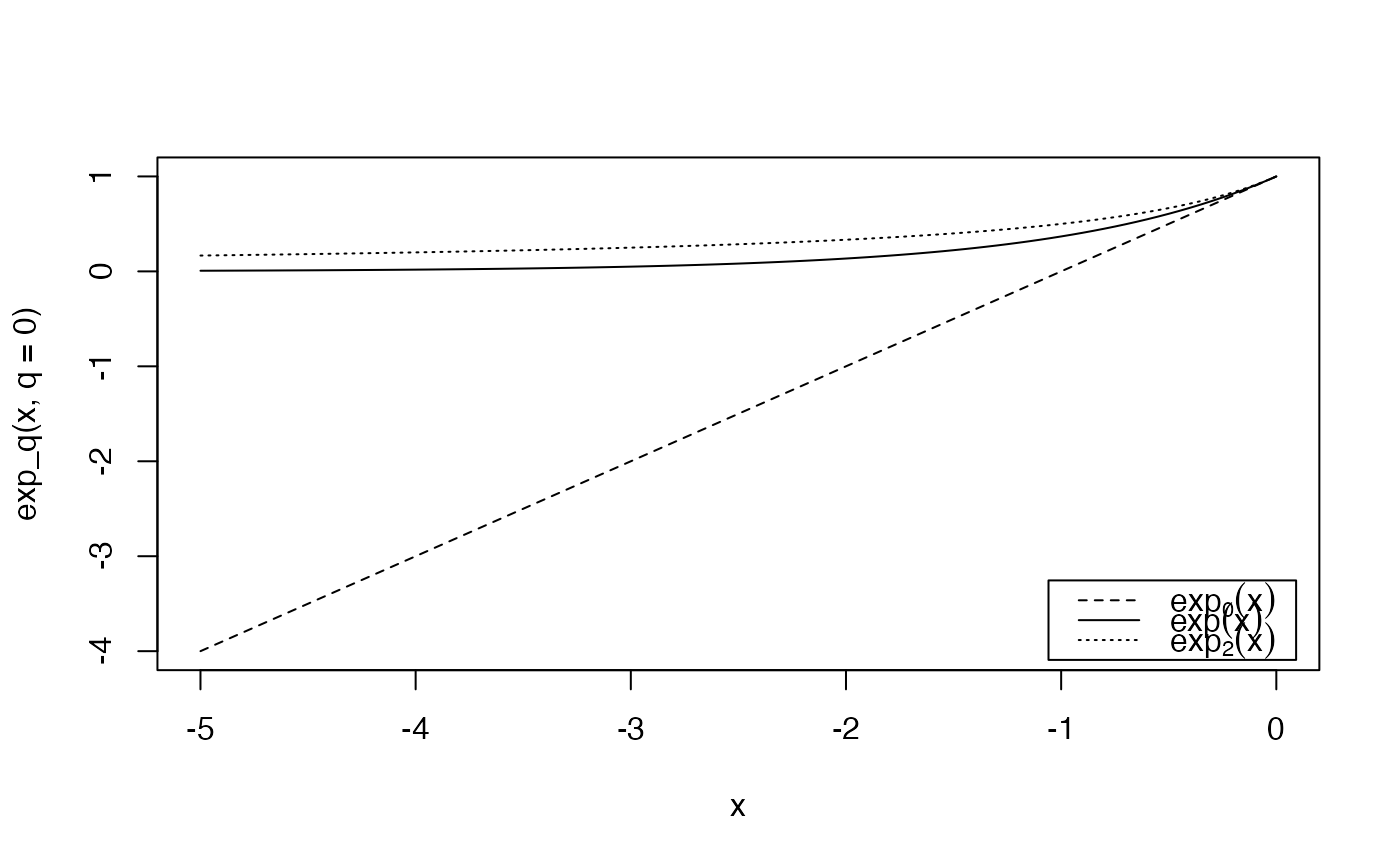
Calculate the deformed exponential of order q.
Details
The deformed exponential is the reciprocal of the deformed logarithm (Tsallis 1994) , see ln_q. It is defined as \((x(1-q)+1)^{\frac{1}{(1-q)}}\).
For \(q>1\), \(\ln_q{(+\infty)}=\frac{1}{(q-1)}\)
so \(\exp_q{(x)}\) is not defined for \(x>\frac{1}{(q-1)}\).
When x is very close to this value, the exponential is severely subject
to rounding errors.
References
Tsallis C (1994). “What Are the Numbers That Experiments Provide?” Química Nova, 17(6), 468–471.
Examples
curve(exp_q(x, q = 0), from = -5, to = 0, lty = 2)
curve(exp(x), from = -5, to = 0, lty= 1, add = TRUE)
curve(exp_q(x, q = 2), from = -5, to = 0, lty = 3, add = TRUE)
legend("bottomright",
legend = c(
expression(exp[0](x)),
expression(exp(x)),
expression(exp[2](x))
),
lty = c(2, 1, 3),
inset = 0.02
)