1 Processus classiques

Les processus ponctuels fournissent le cadre mathématique nécessaire à l’étude des structures spatiales. Une définition mathématique est nécessaire avant de présenter les processus les plus courants, dont le processus de Poisson. L’approche utilisée classiquement par les non-mathématiciens est locale : les propriétés d’un processus sont définies autour de chaque point. Elle a l’avantage d’être concrète et facilement compréhensible. Son inconvénient est de laisser un certain flou sur le comportement global du processus. Une définition globale est nécessaire pour aller plus loin : c’est celle que nous présenterons en première partie de ce chapitre. La définition locale est présentée en-suite pour les lecteurs rebutés par les équations.

Ensuite, nous analyserons en détail quelques processus classiques, choisis pour leur utilité en écologie puis les méthodes nécessaires à leur simulation.

1.1 Définitions

1.1.1 Processus ponctuel

Nous nous placerons dans une partie du plan, typiquement une placette forestière, notée \(A\), \(A \subset R^2\). Les définitions données ici et la plupart des résultats sont valables dans un espace de dimension quelconque finie mais on se limitera en pratique à un espace à deux dimensions. D’autre part, travailler sur une placette de taille infinie n’a pas d’intérêt pratique, mais rien ne s’y opposerait sur le plan mathématique, sauf dans certains cas qui seront précisés dans le texte. \(A\) sera appelée aire ou zone ou fenêtre d’étude.

Nous nous intéresserons à des ensembles dénombrables de points (on dira aussi “semis de points”). Les points seront notés en minuscules, les ensembles en majuscules : \(X \subset R^2\) , \(x \in X\). Le semis de point \(X\) sera généralement défini sur tout le plan, et son nombre de points sera infini. À l’intérieur de l’aire d’étude \(A\), un sous ensemble de \(X\) noté \(X_A\) sera observé et cartographié : \(X_A = X \cap A\).

Nous ne nous intéresserons qu’à des ensembles de points localement finis, c’est-à-dire tels que leur nombre de points dans \(A\) soit fini : \(n(A) < \infty\) pour \(A\) borné. Cette restriction n’a pas de conséquences pratiques.

Il est impossible de définir directement une fonction qui attribuerait à chaque semis la probabilité de le tirer, parce que la probabilité de chaque semis est nulle. On passe donc par des ensembles de semis de points, dont la probabilité n’est pas nulle. L’ensemble des semis de points localement finis est noté \(N_f\). \(N_f\) peut être équipé d’une \(\sigma\)-algèbre \(\mathcal{N_f}\). Les éléments \(F\) de \(\mathcal{N_f}\) sont des ensembles de semis de points localement finis. \(\mathcal{N_f}\) est une tribu (ou \(\sigma\)-algèbre) de \(N_f\) :

• l’ensemble vide appartient à \(\mathcal{N_f}\);

• pour tout \(F \in \mathcal{N_f}\), le complémentaire de \(F\) dans \(\mathcal{N_f}\) appartient aussi à \(\mathcal{N_f}\);

• l’union de \((F_1, F_2, F_3,…)\), une suite dénombrable d’éléments de \(\mathcal{N_f}\) appartient aussi à \(\mathcal{N_f}\).

\((N_f, \mathcal{N_f})\) est un espace probabilisable. Il reste à le doter d’une mesure \(P\), la probabilité de tirer un ensemble de semis de points particulier \(F\). Cet ensemble est défini par le nombre de points tirés, \(N(A)\), pour tout \(A\) borné. \(P\) est une mesure car :

• \(P(\emptyset)=0\)

• \(P\) est \(\sigma\)-additive : \(P(\bigcup_{i=1}^n F_i) = \sum_{i=1}^n {P(F_i)}\), où \(\bigcup_(i=1)^n F_i\) est une union disjointe.

\(P\) est une probabilité car on fixe \(P(\mathcal{N_f})=1\).

Un processus ponctuel est défini comme une application d’un espace de probabilité \((\Omega, \mathcal{F}, \mathcal{P})\) vers \((N_f,\mathcal{N_f})\) tel que \(N(A)\) est une variable aléatoire pour tout \(A\) borné. La définition précise de \((\Omega, F, P)\) importe peu puisqu’il est impossible à utiliser directement. Les processus sont notés en lettres grecques majuscules, par exemple \(\Xi\). Un semis de points \(X\) est une réalisation de \(Xi\). On note \(P(X \in F)\) la probabilité que le tirage de \(\Xi\) soit un élément d’un ensemble de semis de points \(F\) particulier, par exemple défini par son nombre de points. Enfin, la surface de A sera notée \(\|A\|\).

1.1.2 Propriété de premier ordre

Soit \(S\) une partie de \(A\). La propriété de premier ordre \(\mu(S)\), appelée également mesure d’intensité du processus \(\Xi\), est l’espérance du nombre de points dans \(S\) :

\[\begin{equation} \mu(S)=\mathop{\mathbb{E}}(N(S)) \tag{1.1} \end{equation}\] Dans tous les cas que nous traiterons, la mesure d’intensité pourra être écrite comme l’intégrale d’une fonction d’intensité \(\lambda\) : \[\begin{equation} \mu(S)=\int_S{\lambda(x)dx} \tag{1.2} \end{equation}\]

1.1.3 Propriété de second ordre

La mesure du moment factoriel de second ordre de deux parties de \(A\), \(S_1\) et \(S_2\), est l’espérance du nombre de paires de points du processus \(\Xi\) se trouvant respectivement dans \(S_1\) et \(S_2\) :

\[\begin{equation} \mu_2(S_1,S_2 ) = \mathop{\mathbb{E}}\left(\sum_{x_1 ,x_2 \in X, x_1 \ne x_2}{1(x_1 \in S_1, x_2 \in S_2)} \right) \tag{1.3} \end{equation}\] De même, cette mesure pourra être écrite comme l’intégrale de \(\lambda_2\), appelée densité du produit de second ordre : \[\begin{equation} \mu_2 S_1,S_2 ) = \iint_{(R^2)^2}{1(x_1 \in S_1, x_2 \in S_2) \lambda_2(x_1, x_2)dx_1 dx_2} \end{equation}\]

On peut montrer (Møller et Waagepetersen 2004) que : \[ \mathop{\mathbb{E}}(N(S_1 )N(S_2 )) = \lambda_2(S_1,S_2)+\lambda(S_1 \cap S_2)\]

1.2 Définition locale

Un processus ponctuel est l’équivalent d’une variable aléatoire dont le résultat est un ensemble de points noté \(X\), dans un ensemble de réalisations possibles, qui sera toujours ici une surface connue et délimitée notée \(A\).

On utilise les processus ponctuels comme outils mathématiques pour caractériser et éventuellement modéliser des événements dont on connaît la répartition spatiale, par exemple les arbres dans une forêt. Une façon intéressante de décrire un processus ponctuel dont on ne connaît pas la loi consiste à utiliser ses propriétés de premier ordre et de second ordre.

1.3 Processus de Poisson homogène

Le processus de Poisson est un processus stationnaire et isotrope, dont la réalisation donne des points à la position complètement aléatoire. Inversement, un processus ponctuel complètement aléatoire est un processus de Poisson (démonstration : Diggle 1983, pp. 51-52).

Le processus de Poisson joue un rôle central en statistiques spatiales, à la fois parce que c’est le plus simple donc celui dont les propriétés ont été le mieux étudiées, et aussi parce qu’il constitue généralement le modèle nul contre lequel des semis de points peuvent être testés. C’est un processus à accroissements indépendants, il joue le rôle des marches aléatoires pour les séries temporelles à temps discret et du mouvement Brownien pour les séries à temps continu. Ces propriétés sont utilisées pour le calcul de l’intervalle de confiance de la fonction K de Ripley.

1.3.1 Simulation

La simulation d’un processus de Poisson (figure 1.1) est faite par la commande rpoispp de spatstat.

X <-rpoispp(lambda=1, win=as.owin(c(0, 10, 0, 10)))
plot(X, main="")
axis(1); axis(2)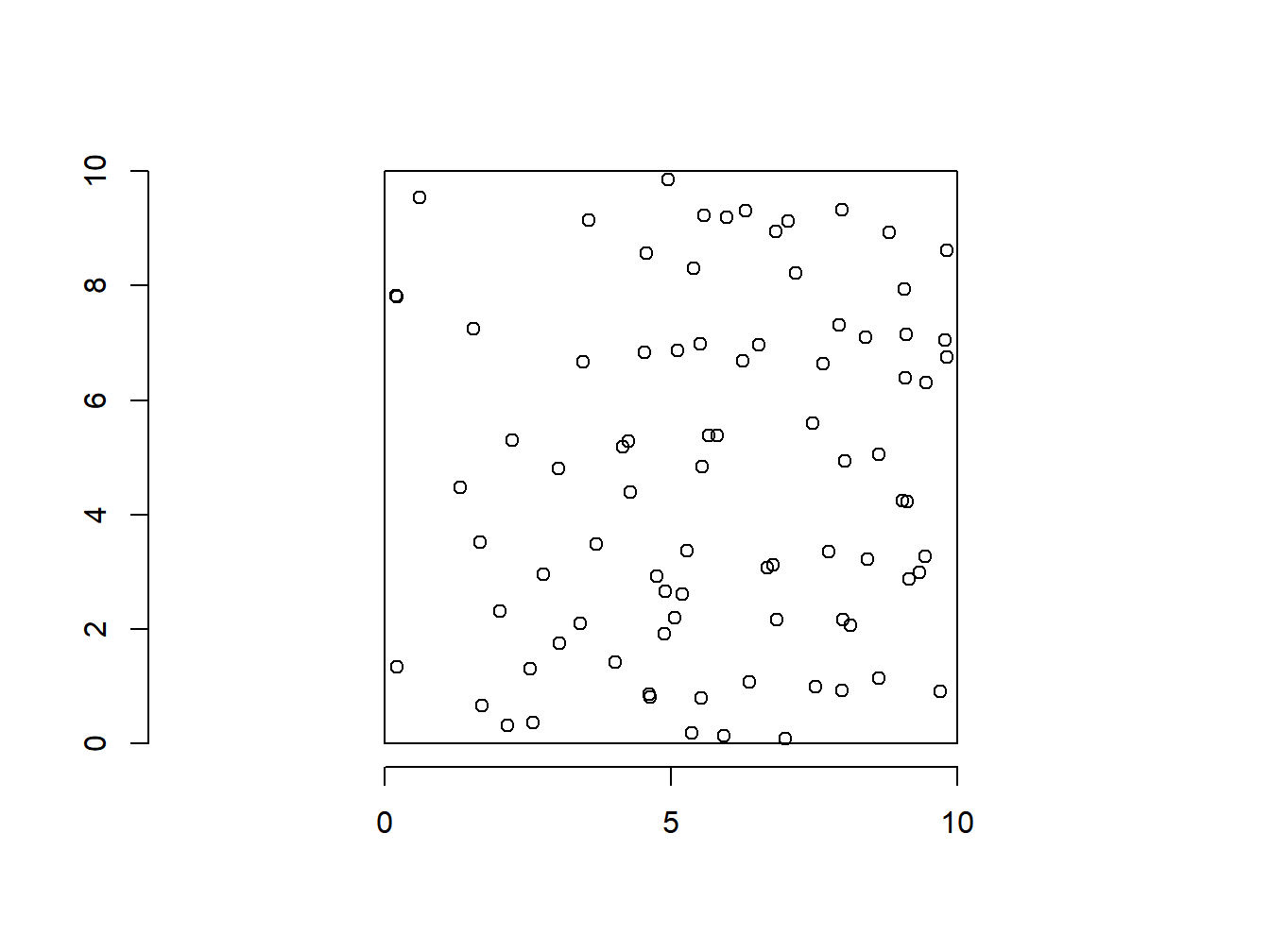

Figure 1.1: Simulation d’un processus de Poisson homogène d’intensité 1

Les arguments de la fonction sont l’intensité du processus \(\lambda\) (cf. Propriété de premier ordre) et la fenêtre \(A\), ici un carré dont les coordonnées des sommets sont listées.

1.3.2 Propriété de premier ordre

Une réalisation d’un processus de Poisson de paramètre \(\lambda A\) sur l’aire d’étude A est un semis de points complètement aléatoire d’intensité \(\lambda\). Le nombre de points suit une loi de Poisson de paramètre \(\lambda A\), c’est-à-dire que :

\[\begin{equation} P(n(A)=k) = e^{-\lambda A} \frac{(\lambda A)^k}{k!}. \tag{1.4} \end{equation}\]

References

Møller, Jesper, et Rasmus Plenge Waagepetersen. 2004. Statistical Inference and Simulation for Spatial Point Processes. Vol. 100. Chapman; Hall.

Diggle, Peter J. 1983. Statistical analysis of spatial point patterns. London: Academic Press.