Logarithm of order q

Calculates the deformed logarithm of order \(q\).

Usage

lnq(x, q)
lnq.CommunityProfile(Profile)

Arguments

x

A numeric vector.

Profile

A CommunityProfile.

q

A number.

Details

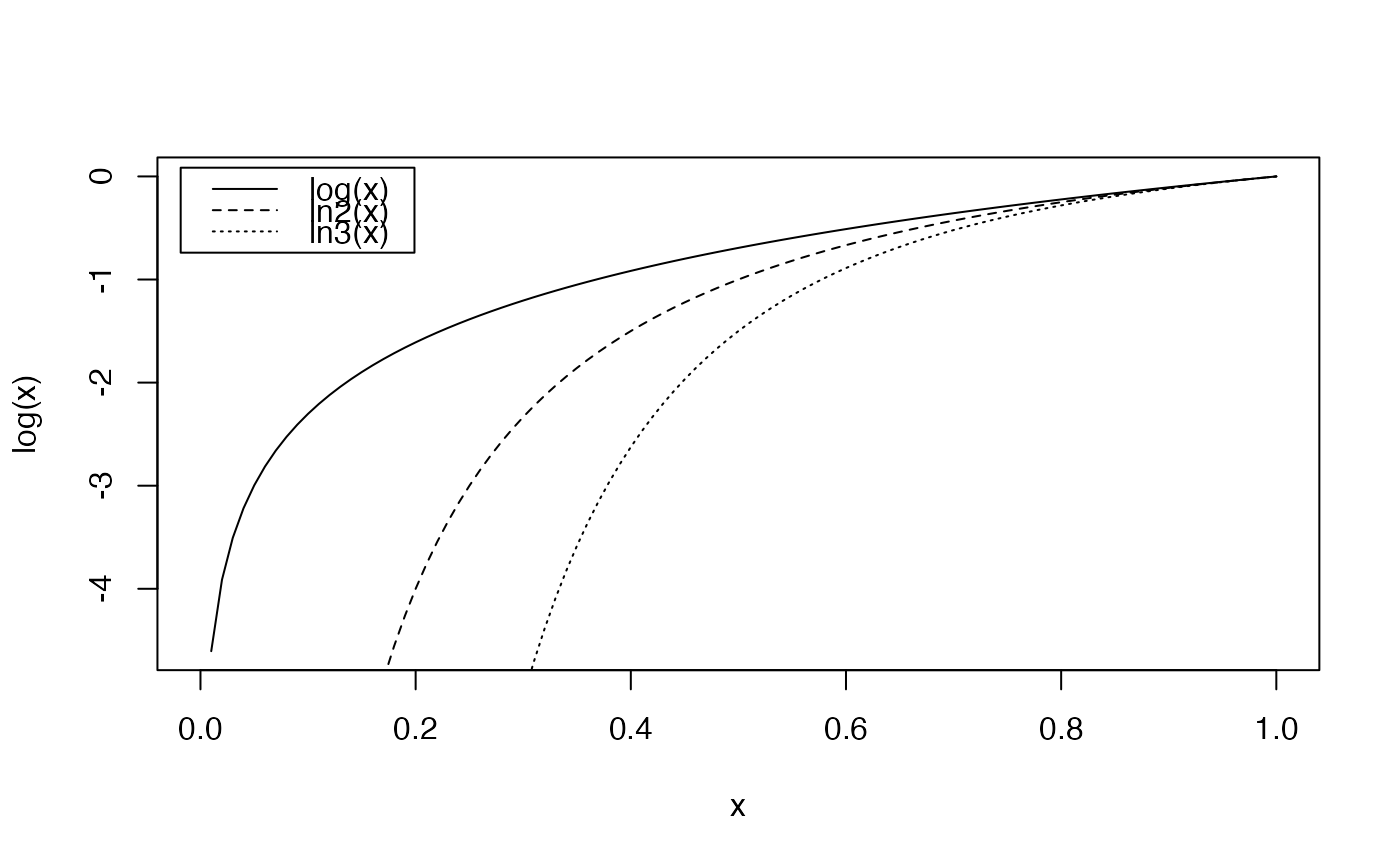
The deformed logarithm is defined as \(\ln_q{x}=\frac{(x^{(1-q)}-1)}{(1-q)}\).

The shape of the deformed logarithm is similar to that of the regular one. \(\ln_1{x}=\log{x}\).

For \(q>1\), \(\ln_q{(+\infty)}=\frac{1}{(q-1)}\).

lnq.CommunityProfile calculates the deformed logarithm of a CommunityProfile. Its $x item (the order of diversity) is kept unchanged whilst other items are set to their logarithm of order $x. Thus, a diversity profile is transformed into an entropy profile.

Value

A vector of the same length as x containing the transformed values or a CommunityProfile.

References

Tsallis, C. (1994). What are the numbers that experiments provide? Quimica Nova 17(6): 468-471.

See also

expq

Examples

curve(log(x), 0, 1, lty=1)
curve(lnq(x, 2), 0, 1, lty=2, add=TRUE)
curve(lnq(x, 3), 0, 1, lty=3, add=TRUE)  
legend("topleft", legend = c("log(x)", "ln2(x)", "ln3(x)"), lty = c(1, 2, 3), inset=0.02)