22 Diversité régionale

La relation d’Arrhenius prévoit que logarithme du nombre d’espèces soit proportionnel au logarithme de la surface (de façon équivalente, que le nombre d’espèces soit proportionnel à la surface à une puissance \(z\) constante). Elle est plus robuste à l’échelle régionale que le modèle de Gleason qui prédit que le nombre d’espèces, plutôt que son logarithme, soit en relation linéaire avec le logarithme de la surface (très proche du modèle de Fisher dans lequel le nombre d’espèces est proportionnel au logarithme du nombre d’individus échantillonnés à partir d’une certaine surface).

En forêt tempérée, toutes les espèces d’un habitat sont rencontrées sur une surface inférieure à l’hectare. L’aire minimale est la surface nécessaire à échantillonner pour caractériser une association végétale, dans l’approche de la phytosociologie fondée par Braun-Blanquet (1928) et plus largement (Greig-Smith 1983), même si son intérêt est discuté (McGuinness 1984) : elle ne contient pas toutes les espèces mais un sous-ensemble caractéristique. Elle est de l’ordre de 200 m² en Europe (Chytrý et Otýpková 2003). L’augmentation de la surface intègre de nouveaux habitats et ajoute donc la diversité \(\beta\), par sauts successifs dans la situation idéale.

En forêt tropicale, il existe de nombreuses espèces rares, au sens où la probabilité de ne pas les rencontrer à l’occasion d’un échantillonnage d’une certaine taille n’est pas négligeable. L’expérience montre que l’augmentation de l’aire d’échantillonnage n’est pas la solution adaptée, puisqu’on rencontre toujours de nouvelles espèces (Gotelli et Colwell 2001), même en échantillonnant des surfaces considérables (50 ha pour la figure 22.3 au-delà du million de km² pour la figure 22.1). L’intégration de la diversité \(\beta\) due aux nouveaux habitats inventoriés se confond avec la progression de l’accumulation de la diversité locale. Dans le cas général, la SAR ne tend alors pas vers une asymptote, et nombre d’espèces augmente tant que la surface échantillonnée croît (Williamson, Gaston, et Lonsdale 2001). Il ne s’agit donc pas d’estimer un nombre d’espèces asymptotique pour une communauté, mais un nombre dépendant de la surface d’échantillonnage.

Une revue historique des théories sur la forme de la SAR est fournie par McGuinness (1984).

22.1 La relation d’Arrhenius

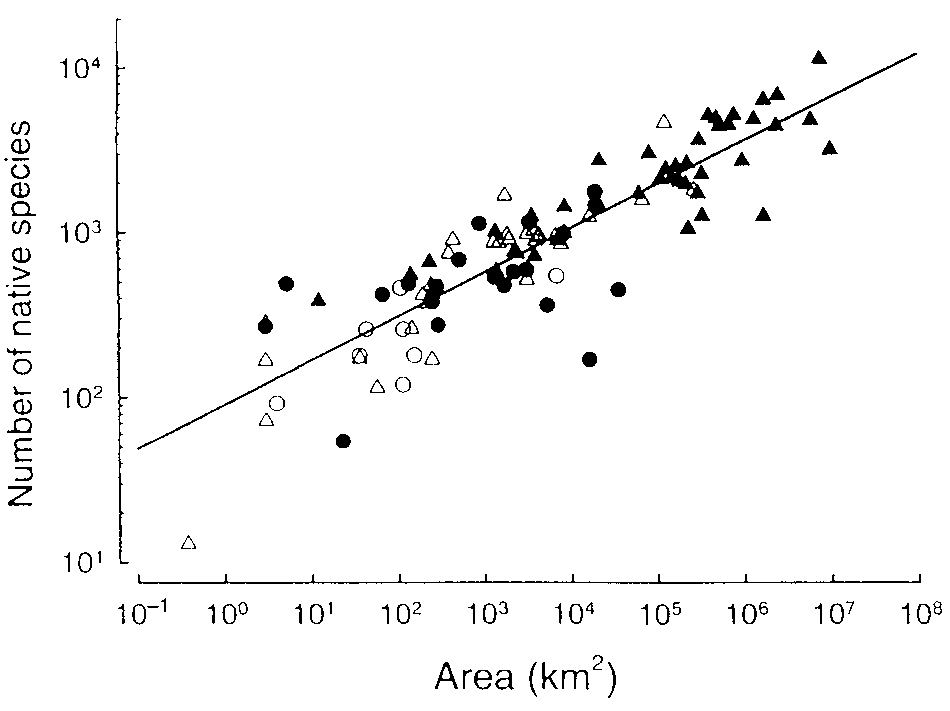
Figure 22.1: Logarithme du nombre d’espèces en fonction du logarithme de la surface échantillonnée. Les données sont des relevés d’espèces natives de plantes vasculaires sur 104 sites de taille variable à travers le monde. Les symboles correspondent à divers types d’habitats (îles ou continent, réserves ou non) sans intérêt ici. La valeur de \(z\) est 0,27.

22.1.1 Loi de puissance

Arrhenius (1921) a établi le modèle de base, dit loi de puissance :

\[\begin{equation} \tag{22.1} S^{A} = c A^{z}. \end{equation}\]

\(A\) est la surface, \(S^{A}\) est le nombre d’espèces dans \(A\), \(c\) et \(z\) des paramètres.

Preston (1962) a montré que si la distribution des espèces est log-normale (sur un ensemble d’îles), la SAR (le nombre d’espèces en fonction de la surface de chaque île, mais en aucun cas la SAC de chaque île) suit une loi de puissance, et a établi que la puissance \(z\) valait environ 0,26 (à partir de données empiriques, pas par nécessité théorique). On notera que le nombre d’espèces est clairement fini dans ce cadre, mais que la SAR n’a pas d’asymptote : les deux notions ne sont pas équivalentes. La loi de puissance peut donc être bornée. Le glissement d’un modèle de biogéographie des îles à un cadre plus général est faisable simplement, à la manière de Stephen P. Hubbell (2001) pour la théorie neutre : chaque île peut être considérée comme une communauté locale issue d’une méta-communauté régionale.

La distribution log-normale de Preston, dite “canonique” assumait une relation particulière entre le nombre d’espèces et le nombre d’individus, pour laquelle May (1975) a montré que la valeur exacte de \(z\) est 0,25. Les résultats empiriques ultérieurs (May 1975; May et Stumpf 2000), pour des lois quelconques, non canoniques, ont fourni des valeurs généralement comprises entre 0,2 et 0,3. Une large méta-analyse (Drakare, Lennon, et Hillebrand 2006) à partir de 794 SAR d’origine très différentes fournit une moyenne de 0,27, comme la méta-analyse de la figure 22.1 extraite de Williamson, Gaston, et Lonsdale (2001) à partir de données de Lonsdale (1999), mais avec une certaine variabilité que les auteurs relient à l’échelle spatiale, au type d’organismes et aux habitats échantillonnés, mais aussi à la technique d’échantillonnage.

Le paramètre le plus variable de la loi de puissance reste donc \(c\), un facteur d’échelle dépendant de la richesse de l’habitat.

Représentée en logarithmes, la relation est une droite (figure 22.1) :

\[\begin{equation} \tag{22.2} \ln S^{A} = \ln c + z\ln A. \end{equation}\]

La constante \(c\) est ignorée par la majorité de la littérature (Gould 1979) mais présente un intérêt pour la comparaison de courbes de même pente. La remarquable constance de la valeur de \(z\) est donc utile ici. Le rapport des valeurs de la constante pour deux régions par exemple permet de comparer leur richesse : à taille identique, les îles Philippines ont 6 fois plus d’espèces d’oiseaux que l’archipel de Hawaï (\(z=0,31\), \(c\) vaut respectivement 12 et 2). Sur un même territoire, le rapport entre le nombre d’espèces de deux taxons est le rapport des constantes si \(z\) est identique : par exemple, 1,5 espèces d’oiseaux par espèce de plante dans une partie de l’archipel d’Hawaï.

22.1.2 Le modèle de Plotkin

Plotkin, Potts, Yu, et al. (2000) ont eu accès à de grands échantillons (5 placettes de 50 hectares de forêt dans l’ensemble du monde tropical, figure 22.2, toutes déterminées correctement sur le plan botanique et dans lesquels chaque arbre est positionné). Ils montrent que le modèle d’Arrhenius comme les SAD classiques rendent mal compte de la réalité (figure 22.3a) quand on les compare aux courbes d’accumulation à l’échelle locale.

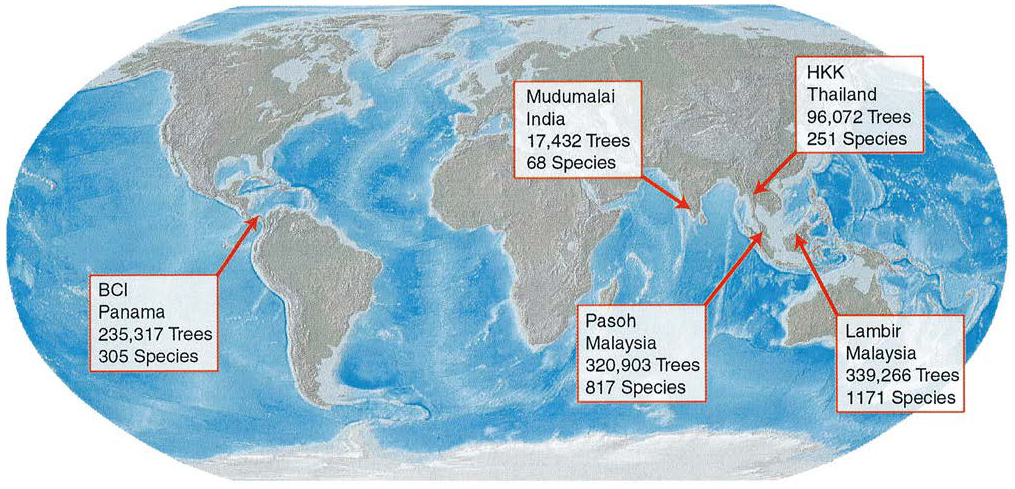
Figure 22.2: Les cinq dispositifs de Plotkin et al. Chaque dispositif mesure 50 ha et toutes les tiges de diamètre supérieur à 1 cm sont cartographiées et déterminées.

Harte, Kinzig, et Green (1999) ont montré que la loi de puissance était équivalente au modèle d’autosimilarité, dérivé de la théorie des fractales. On considère un rectangle \(A_i\) dont le rapport longueur sur largeur vaut \(\sqrt{2}\). On obtient le rectangle \(A_{i+1}\) en plaçant deux rectangles \(A_i\) côte à côte (et donc le rectangle \(A_{i-1}\) en coupant \(A_i\) en deux). \(\hat{S}^{A_i}\) est le nombre d’espèces rencontrées dans \(A_i\). On définit enfin \(a_i=\hat{S}^{A_{i-1}}/\hat{S}^{A_i}\) le facteur de diminution du nombre d’espèces (dit paramètre de persistance) lié à la division par 2 de la taille du rectangle.

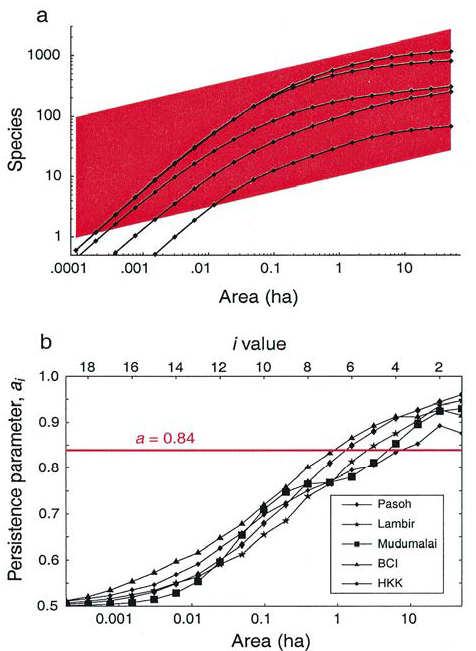
Figure 22.3: Courbes aire-espèces (a) et paramètre de persistance en fonction de la surface (b) dans 5 forêts tropicales. Le modèle d’Arrhenius est représentée par le parallélogramme sur la figure a, pour une gamme de valeurs de la constante. Elle implique que la relation aire-espèces représentée en logarithmes soit une droite, dont la position dépend de la constante, ce qui n’est visiblement pas le cas.

S’il s’agit d’une constante, \(a\), indépendante de la taille du rectangle, l’habitat est dit auto-similaire : l’augmentation du nombre d’espèces ne dépend pas de l’échelle d’observation Si cette condition est respectée, le nombre d’espèces suit la loi de puissance, et \(a=2^{-z}\). Pour la valeur classique de \(z=0,25\), \(a=0,84\). La figure 22.3b (Plotkin, Potts, Yu, et al. 2000) présente la valeur de \(a_i\) en fonction de la surface échantillonnée. Elle augmente avec la surface, ce qui infirme le modèle d’autosimilarité.

Plotkin, Potts, Yu, et al. (2000) ne supposent pas \(a_i\) constant et lui imposent simplement d’être une fonction de la surface, choisie arbitrairement pour permettre les calculs ultérieurs, et dont la forme correspond aux observations de la figure 22.3b. Après calculs, la relation aire-espèces est \(S^{A}\approx cA^z e^{-p\left(A\right)}\). \(p(A)\) est un polynôme de degré \(n\) de \(A\), sans constante. Les monômes sont d’autant moins importants que leur degré est élevé. L’approximation de degré 0 est la loi de puissance. Celle de degré 1 est retenue par les auteurs pour estimer le nombre d’espèces rencontrées sur la surface \(A\) :

\[\begin{equation} \tag{22.3} \hat{S}^{A} = cA^z e^{-kA}. \end{equation}\]

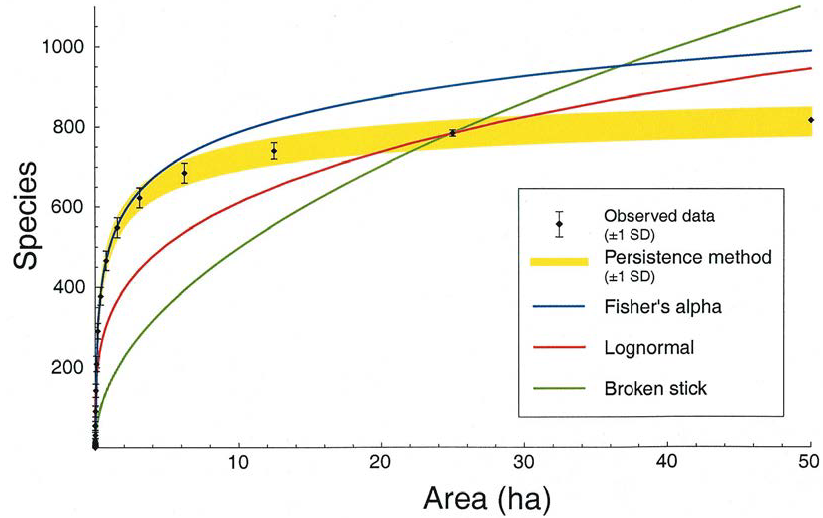
Figure 22.4: Performance du modèle de Plotkin face à des distributions théoriques : SAD log-normales, modèles de Fisher et Broken Stick de MacArthur. La courbe représente le nombre d’espèces rencontrées à Pasoh sur des surfaces de 0 à 50 ha. Les données observées sont des tirages aléatoires d’échantillons de la surface souhaitée. L’écart-type est représenté (l’intervalle de fluctuation à 95 % est de l’ordre de 2 écart-types). Les valeurs issues du modèle ont été obtenues par un paramétrage de \(k\) et \(z\) sur 25 ha, supposé valide également sur les autres forêts. Le paramétrage de \(c\) est obtenu par un échantillon d’un hectare, répété 1000 fois pour obtenir un intervalle de confiance. L’intervalle de fluctuation à 95 % est ici encore de l’ordre de deux écart-types.

Ce modèle contient un paramètre \(k\) en plus de la loi de puissance. Les auteurs ont établi que les paramètres \(k\) et \(z\) étaient très proches pour les cinq forêts (\(z=0,125\) et \(k=0,0541\) à Pasoh), et que leur estimation sur une forêt permettait de prédire avec une très bonne précision la richesse des autres, à partir d’un échantillon d’un hectare nécessaire pour obtenir le paramètre \(c\). La figure 22.4 compare les performances de cette méthode (persistence method), de la loi de puissance 0,25 (loi log-normale) et du modèle de Fisher.

22.2 Le modèle de Gleason

Gleason (1922) réfute le travail d’Arrhenius (1921) à partir de l’argument selon lequel le nombre d’espèces doit se stabiliser quand la surface augmente, au risque de prévoir une richesse beaucoup trop élevée pour de grandes surfaces. Les travaux ultérieurs lui donneront tort (Williamson, Gaston, et Lonsdale 2001).

Gleason propose une relation dans laquelle le nombre d’espèces (et non son logarithme) croît avec le logarithme de la surface :

\[\begin{equation} \tag{22.4} S^{A} = \ln{c} + z \ln{A}. \end{equation}\]

C. B. Williams (1964) reprend ce modèle et affirme sa validité à partir d’arguments sur la variabilité de l’habitat quand la surface d’échantillonnage augmente (par opposition à la relation d’Arrhenius applicable dans un habitat homogène, et due à la distribution log-normale des espèces selon Preston). Connor et McCoy (1979) discutent de la façon de tester les deux hypothèses mais ne disposent pas des données pour le faire.

22.3 Le modèle de placement aléatoire

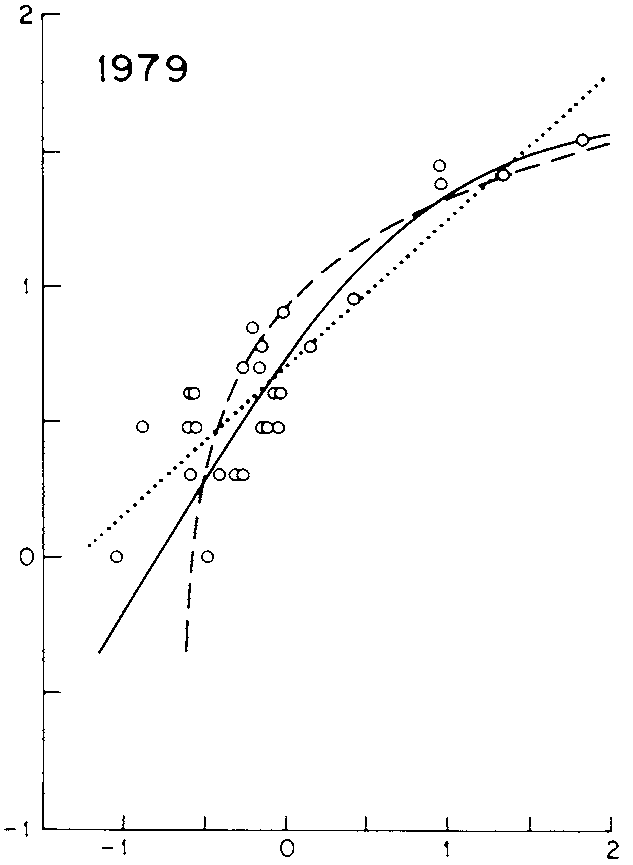
Figure 22.5: Relation aire-espèce de Coleman. Les axes sont en échelle logarithmique. Les points représentent des relevés de nombre d’espèces d’oiseaux (en 1979) en fonction de la taille des îles où elles se trouvaient. La ligne en pointillés courts est l’ajustement d’une loi de puissance (modèle d’Arrhenius). Les pointillés long correspondent du modèle de Gleason. La courbe continue est l’ajustement du modèle de placement aléatoire. Un test de qualité d’ajustement montre que le modèle de placement aléatoire est le plus proche des données.

En concurrence au modèle de Preston (1962) prédisant une SAR en forme de loi de puissance, Coleman (1981; 1982) propose le modèle de placement aléatoire (random placement). L’idée sous-jacente est que certaines communautés ont une composition “aléatoire”, c’est-à-dire issues d’un simple échantillonnage de la méta-communauté. Coleman ne prétend pas que la SAR des arbres de forêt tropicale suive son modèle, mais que ce soit le cas par exemple pour les oiseaux à une échelle spatiale limitée.

Plusieurs îles (communautés locales) de taille relative \(p_i\) appartiennent à un ensemble (méta-communautés) dans lequel la distribution des espèces \(\mathbf{n}\), est considéré comme connue. Chaque individu d’une espèce donnée peut se placer sur une quelconque des îles, avec une probabilité égale à \(p_i\). La probabilité qu’un individu au moins de l’espèce \(s\) se trouve sur l’île \(i\) est \(1-(1-p_i)^{n_s}\) (1 moins la probabilité que tous les individus de l’espèce se trouve sur une autre île, elle-même égale à \(1-p_i\) pour tous les individus). L’espérance du nombre d’espèces représentées sur l’île \(i\) est donc \[\begin{equation} \tag{22.5} {\mathbb E}\left( S^{i}_{\ne 0}\right) = S - \sum_{s}{\left( 1- p_i \right)^{n_s}}. \end{equation}\]

Ce modèle ne fait aucune hypothèse sur la distribution de la probabilité des espèces et n’assume que l’indépendance des individus et la proportionnalité entre la probabilité de présence et la surface. Formellement, il s’agit donc d’une courbe d’accumulation d’espèces. Sur des données de richesse en nombre d’espèces d’oiseaux reproducteurs dans les îles d’un lac nord-américain, le modèle s’ajuste mieux que ceux d’Arrhenius et de Gleason (figure 22.5) (Coleman et al. 1982, fig. 3).

Le modèle de Coleman est parfois utilisé à l’échelle locale, pour construire une courbe d’accumulation par raréfaction (Coleman 1981). \(S\) est alors la richesse de la communauté et \(p_i\) la proportion de la surface de la communauté inventoriée. La courbe est tracée pour les valeurs de \(p-i\) entre 0 et 1. La fonction specaccum de vegan permet de calculer une SAC selon ce modèle.

22.4 Synthèse

La relation d’Arrhenius est plus robuste que celle de Gleason, selon les résultats empiriques et des considérations théoriques (Gárcia Martín et Goldenfeld 2006), y compris de thermodynamique (Würtz et Annila 2008).

Engen (1974) généralise le modèle de Fisher en autorisant des valeurs négatives du paramètre \(k\) de la loi binomiale négative. Dans le modèle de Fisher, ce paramètre est l’inverse de la variabilité de l’espérance du nombre d’individus observés par espèce, qui tend vers 0 car la variabilité est très grande. Il perd son sens quand il devient négatif mais l’espérance du nombre d’espèces en fonction de la surface a une forme plus générale (Engen 1977) : \[\begin{equation} \tag{22.6} {\mathbb E}\left( S^n \right) = \frac{\alpha}{k} \left[ 1 - \left(\frac{\alpha}{\alpha + n}\right)^k \right]. \end{equation}\]

L’équation (20.4) en est la limite pour \(k \to 0\). Pour \(-1<k<0\), avec \(A\) suffisamment grand, l’équation (22.6) revient à la relation d’Arrhenius, où \(z=-k\). Les deux relations peuvent donc être obtenues à partir du même modèle mathématique dont seul le paramètre \(k\) diffère, mais aucune interprétation biologique sur le choix du paramètre n’est possible.

Empiriquement, il est difficile d’estimer lequel des modèles est le plus adapté aux données : sur 35 jeux de données, Connor et McCoy (1979) montrent que les régressions de \(S\) ou \(\ln S\) en fonction de \(A\) ou \(\ln A\) ont des performances similaires en termes de qualité d’ajustement (\(R^2\)), mais Triantis, Guilhaumon, et Whittaker (2012) valident largement le modèle d’Arrhenius pour des SAR insulaires. Ce résultat est conforme à celui de Dengler (2009) qui a testé 23 types de SAR et conclu que la loi de puissance est le modèle le plus universel.

Preston (1960) argumente en faveur du modèle d’Arrhenius (et en défaveur de celui de Gleason) aux échelles intermédiaires et montre que la courbe aire-espèces est triphasique (figure 22.6). Ce résultat fait maintenant consensus mais pas la délimitation des trois échelles, ni la forme de la relation aux échelles extrêmes. On notera que la partie locale de la courbe est en général une courbe d’accumulation, alors que les zones B et C sont traitées comme des SAR au sens strict.

Stephen P. Hubbell (2001), chapitre 6, établit que le modèle de Fisher est pertinent à l’échelle de la méta-communauté et donc de la communauté locale en absence de limitation de la dispersion (si le taux de migration m vaut 1, la communauté locale est un échantillon de la méta-communauté). Dans ce cas, la SAR a la forme de la courbe de la figure 22.6, zone A, et l’indice \(\alpha\) de Fisher est le bon outil de mesure. Mais la dispersion est limitée, et la distribution de la communauté locale est plus compliquée. McGill (2003) montre qu’une SAD log-normale s’ajuste mieux aux données que le modèle neutre selon les résultats de Hubbell. Volkov et al. (2003) établissent la SAD neutre de façon analytique qui s’ajuste mieux aux données que le modèle log-normal, mais la traduction en SAR n’est pas faite.

Figure 22.6: Relation aire-espèce triphasique (Grilli et al. 2012). Zone B : relation d’Arrhenius.

Le meilleur modèle à l’échelle locale est donc celui de Plotkin, Potts, Yu, et al. (2000), qui réfute à la fois Gleason et Arrhenius. La SAC est concave sur une échelle log-log (figure 22.3).

L’utilisation de l’indice \(\alpha\) de Fisher est sujette à caution puisque la SAC locale ne correspond pas au modèle (figure 22.4). Sa valeur calculée plus haut pour BCI est 35, très différente de la valeur de \(\theta\) du modèle neutre pour les mêmes données (Volkov et al. 2003, fig. 1), entre 47 et 50.

L’échelle plus grande (zone B de la figure 22.6) est pour Hubbell un assemblage d’un certain nombre de communautés composant la méta-communauté (page 186). La SAR obtenue par simulation suit la loi de puissance d’Arrhenius. Grilli et al. (2012) développent un modèle de SAR valable à toutes les échelles. Ses hypothèses sont peu réalistes dans la zone A, mais il valide la loi de puissance analytiquement à l’échelle intermédiaire.

La relation d’Arrhenius est donc systématiquement validée à l’échelle régionale (figure 22.1). On remarquera que la distribution de Fisher, validée par Hubbell pour la méta-communauté, n’est jamais observée dans la SAR à cause de l’agrégation spatiale : en augmentant la surface d’échantillonnage, de nouvelles communautés sont ajoutées progressivement, mais l’échantillonnage de toute la méta-communauté n’est jamais réalisé (sauf au point marquant le passage de la zone B à la zone C). Les seuls exemples empiriques sont des inventaires d’arbres à l’échelle de l’Amazonie entière (ter Steege et al. 2013), ou de la totalité des forêts tropicales (Slik et al. 2015) qui correspondent à la distribution de Fisher. Dans ces deux exemples, l’ajustement est obtenu en extrapolant linéairement la SAD, ce qui est légitime (Izsák et Pavoine 2012) si la distribution est effectivement celle de Fisher : la forme de la distribution est donc assumée, pas prouvée. Les valeurs de \(\alpha\) à ces échelles sont bien supérieures aux valeurs locales (35 pour BCI, voir chapitre 20) : 754 pour l’Amazonie, de l’ordre de 1000 pour les néotropiques, mais seulement de 250 pour l’Afrique, et de l’ordre de 2000 pour l’ensemble des tropiques.

Enfin, quand l’échelle est encore plus grande, le nombre d’espèces augmente à nouveau plus vite parce que d’autres méta-communautés sont intégrées.

22.5 Estimation de la richesse à partir de placettes distantes

Krishnamani, Kumar, et Harte (2004), d’après Harte, Kinzig, et Green (1999), développent une méthode permettant l’extrapolation de la richesse mesurée sur de petites surfaces (48 placettes de 0.25 ha) à de très grandes zones (60000 km², la taille des Western Ghats en Inde).

Partant de la relation d’Arrhenius vue précédemment, le nombre d’espèces dans une surface \(A_1\) est

\[\begin{equation} \tag{22.7} S^{A_1} = \left({A_1}/{A_0}\right)^z{S^{A_0}}, \end{equation}\]

c’est-à-dire le nombre d’espèces dans la surface \(A_0\) plus petite multipliée par le rapport des surfaces à la puissance \(z\). La valeur de \(z\) est constante pour des variations de surface limitées. L’idée est donc de procéder par étapes, en partant du nombre d’espèces mesuré sur les petites placettes, et extrapolant vers une surface plus grande. Cette surface est ensuite prise pour référence pour une nouvelle extrapolation avec une nouvelle valeur de \(z\). En indiçant les surfaces de 0 à \(n\), on obtient

\[\begin{equation} \tag{22.8} S^{A_n} = {\left({A_n}/{A_{n-1}}\right)}^{z_{n-1}}{\left({A_{n-1}}/{A_{n -2}}\right)}^{z_{n-2}} \dots{\left({A_1}/{A_0}\right)}^{z_0}S^{A_0}. \end{equation}\]

Il reste à évaluer les différentes valeurs de \(z\). À l’intérieur de chaque placette, l’équation (22.7) est suffisante. À plus grande distance, les auteurs utilisent l’indice de Sørensen, c’est-à-dire deux fois la fraction d’espèces communes entre deux placettes : \(\chi=2{\left(S^{1} \cap S^{2}\right)}/{\left(S^{1}+S^{2}\right)}\). L’indice dépend principalement de la surface des placettes \(A\) et de leur éloignement \(d\). Pour chaque plage de distances, à conditions que les placettes soient éloignées (\(d\) étant la distance entre deux placettes, \({A} \ll d^2\)), \(\chi\) est proportionnel à \(({A}/{d^2})^z\). La valeur de \(z\) peut donc être calculée en comptant le nombre d’espèces communes entre chaque paire de placettes, et ajustant \(\ln\chi\) à \(\ln({A}/{d^2})\) sur des plages de distances convenables pour que \(z\) reste constant, et donc que la relation soit linéaire.

Cette méthode permet l’extrapolation à de très grandes surfaces de mesures de richesse faites sur de petites placettes à condition qu’elles soient assez nombreuses et éloignées les unes des autres.